ВОПРОСЫ К ЭКЗАМЕНУ ПО ДИФФЕРЕНЦИАЛЬНЫМ УРАВНЕНИЯМ

1.Основные понятия и факты, связанные с д.У.

ОДУ порядка n, где n _N, называется уравнение вида

х – независимая переменная.

у – зависимая переменная.

у=у(х) – искомая функция.

y', y′′, …, 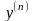- gпроизводные искомой функции.

F – заданная функция.

Порядок уравнения – порядок старшей производной, которая присутствует в уравнении.

Дифференциальное уравнение -го порядка ― лишь бы была (а все остальное может отсутствовать)

Решить: найти все решения (либо доказать, что их нет).

Решение ― объект, который при подстановке обращает уравнение в истинное

График любого решения ДУ – интегральная кривая 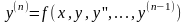- уравнение, разрешенное относительно старшей производной.

у'=f(x,y) – (2) – уравнение первого порядка разрешённое относительно производной.

Решение дифференциального уравнения получено в квадратурах, если оно выражено через элементарные функции посредством конечного числа арифметических операций, операций образования сложной функции и несобственных интегралов, при этом решение может быть функцией, заданной явно, неявно, параметрически, а неопределенные интегралы могут быть неберущимися.

(обычно решить ― решить в квадратурах)

Для решения в квадратурах менять ролями переменные в дифференциальных уравнениях можно (получается неявная функция)

Определение: Начальное условие для уравнения 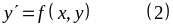следующее дополнительное условие для его решения: 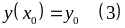, где 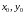―заданные числа

2.Существование,единственность и приближённое решение задачи Коши.

, -задача коши(решить дифференциальные уравнения с начальными условиями).

Наиболее типично: у задачи Коши единственное решение (но не всегда).

Теорема: Пусть в прямоугольнике является непрерывной функцией .

Пусть , где такое дифференциальное уравнение, что 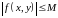. Тогда по меньшей мере на отрезке единственное решение задачи Коши.

формулы для приближенного решения задачи Коши (в общем случае точной формулы не существует):

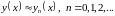
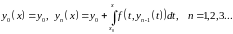
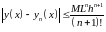, где 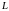―такое число, для которого в прямоугольнике П .

.

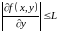3. Д.У.,описывающие физические процессы (радиоактивный распад, гармонические колебания, падение тела и др.)

Задача о радиоактивном распаде.

―время, ―масса вещества. .

Задача о гармонических колебаниях

4.Приближенное построение интегральных кривых с помощью изоклин.

Графики решений дифференциального у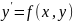равнения называются его интегральными кривыми. Задача построения интегральной кривой часто решается введением изоклин. Изоклиной называется геометрическое место точек, в которых касательные к искомым интегральным кривым имеют одно и тоже направление. Семейство изоклин дифференциального уравнения определяется уравнением f(x,y)=k, где k — параметр. Придавая параметру близкие числовые значения, получаем достаточно густую сеть изоклин, с помощью которых можно приближенно построить интегральные кривые дифференциального yравнения .

5.Уравнения с разделяющимися переменными и уравнения, сводящиеся к ним.

1. уравнение с разделенными переменными:

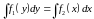
2. уравнение с разделяющимися переменными:

(следить за пропажей корней)

3. уравнение вида

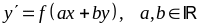
―новая функция, зависящая от

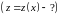
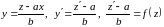
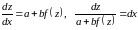
4) однородное уравнение: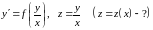

5) уравнение вида .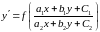

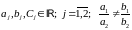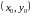единственное решение: ―решение (*)???

.
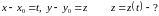
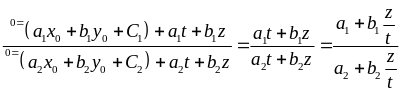