
- •4 Сравнение бесконечно малых функций
- •6.Непрерывность функции в точке
- •13.Основные теоремы дифференциального исчисления. Теоремы Ролля, Лагранжа и Коши.
- •15. Достаточные условия экстремума функции одной переменной. Экстремум функции – это ее локальный максимум или минимум.
- •16.Необходимое условие экстремума функции одной переменной.
- •17. Нахождение асимптот графика функции одной переменной.
1.Обратная матрица. Обратная матрица к исходной матрице А называется матрица А-1, удовлетворяющая условию A*A- 1=A- 1A=E.
ТЕОРЕМА о существовании обратной матрицы. Для того, чтобы квадратная матрица А имела обратную матрицу, необходимо и достаточно (<=>), чтобы матрица А была невыражденной — detA<>0; 1. необходимые условия. Дано: А, А-1; Док-ть: detA¹0; Док-во: Предположим detA=0; AA-1=E; |AA- 1| = |A| |A-1| = |E| = 1; |AA- 1| =0; Противоречие, значит |A|¹0; 2. достаточные условия: Дано A, detA¹0; Док-ть: A-1-?; Док-во: AA-1=E -?; A(a11, a12…a32, A33); Заменим каждый элемент алгебраическим дополнением. В = (A11, A12…A32, A33)*1/|A|; Транспонируем и разделим все элементы на Δ: BT= (A11/Δ, A21/Δ…A23/Δ, A33/Δ); BT=A-1-?; BTA=E -? (a11 a12…a32 a33)*(A11A12…A32 A33)=(a11A11+a12A12+a13A13/Δ)=(1 0..0 1)=E; a21A11+a22A12+a23A13 = 0; a11A11+a12A12+a13A13=Δ;
2.Векторное произведение — это псевдовектор, перпендикулярный плоскости, построенной по двум сомножителям, являющийся результатом бинарной операции «векторное умножение» над векторами в трёхмерном Евклидовом пространстве. Произведение не является ни коммутативным, ни ассоциативным (оно является антикоммутативным) и отличается от скалярного произведения векторов. Во многих задачах инженерии и физики нужно иметь возможность ст
Векторным произведением вектора a на вектор b в пространстве R^3 называется вектор C , удовлетворяющий следующим требованиям:c=a*b*sinFi
длина вектора равна произведению длин векторов и на синус угла ; между ними.
вектор C ортогонален каждому из векторов A и B
вектор C направлен так, что тройка векторов ABC является правой.
в случае пространства R^7 требуется ассоциативность тройки векторов a,b,c.
Обозначение (a*B)= (a,b)=a*b
Выражение векторного произведения через координаты векторов
Пусть в пространстве задан ортонормированный (стандартный) базис I,j,k. Векторные произведения базисных векторов находятся по определению:
![]()
Формулы (1.14) можно получить, используя диаграмму (рис. 1.45): если на этой схеме кратчайший поворот от первого множителя ко второму совершается в положительном направлении (указанном стрелкой), то произведение равно третьему вектору, а если — в отрицательном направлении, то произведение равно третьему вектору, взятому со знаком минус (противоположному вектору).
Найдем
выражение векторного произведения
через координаты множителей. Пусть в
стандартном базисе I,j,k
векторы a
и b
имеют координаты
![]() и
и
![]() соответственно. Тогда, используя
линейность векторного произведения
по любому множителю (см. пункт 2 замечаний
1.12) и формулы (1.14), получаем
соответственно. Тогда, используя
линейность векторного произведения
по любому множителю (см. пункт 2 замечаний
1.12) и формулы (1.14), получаем
![]()
Запишем
это равенство при помощи определителей
второго порядка:
![]()
Правую часть (1.15) можно представить как результат разложения символического определителя третьего порядка по первой строке
![]()
Теорема 1.8 (формула вычисления векторного произведения). Если векторы a и b в правом ортонормированием базисе I,j,k имеют координаты и соответственно, то векторное произведение этих векторов находится по формуле, которую принято записывать в виде
![]()
Если
![]() и
и
![]() — координатные столбцы векторов a
и b
в стандартном базисе, то координатный
столбец
— координатные столбцы векторов a
и b
в стандартном базисе, то координатный
столбец
![]() векторного произведения
векторного произведения
![]() находится по формуле
находится по формуле
![]()
В
самом деле, выполняя умножение матрицы
на столбец, получаем![]()
Тогда
,
![]() что совпадает с (1.15).
что совпадает с (1.15).
3. Кривая второго порядка — геометрическое место точек, декартовы прямоугольные координаты которых удовлетворяют уравнению вида
![]()
в котором по крайней мере один из коэффициентов A11,А12,А22 отличен от нуля.
Гипербола — геометрическое место точек M Евклидовой плоскости, для которых абсолютное значение разности расстояний от M до двух выделенных точек F1 и F2 (называемых фокусами) постоянно.
Декартовы координаты
Гипербола задаётся уравнением второй степени в декартовых координатах (x, y) на плоскости:
![]()
где коэффициенты Axx, Axy, Ayy, Bx, By, и C удовлетворяют следующему соотношению
![]()
и
![]()
Эллипс— геометрическое место точек M Евклидовой плоскости, для которых сумма расстояний до двух данных точек F1 и F2 (называемых фокусами) постоянна и больше расстояния между фокусами, то есть| F1M | + | F2M | = 2a, причем | F1F2 | < 2a.
Эллипс является центральной невырожденной кривой второго порядка и удовлетворяет общему уравнению вида
при
инвариантах
![]() и
и
![]() где:
где:
![]()
![]()
![]()
Соотношения между инвариантами кривой второго порядка и полуосями эллипса:
![]()
![]()
![]()
4 Сравнение бесконечно малых функций
Пусть при x→a функции f(x) и g(x) являются бесконечно малыми. Тогда будем пользоваться следующими определениями.
Если
 ,
то f(x)
называется бесконечно
малой высшего порядка,
чем g(x)
(относительно g(x)).
,
то f(x)
называется бесконечно
малой высшего порядка,
чем g(x)
(относительно g(x)).Если
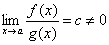 ,
то функции f(x)
и g(x)
называются бесконечно
малыми одногопорядка.
,
то функции f(x)
и g(x)
называются бесконечно
малыми одногопорядка.Если
 ,
то f(x)
называется бесконечно
малой k-го порядка относительноg(x).
,
то f(x)
называется бесконечно
малой k-го порядка относительноg(x).
Если
![]() ,
то функции f(x)
и g(x)
называются эквивалентными
бесконечно
малыми.
В этом случае обе функции стремятся к
нулю примерно с одинаковой скоростью.
Эквивалентные бесконечно малые будем
обозначать f
≈ g.
,
то функции f(x)
и g(x)
называются эквивалентными
бесконечно
малыми.
В этом случае обе функции стремятся к
нулю примерно с одинаковой скоростью.
Эквивалентные бесконечно малые будем
обозначать f
≈ g.
5.
Таблица эквивалентно малых функций, с
доказательством каждой из них. Поскольку
в этой таблице мы всегда будем
рассматривать базу
![]() ,
для простоты записи обозначение этой
базы будем пропускать и писать знак
,
для простоты записи обозначение этой
базы будем пропускать и писать знак
![]() вместо
вместо
![]() . !1)
. !1)
![]() . Эту формулу мы уже доказали и использовали
в примерах. Эквивалентность sinx
и x
при
означает в точности, что первый
замечательный предел равен 1.
. Эту формулу мы уже доказали и использовали
в примерах. Эквивалентность sinx
и x
при
означает в точности, что первый
замечательный предел равен 1.
!2)
![]() . Эта эквивалентность тоже была доказана
выше в одном из примеров.
. Эта эквивалентность тоже была доказана
выше в одном из примеров.
3)
![]() .
Докажем эту эквивалентность:
.
Докажем эту эквивалентность:
![]()
!4)
![]() . Докажите это в качестве упражнения,
сделав замену
. Докажите это в качестве упражнения,
сделав замену
![]() и применив предыдущую табличную формулу.
и применив предыдущую табличную формулу.
!5
![]() )
. Для доказательства воспользуемся
формулой
)
. Для доказательства воспользуемся
формулой
![]() .
Далее, имеем:
.
Далее, имеем:
![]()
Это означает, что доказываемая эквивалентность имеет место.
6)
![]() . Для доказательства этой эквивалентности
сделаем такое преобразование:
. Для доказательства этой эквивалентности
сделаем такое преобразование:
![]()
Для вычисления предела правой части воспользуемся непрерывностью логарифма и вторым замечательным пределом:
![]()
и мы доказали формулу 6.
В частном случае, при a=e , получаем эквивалентность
6)![]()
7)
![]() ( ). Для доказательства сделаем замену
( ). Для доказательства сделаем замену
![]() и выразим x
через z
:
и выразим x
через z
:
![]() .Согласно
формуле 6, при
, откуда
.Согласно
формуле 6, при
, откуда
![]() . Из непрерывности логарифма следует,
что
. Из непрерывности логарифма следует,
что
![]() и, значит,
и, значит,
![]() при
при
![]() . В этой формуле осталось лишь сменить
обозначение переменного z
на x
, чтобы получить формулу 7.
. В этой формуле осталось лишь сменить
обозначение переменного z
на x
, чтобы получить формулу 7.
В частном случае, при a=e , получаем эквивалентность
!7)![]()
Сведём теперь полученные формулы в итоговую таблицу. Всюду в ней . 1) .
sin α(x) ~ α(x) 1 − cos α(x) ~ α(x)2/2 |
tg α(x) ~ α(x) arcsin α(x) ~ α(x) |
arctg α(x) ~ α(x) eA(X) − 1 ~ α(x) |
a A(X) − 1 ~ α(x) · ln a ln[1 + α(x)] ~ α(x) |
LOG a[1 + α(x)] ~ α(x)/ln a |
[1 + α(x)]M − 1 ~ mα(x |
6.Непрерывность функции в точке
Пусть функция f(x) определена в некоторой окрестности O(x0) точки x0 (включая саму точку x0). Функция f(x) называется непрерывной в точке x0, если существует limx → x0 f(x) , равный значению функции f(x) в этой точке:
|
f(x) = f(x0),
Классификация точек разрыва функции Все
точки разрыва функции разделяются
на точки
разрыва первого и второго рода.
Говорят, что функция f
(x)
имеет точку
разрыва первого рода
при x
= a,
если в это точке Существуют левосторонний
предел и правосторонний предел
При
этом возможно следующие два случая:
Левосторонний предел и правосторонний
предел равны друг другу:
Функция f (x) имеет точку разрыва второго рода при x = a, если по крайней мере один из односторонних пределов не существует или равен бесконечности.
|
7.Произво́дная (функции в точке) — основное понятие дифференциального исчисления, характеризующее скорость изменения функции (в данной точке). Определяется как предел отношения приращения функции к приращению ее аргумента при стремлении приращения аргумента к нулю, если такой предел существует.
2)
Геометрический смысл производной:
производная
в т.х0 равна угловому коэф-ту касательной
к графику ф-и y=f(x) в этой точке f'(x0)=k.
3)
Механический
смысл производной:
производная от координаты по времени
есть скорость v(t)=x'(t).
9
Логарифмическая
производная –
производная от натурального логарифма
модуля (абсолютной величины) – данной
функции:
![]()
Используя
формулу производной сложной функции,
найдем, что
![]() (*)Логарифмическую
производную используют, например, при
дифференцировании (нахождении производной
или дифференциала) степенно-показательной
функции
(*)Логарифмическую
производную используют, например, при
дифференцировании (нахождении производной
или дифференциала) степенно-показательной
функции
10.Производная
обратной функции. Производные обратных
тригонометрических функций (с выводом).
Пусть
![]() -
дифференцируемая
функция
от аргумента x в некотором интервале
-
дифференцируемая
функция
от аргумента x в некотором интервале
![]() .
Если в уравнении
y
считать аргументом, а x - функцией, то
возникает новая функция
.
Если в уравнении
y
считать аргументом, а x - функцией, то
возникает новая функция
![]() ,
где
,
где
![]() -
функция
обратная данной.
-
функция
обратная данной.
![]()
![]()
![]()
![]()
![]()
![]()
11.
Формула
Тейлора Пусть
функция f(x)
имеет n
+ 1 производную
в некоторой окрестности
точки
a,
![]()
Пусть
![]()
Пусть p — произвольное положительное число,
тогда:
![]() точка
точка
![]() при
x
< a
или
при
x
< a
или
![]() при
x
> a:
при
x
> a:
![]()

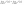 Такая
точка называется точкой
устранимого разрыва.
Левосторонний предел и правосторонний
предел не равны друг другу:
Такая
точка называется точкой
устранимого разрыва.
Левосторонний предел и правосторонний
предел не равны друг другу:
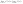 Такая точка называется точкой
конечного разрыва.
Модуль разности значений односторонних
пределов
Такая точка называется точкой
конечного разрыва.
Модуль разности значений односторонних
пределов