21. Центральная предельная теорема и особая роль нормального распределения. Формулы для практического применения теории вероятностей (интегральная теорема Муавра-Лапласа).

Предельные законы распределения составляют предмет группы теорем под названием «Центральная предельная теорема», которую иногда называют «количественной формой закона больших чисел». Все формы ЦПТ посвящены установлению условий, при которых возникает НЗР. Так как эти условия на практике весьма часто выполняются, НЗР является самым распространенным из законов распределения, наиболее часто встречающимся в случайных явлениях природы. Он возникает во всех случаях, когда исследуемая СВ м.б. представлена в виде сумма достаточно большого числа независимых (или слабо зависимых) элементарных слагаемых, каждое из которых в отдельности сравнительно мало влияет на сумму.

Наиболее простой формой ЦПТ является следующая:

Если Х1, Х2, …, Хn – независимые СВ, имеющие один и тот же закон распределения с матожиданием m и дисперсией σ², то при неограниченном увеличении n закон распределения суммы Y_n=Σⁿ_k=1X_k неограниченное приближается к нормальному.

Центральная предельная теорема – если СВ Х представляет собой сумму очень большого числа взаимно независимых случайных величин, влияние каждой из которых на всю сумму ничтожно мало, то Х имеет распределение, близкое к нормальному.

Теорема Ляпунова. Если X₁,…, X_n - независимые СВ, у каждой из которых существует M(X_i)=а, D(X_i)=σ², абсолютный центральный момент третьего порядка M(|X_i-a_i|³)=m_i и 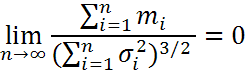, то закон распределения суммы Y_n= X₁+…+ X_n при n→∞ неограниченно приближается к нормальному с матожиданием и дисперсией .

В практических задачах часто применяют ЦПТ для вычисления вероятности того, что сумма нескольких СВ окажется в заданных пределах.

Пусть X1, X2, …, Xn – независимые СВ с матожиданиями m₁, … m_n, и дисперсиями D₁,… D_n, . Предположим, что условия ЦПТ выполнены (величины X1, X2, …, Xn сравнимы по порядку своего влияния на рассеивание суммы) и число слагаемых n достаточно для того, чтобы закон распределения величины Y_n=Σⁿ_k=1X_k можно было бы считать нормальным.

Тогда вер-ть того, что СВ У попадет в пределы участка (α;β):

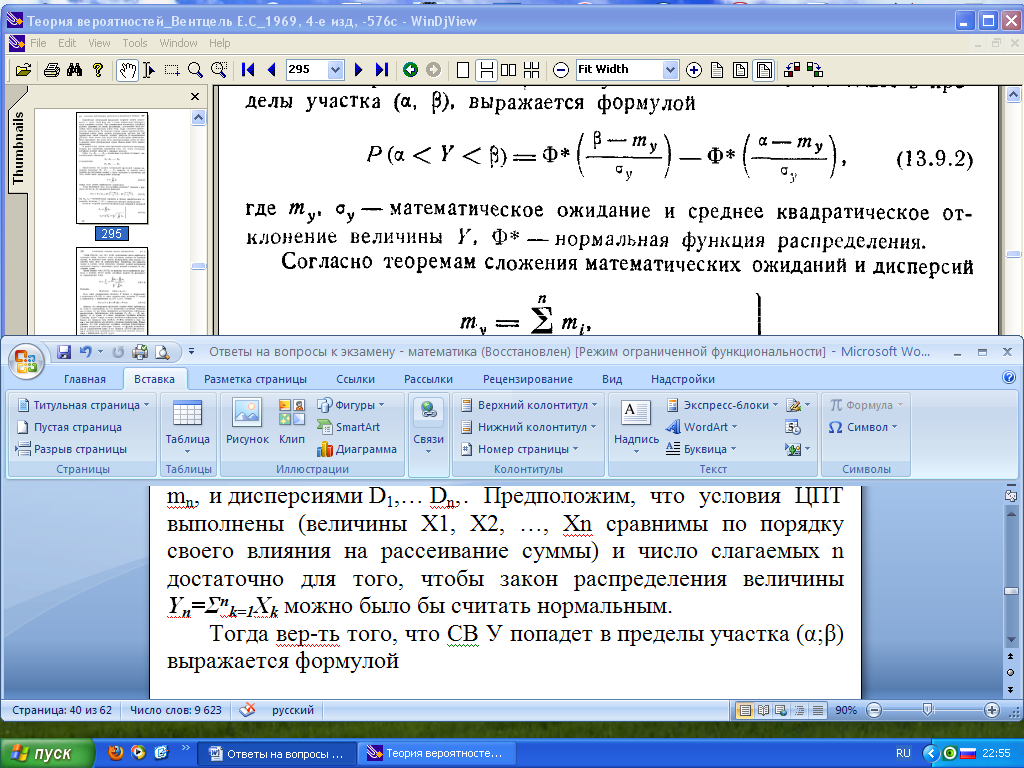
Таким образом, для того, чтобы приближенно найти вероятность попадания суммы большого числа СВ на заданный участок, не требуется знать законы распределения этих величин; достаточно знать лишь их характеристики. Разумеется, это относится только к случаю, когда выполнено основное условие ЦПТ – равномерно малое влияние слагаемых на рассеивание суммы.

Частный случаем ЦПТ для дискретных СВ – теорема Лапласа:

Если производится n независимых опытов, в каждом из которых событие А появляется с вероятностью p, то справедливо соотношение:

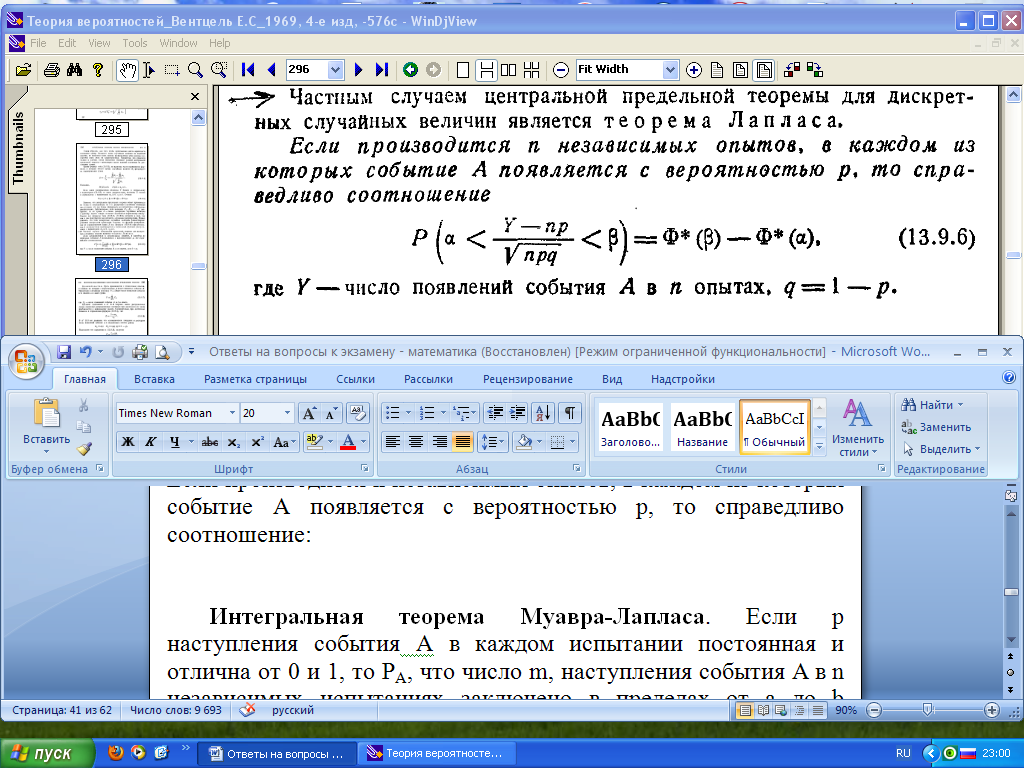
Где Y – число появлений события А в n опытах, q=1-p.

Интегральная теорема Муавра-Лапласа. Если p наступления события А в каждом испытании постоянная и отлична от 0 и 1, то Р_А, что число m, наступления события А в n независимых испытаниях заключено в пределах от a до b (включительно), при достаточно большом числе n прибл. равна:

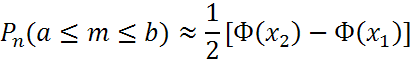
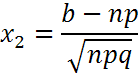
, где 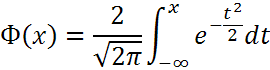– функция (или интеграл вероятностей) Лапласа;

Вышеуказанная формула – ф-ла Муавра-Лапласа. Чем больше n, тем она точнее. При выполнении условия npq≥20 она дает, как правило, удовл-ю для практики погрешность вычисления вер-тей.

Свойства функции:

1. Ф(х) – четная, т.е. Ф(-х)=Ф(х)

2. Ф(х) – монотонно возрастающая, причем при х→+∞ Ф(х)→1 (практически можно считать, что уже при x>4 Ф(х)~4)

Следствие интегральной теоремы Муавра-Лапласа:

Если p наступления события А в каждом испытании постоянна и отлична от 0 и 1, то при достаточно большом числе n независимых испытаний Р_а, что:

а) число m наступлений события А отличается от произведения np не более, чем на величину ε>0 (по абсолютной величине), т.е.

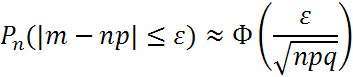
б) частость m/n события А заключается в пределах от α до β (вкл)

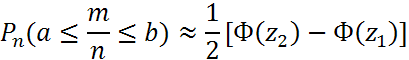, где

в) частость m/n события А отличается от его p не более, чем на величину ∆>0 (по абс. величине):