45. Градієнтні методи розв’язання задач нелінійного програмування. Метод Франка-Вульфа розв’язування задачі нелінійного програмування. Навести відповідні формули.

Градієнтні методи належать до наближених методів розв’язування задач нелінійного програмування і дають лише пев­не наближення до екстремуму, причому за збільшення обсягу обчислень можна досягти результату з наперед заданою точністю, але в цьому разі є можливість знаходити лише локальні екстремуми цільової функції. Зауважимо, що такі методи можуть бути застосовані лише до тих типів задач нелінійного програмування, де цільова функція і обмеження є диференційовними хоча б один раз. Зрозуміло, що градієнтні методи дають змогу знаходити точки глобального екстремуму тільки для задач опуклого програмування, де локальний і глобальний екстремуми збігаються.

В основі градієнтних методів лежить основна властивість градієнта диференційовної функції – визначати напрям найшвидшого зростання цієї функції. Ідея методу полягає у переході від однієї точки до іншої в напрямку градієнта з деяким наперед заданим кроком.

Розглянемо метод Франка-Вульфа, процедура якого передбачає визначення оптимального плану задачі шляхом перебору розв’язків, які є допустимими планами задачі.

Нехай необхідно відшукати

за лінійних обмежень:

;

Допустимо, що Х₀ – початкова точка, що належить множині допустимих планів даної задачі. В деякому околі цієї точки нелінійну цільову функцію замінюють лінійною і потім розв’язують задачу лінійного програмування. Нехай розв’язок лінійної задачі дав значення цільової функції F₀, тоді з точки Х₀ в напрямку F₀ необхідно рухатись доти, поки не припиниться зростання цільової функції. Тобто у зазначеному напрямку вибирають наступну точку Х₁, цільова функція знову замінюється на лінійну, і знову розв’язується задача лінійного програмування.

Розглянемо детальніше перехід від k-ої ітерації методу до (k + 1)-ої ітерації.

Припустимо, що відома точка X_k, яка належить області допустимих розв’язків. У даній точці обчислюємо градієнт цільової функції:

.

Значення градієнта функції задає в даній точці напрям най­швидшого її зростання.

Замінюємо цільову функцію задачі лінійною функцією виду:

.

Потім розв’язуємо задачу лінійного програмування з обмеженнями початкової задачі і новою цільовою функцією:

за умов:

;

.

Нехай розв’язком такої задачі є точка .

З початкової точки в напрямку рухаємося з деяким довільним кроком , визначаючи координати нової точки у такий спосіб:

Зауважимо, що значення параметра доцільно вибирати таким, що дає найбільше значення цільової функції початкової задачі .

Для точки Х_k+1 повторюємо розглянутий процес, для чого знову розраховуємо значення градієнта і т. д.

У такий спосіб знаходимо послідовність точок , які поступово наближаються до оптимального плану початкової задачі. Ітераційний процес повторюється до того моменту, поки значення градієнта цільової функції не стане рівним нулю або виконуватиметься умова 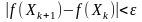, де – досить мале число, яке означає потрібну точність обчислень.