
- •1. Сутність поняття “модель”. Особливості математичної моделі.
- •3. Особливості і принципи математичного моделювання. Узагальнена схема математичного моделювання.
- •4. Поняття економіко-математичної моделі. Узагальнена схема процесу математичного моделювання економічних процесів. Особливості процесу математичного моделювання економічних систем.
- •5. Особливості економічних спостережень і вимірів.
- •6. Охарактеризуйте основні етапи економіко-математичного моделювання.
- •7. Сутність адекватності економіко-математичних моделей. Перевірка адекватності моделі.
- •8. Основні засади щодо класифікації економіко-математичних моделей. Наведіть приклади та дайте відповідні пояснення.
- •9. Сутність аналітичного та комп’ютерного моделювання.
- •10. Роль прикладних економіко-математичних досліджень.
- •11. «Павутиноподібна» модель. Гіпотези, що приймаються в моделі.
- •12. Стійка рівновага у «павутиноподібній» моделі. Умови існування стійкої рівноваги у «павутиноподібній» моделі.
- •13. Постановка задачі економіко-математичного моделювання. Сутність понять: «параметри», «змінні», «цільова функція», «система обмежень», «оптимальний план».
- •14. Предмет математичного програмування. Приклади економічних задач математичного програмування.
- •15. Багатокритеріальна оптимізація економічних систем.
- •16. Классифікація задач математичного програмування.
- •17. Загальна постановка задачі лінійного програмування. Приклади економічних задач лінійного програмування.
- •18. Форми запису задачі лінійного програмування, охарактеризувати їх. Навести відповідні формули.
- •19. Геометрична інтерпретація задач лінійного програмування. Властивості розв’язків задачі лінійного програмування.
- •Перехід від одного опорного плану до іншого
- •21. Алгоритм графічного методу розв’язування задач лінійного програмування.
- •23. 24. Умова оптимальності розв’язку задачі лінійного програмування симплекс-методом. Алгоритм симплексного методу. Навести відповідні формули.
- •25. Метод штучного базису. Ознака оптимальності плану із штучним базисом.
- •26. Двоїста задача. Правила побудови двоїстої задачі. Симетричні й несиметричні двоїсті задачі. Навести відповідні формули.
- •27. Економічний зміст двоїстої задачі й двоїстих оцінок.
- •28. Теореми двоїстості, їх економічна інтерпретація.
- •29. Застосування теорем двоїстості в розв’язуванні задач лінійного програмування. Навести відповідні формули.
- •30. Цілочислове програмування. Приклади застосування цілочислових задач в плануванні й управлінні виробництвом. Навести відповідні формули.
- •31. Геометрична інтерпретація задачі цілочислового програмування.
- •32. Загальна характеристика методів розв’язування задач цілочислового програмування.
- •33. Сутність цілочислового програмування. Графічний метод розв’язування задач цілочислового програмування.
- •34. Методи відтинання. Метод Гоморі. Навести відповідні формули.
- •35. Комбінаторні методи. Метод гілок і меж. Навести відповідні формули.
- •36. Постановка задачі нелінійного програмування, математична модель. Геометрична інтерпретація.
- •38. Основні труднощі розв’язування задач нелінійного програмування.
- •39. Графічний метод розв’язування задач нелінійного програмування.
- •40.41. Метод множників Лагранжа пошуку умовного екстремуму функції. Визначення типу екстремуму. Навести відповідні формули.
- •42. Алгоритм розв’язування задачі на безумовний екстремум. Визначення типу екстремуму. Навести відповідні формули.
- •43. Поняття про опуклі функції
- •Опуклі й угнуті функції
- •44. Сідлова точка та необхідні умови її існування. Навести відповідні формули.
- •45. Градієнтні методи розв’язання задач нелінійного програмування. Метод Франка-Вульфа розв’язування задачі нелінійного програмування. Навести відповідні формули.
- •46. Постановка зад.Динам.Прогр. Та її геометрична інтерпретація
- •47.Принцип оптимальності та алгоритм динамічного програмування.
- •50.Основні поняття та завдання теорії ігор.
- •52.Геом.Інтерпретація гри 2х2
- •54. Зведення матричної гри до задачі лінійного програмування.
39. Графічний метод розв’язування задач нелінійного програмування.
Приклад 9.1. Знайти мінімальне і максимальне значення функції:

за умов:

 .
.
Розв’язання. Область допустимих розв’язків утворює чотирикутник АВСD (рис.9.1).
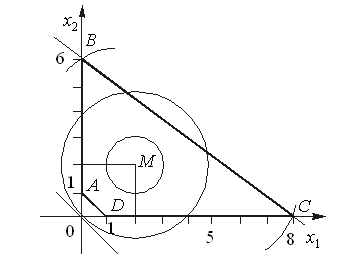
Рисунок 9.1
Геометрично
цільова функція являє собою коло з
центром у точці М(2;2),
квадрат радіуса якого
 .
Це означає, що її значення буде
збільшуватися (зменшуватися) зі
збільшенням (зменшенням) радіуса кола.
Проведемо з точки М
кола різних радіусів. Функція
Z
має два локальних максимуми:
точки В(0;6)
і С(8;0).
Обчислимо значення функціонала в цих
точках:
.
Це означає, що її значення буде
збільшуватися (зменшуватися) зі
збільшенням (зменшенням) радіуса кола.
Проведемо з точки М
кола різних радіусів. Функція
Z
має два локальних максимуми:
точки В(0;6)
і С(8;0).
Обчислимо значення функціонала в цих
точках:
 ,
,
 .
.
Оскільки
 ,
то точка С(8;0) є точкою глобального
максимуму.
,
то точка С(8;0) є точкою глобального
максимуму.
Очевидно, що
найменший радіус
 ,
тоді:
,
тоді:
 .
.
Тобто точка М є точкою мінімуму, оскільки їй відповідає найменше можливе значення цільової функції.
Зазначимо, що в даному разі точка, яка відповідає оптимальному плану задачі (мінімальному значенню функціонала), знаходиться всередині багатокутника допустимих розв’язків, що в задачах лінійного програмування неможливо.
40.41. Метод множників Лагранжа пошуку умовного екстремуму функції. Визначення типу екстремуму. Навести відповідні формули.
Розглянемо метод множників Лагранжа для розв’язування задачі нелінійного програмування, що має вигляд:
 (9.6)
(9.6)
за умов:
 , (9.7)
, (9.7)
де функції
 і
і
 мають бути диференційовними.
мають бути диференційовними.
Задача (9.6)-(9.7)
полягає в знаходженні екстремуму функції
 за умов виконання обмежень
за умов виконання обмежень
 .
.
Переходимо до задачі пошуку безумовного екстремуму. Теоретично доведено, що постановки та розв’язання таких задач еквівалентні.
Замінюємо цільову функцію (9.6) на складнішу. Ця функція називається функцією Лагранжа і має такий вигляд:
 (9.8)
(9.8)
де
 – деякі невідомі величини,
що називаються множниками Лагранжа.
– деякі невідомі величини,
що називаються множниками Лагранжа.
Знайдемо частинні похідні і прирівняємо їх до нуля:

 (9.9)
(9.9)
Друга група рівнянь системи (9.9) забезпечує виконання умов (9.7) початкової задачі нелінійного програмування.
Система (9.9), як правило, нелінійна.
Розв’язками її є
і
 – стаціонарні точки. Оскільки, ці
розв’язки отримані з необхідної умови
екстремуму, то вони визначають максимум,
мінімум задачі (9.6)-(9.7)
або можуть бути точками перегину
(сідловими точками).
– стаціонарні точки. Оскільки, ці
розв’язки отримані з необхідної умови
екстремуму, то вони визначають максимум,
мінімум задачі (9.6)-(9.7)
або можуть бути точками перегину
(сідловими точками).
Для
діагностування стаціонарних точок і
визначення типу екстремуму
необхідно перевірити виконання достатніх
умов екстремуму, тобто дослідити в околі
стаціонарних точок диференціали другого
порядку (якщо для функцій
 існують другі частинні похідні і вони
неперервні).
існують другі частинні похідні і вони
неперервні).
Узагальнення
достатньої умови існування локального
екстремуму для
функції n
змінних приводить до такого правила:
за функцією Лагранжа виду (9.8)
будується матриця Гессе, що має блочну
структуру розмірністю
 :
:

де О –
матриця розмірністю
 ,
що складається з нульових елементів,
,
що складається з нульових елементів,
Р
–
матриця розмірністю
 ,
елементи якої визначаються так:
,
елементи якої визначаються так:
 ,
,
 – транспонована
матриця до Р розмірністю
– транспонована
матриця до Р розмірністю
 ,
,
Q –
матриця розмірністю
 виду:
виду:
 ,
де
,
де
 .
.
Розглянемо ознаки виду екстремуму розв’язку системи (9.9). Нехай стаціонарна точка має координати і .
1. Точка
є точкою максимуму, якщо, починаючи з
головного мінору порядку (m+1),
наступні (n–m) головних мінорів
матриці Н утворюють знакозмінний
числовий ряд, знак першого члена якого
визначається множником
 .
.
2. Точка
є точкою мінімуму, якщо, починаючи з
головного мінору порядку (m+1), знак
наступних (n–m) головних мінорів
матриці Н визначається множником
 .
.
