
- •Билет №1
- •1. Конденсационные методы получения лиофобных дисперсных систем.
- •2. Особенности адсорбции ионов и молекул из растворов на твердой поверхности.
- •3. Реология
- •4. Сравните давление насыщенного пара над одинаковыми по размерам каплями воды и пропилового спирта.
- •5. Изобразите формулы двух мицелл гидрозоля с, полученного из растворов веществ а и в в случае избытка вещества а или в. А - ВеСl2, в - nh4oh, с - Be(oh)2
- •Билет 2
- •1. Диспергационные методы получения лиофобных дисперсных систем.
- •2. Межфазная поверхность, ее силовое поле. Поверхностное натяжение как характеристика этого поля
- •3. Что Вы знаете о структурообразовании в дисперсных системах и типах дисперсных структур?
- •4. Сравните давление насыщенного пара над каплями эквиконцентрированных водных растворов уксусной и масляной кислот (радиусы капель одинаковы). Ответ обоснуйте.
- •5. Изобразите формулы двух мицелл гидрозоля с, полученного из растворов веществ а и в в случае избытка вещества а или в. А: k2CrO4, b: AgNo3, c: Ag2CrO4
- •1. Седиментационный анализ суспензий и эмульсий.
- •2. Поверхностная активность. Экспериментальное определение, изменение в гомологических рядах, работа адсорбции.
- •5. Изобразите формулы двух мицелл гидрозоля с, полученного из растворов веществ а и в в случае избытка вещества а или в. А - Na2 SiO3, в - hCl, с - h2SiO3
- •Билет 4
- •1. Смачивание и растекание:
- •2 Метод избыточных величин Гиббса и метод слоя конечной толщины
- •3. Дайте определение поверхностной активности и поясните выражение «понятие поверхностной активности относительно». Как экспериментально оценить поверхностную активность?
- •5. Изобразите формулы двух мицелл гидрозоля с, полученного из растворов веществ а и в в случае избытка вещества а или в. А (NaCl), в (kh2SbO4), с (NaH2SbO4).
- •Билет 5
- •1. Седиментационный анализ в центробежном поле как метод оценки размеров коллоидных частиц и макромолекул полимеров.
- •2. Адсорбция и ее характеристики. Теории полимолекулярной адсорбции.
- •3. Что такое аэрозоли? Чем обусловлены их специфические свойства и как их разрушают?
- •4. С каким коллоидно-химическим явлением в организме человека связано чувство жажды? Охарактеризуйте это явление и его особенности в коллоидных системах по сравнению с истинными растворами.
- •5. Изобразите формулы двух мицелл гидрозоля с, полученного из растворов веществ а и в в случае избытка вещества а или в. А - CaCl2, в - h2so4, с - CaSo4
- •Билет 6
- •1. Диффузия и ее особенности в коллоидных системах. Уравнение Эйнштейна.
- •2. Лиофильные коллоидные системы. Условия образования и свойства.
- •3. Изобразите изотермы поверхностного натяжения водных растворов метиламина и пропиламина и покажите, как от них можно перейти к изотермам адсорбции. Изобразите изотермы адсорбции этих веществ.
- •4. Как различаются осмотические давления апельсинового сока а) с мякотью, б) без мякоти. Ответ обоснуйте
- •5. Изобразите формулы двух мицелл гидрозоля с, полученного из растворов веществ а и в в случае избытка вещества а или в. А – CaCl2, в - h2so4, с - CaSo4
- •Билет 7
- •1. Изотерма адсорбции Лэнгмюра.
- •2. Устойчивость дисперсных систем. Основы теории длфо.
- •3. Приведите на одном рисунке изотермы поверхностного натяжения пив и пав а)немицеллообразующего , б) мицеллообразующего, в) ионогенного немицеллообразующего.
- •5. Изобразите формулы двух мицелл гидрозоля с, полученного из растворов веществ а и в в случае избытка вещества а или в. А - CaCl2, в - h2so4, с - CaSo4
- •Билет 8.
- •1. Уравнение адсорбции Гиббса и его естественно-научное и философское значение.
- •2. Диффузионно-седиментационное равновесие и его использование для анализа д исперсных систем.
- •5. Изобразите формулы двух мицелл гидрозоля с, полученного из растворов веществ а и в в случае избытка вещества а или в. А - k3(Fe(cn)6), в - AgNo3, с - Ag3(Fe(cn)6)
- •6. Изобразите графически изменение ζ-потенциала для золя MnO2 (стабилизатор Na2s2o3) при добавлении к нему электролитов NaCl, AgNo3, kMnO4, Na2s2o3 .
- •Билет 9.
- •1. Зависимость поверхностного натяжения от концентрации пав. Уравнение Шишковского, физический смысл его констант и методы их определения.
- •2. Образование и строение двойного электрического слоя на границе раздела фаз.
- •3. Что Вы знаете о критических эмульсиях и микроэмульсиях?
- •5. Изобразите формулы двух мицелл гидрозоля с, полученного из рас - творов веществ а и в в случае избытка вещества а или в. А - k2so4, в - Ba(ch3coo)2, с - BaSo4
- •Билет 10.
- •2. Уравнение двухмерного состояния вещества в адсорбционном слое. Основные типы поверхностных пленок.
- •3. Как можно определить важнейшие характеристики молекул пав: площадь поперечного сечения и длину?
- •5. Изобразите формулы двух мицелл гидрозоля с, полученного из растворов веществ а и в в случае избытка вещества а или в. А - Na 2SiO3, в - AgNo3, с - Ag2SiO3
2 Метод избыточных величин Гиббса и метод слоя конечной толщины
Чтобы получить связь между характером распределения плотностей термодинамических функций в поверхности разрыва и макроскопическими характеристиками поверхности и объемных фаз используется два метода: метод избыточных величин Гиббса и метод слоя конечной толщины.
В методе слоя конечной толщины поверхность разрыва рассматривается как реальный слой, который отличается от объемных фаз тем, что обладает избыточной энергией σs. В этом методе вводится параметр толщины поверхностного слоя.
Гиббс предпочел идти по пути более схематичного описания термодинамики поверхностных явлений. В его методе свойства реальной системы сопоставляются со свойствами идеализированной системы, в которой плотности термодинамических величин сохраняют постоянное (объемное) значение вплоть до некоторой математической (имеющей нулевую толщину) разделяющей поверхности. Разность (положительная или отрицательная) между значениями термодинамической функции в реальной системе и системе сравнения, отнесенная к площади поверхности, рассматривается как удельное значение избытка соответствующей величины. Именно эта избыточная величина сопоставляется с соответствующей макроскопической характеристикой. При этом определение такого избытка основывается на интегрировании по координате, нормальной к поверхности, разности плотностей термодинамических функций в реальной системе и системе сравнения. При помощи этих двух методов выразить любой термодинамический параметр системы.
По методу Гиббса (участок I на рисунке):
G = G1 + G2 + σs,
где G1 и G2 – значения энергии Гиббса отдельных фаз в идеализированной системе, соответствующие их объемным значениям, σs – избыток, связанный с разделяющей поверхностью.
По методу слоя конечной толщины (участок II на рисунке):
G = G1′ + G2′ + Gсл = G1′ + G2′ + Gvсл + σs,
где G1′ и G2′ – энергия Гиббса соответственно фазы 1 и 2 до границы поверхностного слоя (поверхности разрыва).
Применительно к дисперсной системе можно записать объединенное уравнение первого и второго начал термодинамики относительно энергии Гиббса:
 ,
,
где S – энтропия; dT, dp – изменение температуры и давления; ds – изменение площади поверхности раздела фаз; σ – поверхностное натяжение; μi, ni – химический потенциал и число моль компонента i; φ, q – электрический потенциал и заряд поверхности.

3. Дайте определение поверхностной активности и поясните выражение «понятие поверхностной активности относительно». Как экспериментально оценить поверхностную активность?
Поверхностная
активность –
способность вещества понижать
поверхностное натяжение данной границы
раздела фаз. Эту способность характеризует
производная
![]() при Т,р=const
которая изменяется с изменением
концентрации. Физический смысл
производной: понижение поверхностного
натяжения раствора при изменении
концентрации ПАВ на единицу. Количественной
мерой поверхностной активности является
величина g,
т.е. мерой поверхностной активности
является max
значение производной.
при Т,р=const
которая изменяется с изменением
концентрации. Физический смысл
производной: понижение поверхностного
натяжения раствора при изменении
концентрации ПАВ на единицу. Количественной
мерой поверхностной активности является
величина g,
т.е. мерой поверхностной активности
является max
значение производной.
![]() .
[g]=[Дж*м/моль]=[Н*м2/моль]
.
[g]=[Дж*м/моль]=[Н*м2/моль]
Из вышеперечисленного следует, что понятие поверхностной активности – относительно.
Поверхностную активность обычно измеряют графически. А именно: к изоторме поверхностного натяжения через ее начальную точку проводят касательную. Тангенс угла α выражается отношением катетов ОА и ОВ, взятых в единицах σ и с, численно равен величине поверхностной активности.
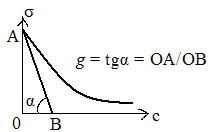
4. Изобразите седиментационные кривые для моно- и полидисперсной водных суспензий сульфата бария, полученные в случае, если экспериментатор находился в а)лаборатории, б)кабине космического корабля.
Наиболее распространенный и простой метод определения размеров частиц и функции распределения их по размерам является седиментационный анализ, основанный на различии скоростей оседания в поле силы тяжести частиц разного размера.
а) в лаборатории
![]() ,
где – r
– радиус частицы,
-
плотность ДФ, 0
– плотность
жидкости (ДС), g
– ускорение свободного падения,
- вязкость
жидкости, Uсед
– скорость движения частицы.
,
где – r
– радиус частицы,
-
плотность ДФ, 0
– плотность
жидкости (ДС), g
– ускорение свободного падения,
- вязкость
жидкости, Uсед
– скорость движения частицы.
![]() -
это уравнение описывает кинетику
седиментации монодисперсных систем.
Графически зависимость представлена
на рис.1,а). Точке B
соответствует
окончание процесса седиментации, и в
последующие моменты времени масса
осевших частиц не изменяется. Тангенс
угла наклона прямой характеризует
скорость оседания частиц дисперсной
фазы
-
это уравнение описывает кинетику
седиментации монодисперсных систем.
Графически зависимость представлена
на рис.1,а). Точке B
соответствует
окончание процесса седиментации, и в
последующие моменты времени масса
осевших частиц не изменяется. Тангенс
угла наклона прямой характеризует
скорость оседания частиц дисперсной
фазы
где – m – масса осевшего в-ва, mобщ – общая масса дисперсной фазы, H – первоначальная высота столба суспензии, - время осаждения, mобщ/Н - масса дисперсной фазы в объеме, приходящаяся на единицу высоты столба суспензии. →
![]() ,
при = r
и m = mобщ
,
,
при = r
и m = mобщ
,
![]() .
.
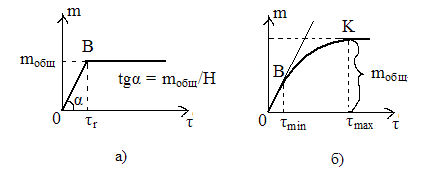
Рис.1 Седиментационные кривые получ в лаборатории для а) моно- , б)полидисперсных систем.
Для полидисперсной системы график – кривая плавная линия. По времени tmin рассчитывается rmax – радиус самых крупных частиц, по времени tmax рассчитывается rmin – радиус самых мелких частиц. Ордината этой касательной соответствует массе всех выпавших частиц (mобщ).
б) кабине космического корабля
? Сила тяжести в космосе = 0.
