2. Квазистационаpные явления в линейных пpоводниках

Eсли время запаздывания гараздо меньше длительных процессов, то процессы называются квазистационарными. Квазистационарные процессы можно исследовать с помощью постоянного тока, если применять эти законы к мгновенным значениям.

3. Переходный процесс: установление тока в цепи.

4. Переходный процесс: исчезновение тока в цепи.

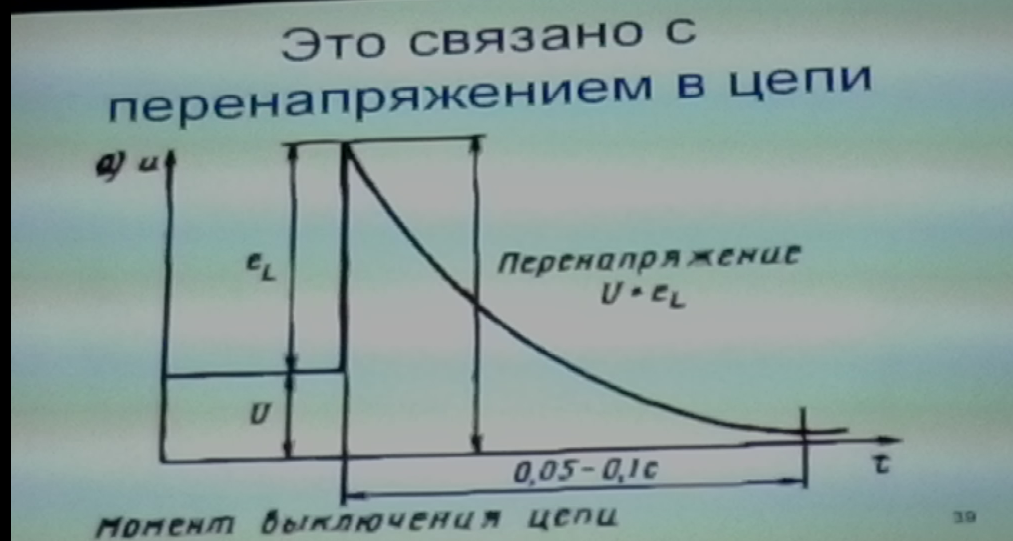
Лекция 14. ЭЛЕКТРОМАГНИТНЫЙ КОЛЕБАТЕЛЬНЫЙ КОНТУР

Свободные колебания в контуре без активного сопротивления.

Это периодические изменения электромагнитных величин, происходящих в идеальном колебательном контуре.

Идеальный колебательный контур – электрическая цепь, состоящая из конденсатора С и катушки индуктивности L.

Преобразование энергии в колебательном контуре: C*U²/2 = C*U²/2 + L*I²/2 = L*I²/2.

У равнение свободных электромагнитных колебаний:

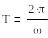
Напряжение на конденсаторе:

Метод векторных диаграмм.

Способ представления колебаний:

Построение векторных диаграмм. Каждое слагаемое колебание – стрелка. Амплитуда колебания – длина стрелки. Фаза колебания – угол между положительным направлением горизонтальной оси и стрелкой (против часовой стрелки – угол положительный).

Свободные затухающие колебания в контуре.

Реальный колебательный контур состоит из последовательно соединенных конденсаторов.

R/L=2*B, где B – коэффициент затухания.

1/L*C=w₀², - собственная циклическая частота контура.

Добротность колебательного контура Q:

- число колебаний, совершаемых за время затухания.

- время затухания. Время, за которое амплитуда уменьшится в е раз.

Критическое сопротивление:

Лекция 15 ПЕРЕМЕННЫЙ ТОК

15.1 Вынужденные электрические колебания

Вынужденными эл. колебаниями наз. незатухающие колебания в цепи под действием внешней периодически изменяющейся ЭДС.

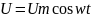
ДУ электрических колебаний

q-заряд

β-коэф. затухания

w0-собственная циклическая частота

w-циклическая частота переменной ЭДС

Um-амплитуда переменной ЭДС

L-индуктивность контура

Решение ДУ

R-активное сопротивление в цепи

wL-индуктивное сопротивление

- емкостное сопротивление

15.2 Цепи переменного тока. Импеданс

Виды цепей переменного тока:

1. Цепь с конденсатором емкостью С

2. Цепь с сопротивлением R

3. Цепь с катушкой индуктивности L

Импеданс:

-емкостное сопротивление

-индуктивное сопротивление

w-циклическая частота

L-индуктивность контура

С-емкость контура

15.3 Мощность в цепи переменного тока

При наличии только активного сопротивления

-мгновенное значение мощности

Средняя мощномть за период

или

При наличии реактивного сопротивления

-мгновенное значение мощности

-среднее значение

Лекция 16 Трансформаторы. Передача электрической энергии

Принцип работы ненагруженного трансформатора и его векторная диаграмма.

В режиме холостого хода первичная обмотка трансформатора включена в сеть на напряжение , а вторичная разомкнута . Для этого режима справедливы уравнения

Ток первичной обмотки представляет собой намагничивающий ток трансформатора. Построение векторной диаграммы (рис.10) начинают с вектора потока . ЭДС U1 и U2 отстают от потока на угол 90°. Реактивная составляющая тока намагничивания совпадает по фазе с потоком, а его активная составляющая опережает поток на 90°. Намагничивающий ток несколько опережает поток . Для получения вектора первичного напряжения необходимо построить вектор и прибавить к нему падения напряжений на активном и индуктивном сопротивлениях. Из векторной диаграммы видно, что очень мал. Обычно . Трансформатор потребляет из сети реактивную мощность на создание магнитного поля в трансформаторе.

Принцип работы нагруженного трансформатора и его векторная диаграмма

Векторные диаграммы при нагрузке строят по уравнениям (16). Вид векторной диаграммы зависит от характера нагрузки (рис. 14).

Векторная диаграмма а рис. 14 соответствует активно-индуктивной нагрузке, а векторная диаграмма б - активно-емкостной нагрузке.

Сопоставляя обе диаграммы, можно заключить, что при и увеличение активно-индуктивной нагрузки вызывает снижение напряжения , а при увеличении активно-емкостной нагрузки напряжение возрастает. Это объясняется тем, что при активно-индуктивной нагрузке происходит некоторое размагничивание трансформатора (поток Ф уменьшается, так как ток имеет составляющую, направленную навстречу току ), а при активно-емкостной нагрузке трансформатор дополнительно намагничивается (поток Ф возрастает, так как ток имеет составляющую, совпадающую с ).

Лекция 17 ЭЛЕКТРОМАГНИТНЫЕ ВОЛНЫ

1.Процесс распространения колебаний в пространстве называется волной.

От частицы к частице передается лишь состояние колебательного движения.

Hz и Ey – составляющие; Еm, Hm – амплитуды; - циклическая частота

– волновое число

Физический смысл

Амплитуда – величина максимального изменения составляющей

Циклическая частота с точностью до множителя равна числу колебаний в единицу времени

Волновое число равно числу длин волн, укладывающихся на отрезке метров.

Откуда берутся ЭМВ

1)Покоящийся заряд – постоянное электрическое поле.

2)Равномерно движ. заряд – переменное электрическое поле – переменное магнитное поле, но излучения нет.

2. Волновое уравнение

т. к. и , то

- для вакуума

3. Энеpгия и импульс электpомагнитной волны

Распространение электромагнитных волн связано с переносом энергии.

Объемная плотность энергии W, электромагнитной волны.

Поток энергии через еденичную площадку, перпендикулярную направлению распространения волны в еденицу времени

Поток энергии через площадку dS:

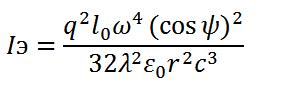
Излучение диполя.

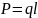
Интенсивность излучения диаполя

Лекция 6

Энергия электростатического поля

Энергия взаимодействия системы электрических зарядов:

Рассмотрим два заряда: q₁ и q₂

Потенциальная энергия их взаимодействия

W₁₂= 1 / 4 _{0 *} q₁q₂/r₁₂ W₁₂= 1 / 4 _{0 *} q₁/r₁₂*q₂= ₁₂*q₂

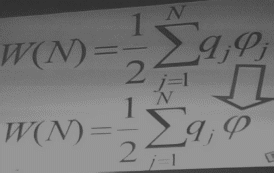
W₂₁= 1 / 4 _{0 *} q₁q₂/r₂₁ W₂₁= 1 / 4 _{0 *} q₁/r₂₁*q₁= ₂₁*q₁

Где ₂₁- потенциал, создаваемый зарядом q₁ в той точке, в которой находится заряд q₂

А ₁₂- потенциал, создаваемый зарядом q₁ в той точке, в которой находится заряд q₁

Но W₂₁=W₁₂ т.к. r₁₂=r₂₁

Значит : W(2)=W₁₂+W₂₁/2 W(2)= ₁₂*q₂+ ₂₁*q₁/2

Энергия заряженного проводника

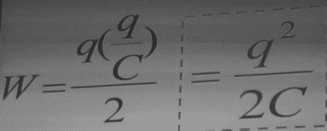
Для всех точек проводника потенциал одинаков

=const=

W=q* /2

Энергия конденсатора

Рассмотрим две параллельные одинаково незаряженные пластины

Перенесём заряд +dq с одной пластины на другую

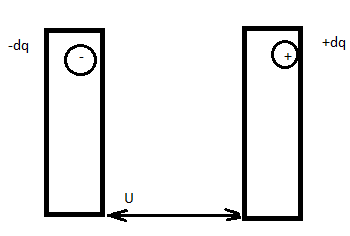U=-

Элементарная работа внешних сил по переносу следующей порции заряда равна:

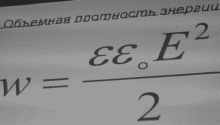
dA = U dq

Работа внешних сил при увеличении заряда конденсатора от 0 до q

C= dq/dU => dq = CdU

Энергия заряженного конденсатора равна : С = q/U

Объёмная плотность энергии электростатического поля

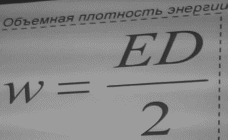
W= CU²/2 =

Объёмная плотность энергии

Индукция электростатического поля : D= ₀E