11. Векторное произведение и его свойства, вычисление через координаты

Векторным произведением вектора на вектор называется вектор (обозначим его ), удовлетворяющий следующим условиям.

1. , где .

2. и .

3. Направление вектора выбрано так, что со стороны вектора поворот от к происходит против часовой стрелки.

Свойства векторного произведения.

1.

2. , - вещественное число

3.

Пример

Найти площадь параллелограмма и угол между его диагоналями, если длина сторон параллелограмма и угол между ними .

Решение.

Пусть и - векторы, построенные на сторонах параллелограмма. Площадь параллелограмма . Заметим, что . Диагонали параллелограмма – это векторы и .

Пусть - угол между диагоналями. Тогда

Ответ: ; .

Векторное произведение векторов.

 

Определение: Векторным произведением упорядоченной пары векторов a и b называется вектор [a,b], такой что

1. | [a,b] |=S_a,b, где S_a,b – площадь параллелограмма, построенного на векторах a и b. (Если a || b, то S_a,b=0.)

2. a [a,b] b.

3. a, b, [a,b] – правая тройка.

Свойства векторного произведения:

1. [a,b] = -[b,a]

2. [a,b] = θ ó a || b

3. [a₁+a₂,b] = [a₁,b]+[a₂,b]

4. λ·[a,b] = [λ·a,b] = [a,λ·b] 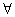λ R.

Утверждение 2: В декартовой системе координат (базис i, j, k), a={x₁, y₁, z₁}, b={x₂, y₂, z₂}

=> [a,b] =

=

12. Смешанное произведение векторов.

 

Определение : Смешанным произведением упорядоченной тройки векторов a, b и c называется число <a, b, c>, т.ч. <a,b,c>=([a,b],c).

 

Утверждение : <a,b,c>=V_a,b,c, если a,b,c – правая тройка, или <a,b,c>= -V_a,b,c, если a,b,c – левая тройка. Здесь V_a,b,c – объём параллелепипеда, построенного на векторах a, b и c. (Если a, b и c компланарны, то V_a,b,c=0.)

 

Утверждение : В декартовой системе координат, если a={x₁, y₁, z₁}, b={x₂, y₂, z₂},

с={x₃, y₃, z₃}, => <a,b,c>= .

13. Прямая на плоскости. Виды уравнений прямой.

Понятие "уравнение линии" - есть основное понятие аналитической геометрии. Из него вытекают две основные задачи аналитической геометрии на плоскости:

А) Дана линия, рассматриваемая как множество точек. Составить алгебраическое уравнение этой линии.

Б) Дано уравнение некоторой линии. Изучить по этому уравнению её геометрические свойства: форму и расположение.

Линия называется линией n-го порядка (n=1, 2, 3, …), если она определяется уравнением n-ой степени относительно текущих прямоугольных координат.

Ax+By+C=0 - кривые первого порядка;

Ax²+2Bxy+Cy²+2Dx+2Ey+F=0 - кривые второго порядка

.Кривая первого порядка - есть прямая линия.

Уравнение с угловым коэффициентом.

k= tg α – угловой коэффициент.

Если b=0 то прямая проходит через начало координат. Уравнение примет вид

Если α=0, то k = tg α = 0. То прямая пройдет параллельно оси ох.

Если α=π/2, то уравнение теряет смысл. В этом случае уравнение примет

вид и пройдет

параллельно оси оу.

Общее уравнение прямой.

A, B, C – произвольные числа, причем А и В не равны нулю одновременно.

· Если В=0, то уравнение имеет вид

или . Это уравнение

прямой, параллельной оси оу. и проходящей через точку

· Если В≠0, то получаем уравнение с угловым коэффициентом .

· Если А=0, то уравнение имеет вид . Это уравнение прямой, параллельной оси ох.

· Если С=0, то уравнение проходит через т. О (0;0).

Уравнение прямой, проходящей через точку, в данном направлении.

т М (х₀;у₀).

Уравнение прямой записывается в виде .

Подставим в это уравнение точку М

Решим систему:

Уравнение прямой, проходящей через 2 точки.

К (х₁;у₁) М (х₂;у₂)

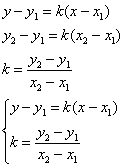
Уравнение прямой в отрезках.

К (а;0); М (0;b)

Подставим точки в уравнение прямой:

Уравнение прямой, проходящей через данную точку, перпендикулярно данному

вектору.

М₀ (х₀;у₀).

Возьмем произвольную точку М (х;у).

Т.к. , то

Нормальное уравнение прямой.

Уравнение прямой можно записать в виде:

Т.к. ; , то:

Угол между прямыми.

Дано: прямые L₁ и L₂ с угловыми коэффициентами

Требуется найти угол между прямыми: