5. Матричная форма записи системы линейных алгебраических уравнений. Виды слау:

Система уравнений вида.

(1)

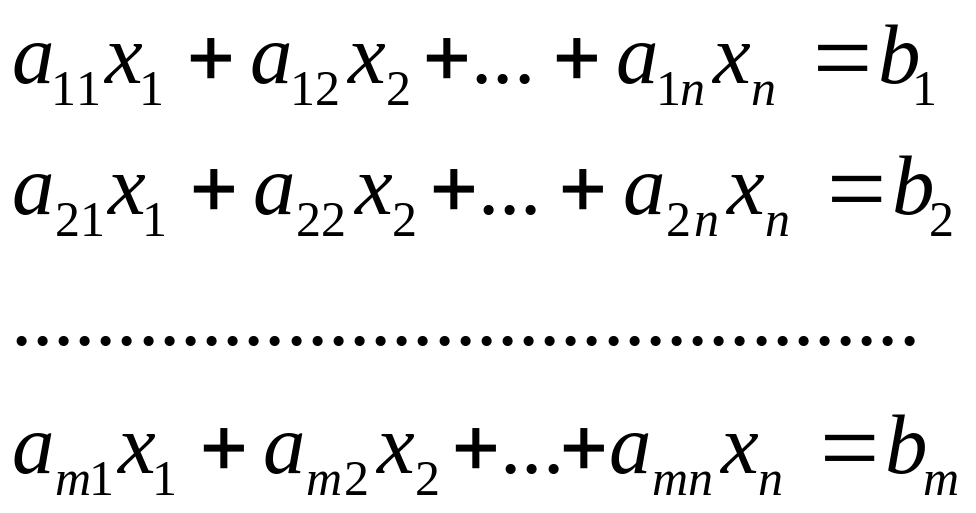
Называется системой m линейных уравнений с n неизвестными .

коэффициенты при неизвестных, свободные члены.

Если все свободные члены равны нулю, то система называется однородной.

Решением системы линейных уравнений (1) называется такая система n чисел , что каждое из уравнений системы (1) превращается в тождество после замены в нем неизвестных соответствующими числами .

Совокупность всех решений называется множеством решений.

Две системы линейных уравнений называются эквивалентными, если они имеют одинаковые множества решений.

Если система линейных уравнений не имеет ни одного решения, то она называется несовместной, например

Cовместная система называется определенной, если она имеет единственное решение:

Совместная система называется неопределенной, если решений больше, чем одно: где

Теория системы линейных уравнений может быть наглядно описана с помощью матриц. Коэффициенты при неизвестных в системе (1) записывают в виде матрицы размера (m n) :

А = которая называется матрицей системы (1).

Свободные члены образуют столбец размера

В = который называется столбцом свободных членов.

Неизвестные записываются тоже в виде столбца размера

X = .

Тогда систему (1) можно записать в виде

(2) АХ = В

Такая запись называется матричной записью системы.

Убедимся, что это действительно так:

АХ = =

Мы получили левую часть системы (1).

Далее, из равенства матриц АХ и В следует, что соответствующие их элементы равны, и мы получаем следующую систему равенств:

6. Решение слау по методу Крамера и с помощью обратной матрицы

Формулы Крамера.

В определенных системах каждое из неизвестных может быть вычислено по следующей формуле:

(4)

где D=detA - определитель системы, а _, представляет собой определитель, полученный из определителя системы D заменой i-го столбца столбцом свободных членов.

Пример Решим систему по формулам Крамера.

Определитель системы D был вычислен в предыдущем примере:

Определитель получится из определителя D, если в последнем первый столбец заменить столбцом свободных членов В:

Таким образом, .

Определитель D₂ получится из определителя D, если в последнем второй столбец заменить столбцом свободных членов:

Cледовательно,

Аналогично D₃ получается из D заменой третьего столбцом свободных членов:

Матричный способ решения определенных систем.

Как говорилось ранее, система линейных алгебраических уравнений может быть записана в матричной форме

где А-матрица системы, Х-столбец неизвестных, В-столбец свободных членов.

Т.к. у определенных систем detA 0, то у матрицы системы существует обратная матрица . Домножим обе части равенства слева на

Произведение обратной матрицы на саму матрицу по определению есть единичная матрица: следовательно, имеет следующее равенство:

Т.к. единичная матрица имеет порядок n, а столбец неизвестных размер матрицы Е и Х, являются сцепленными в таком порядке, следовательно, существует их произведение, которое представляет собой столбец неизвестных Х. И мы имеем явную формулу для вычисления столбца неизвестных в определенных системах:

(3)

Т.к. det A 0, следовательно, существует обратная матрица которую найдем по формуле: