1. Матрицы: определение,
виды матриц,
линейные операции с
матрицами.
Матрицей
размера m
n называется
таблица состоящая из
m
n
выражений, которые расставлены в m
строк и n
столбцов:
Выражения
называются элементами
матрицы.
Положение элемента в таблице характеризуется двойным индексом; первый индекс i означает номер строки, второй индекс j-номер столбца, на пересечении которых стоит элемент
(m
n)-матрица,
все элементы которой равны нулю,
называется нулевой
(m
n
) - матрицей.
Матрица размера
1
n,
состоящая из одной строки, называется
матрицей
-
строкой:
Матрица размера
m
1, состоящая из одного столбца, называется
матрицей
- столбцом:
.
Каждая матрица, которая получается из ( m n )- матрицы А вычеркиванием каких-либо строк и столбцов, называется подматрицей матрицы A.
Если в матрице А взаимно переставить местами строки и столбцы, то полученная матрица называется транспонированной к А и обозначается АТ; она будет иметь размер n m :
=
.
Матрица, у которой число строк равно числу столбцов ( т.е. матрица размера n n ), называется квадратной матрицей порядка n.
Элементы квадратной
матрицы
образуют
главную
диагональ
матрицы (они стоят в таблице на диагонали
квадрата, проходящей из левого верхнего
угла в нижний правый); элементы
образуют побочную
диагональ.
Квадратная матрица, у которой все
элементы главной диагонали равны
единице, а остальные равны нулю,
называется единичной
и обозначается
Е:
Е =
.
Действия над матрицами.
1) Равенство матрицы
Две матрицы
и
называются равными, если они имеют
одинаковый размер и их соответствующие
элементы ( элементы, стоящие на одних
и тех же местах) равны между собой, т.е.
если
и
при всех i и j; тогда пишут А=В.
2) Сложение матриц одинакового размера.
Сумма двух матриц
А + В
одинакового размера есть матрица С
того же
размера с элементами
при всех i
и j,
т.е. сложение матриц одинакового размера
происходит поэлементно.
3) Умножение матриц на действительное число.
Произведение
матрицы
на действительное число
есть матрица
т.е.
умножение матрицы на действительное
число происходит поэлементно.
Свойства сложения и умножения на число.
1. А + В = В + А
2. ( А + В ) + С = А + ( В + С )
3. А + Х = В
Х = В - А - разность матриц В и А
4. А + О = О + А = А
5. (
)
А =
(
А )
6. ( + ) А = А + А
7. ( А + В ) = А + В
2.Умножение матриц
Матрицы
и
называют
сцепленными в такой последовательности,
если n=r
, т.е. если число столбцов первой матрицы
равно числу строк второй.
Матрицы А и В могут быть сцепленными, в то время, как матрицы В и А таковыми могут не является. Например, если матрица А размера 2 * 3, а матрица В размера 3 *4 , то матрицы А и В являются сцепленными, в то же время матрицы В и А не являются сцепленными.
Произведение АВ двух сцепленных в такой последовательности матриц есть
матрица
,
размера ( m * s) , где
т.е. элемент,
стоящий
в i- ой строке и j- ом столбце матрицы произведения, получается в виде суммы
произведений
элементов, стоящих на одинаковых местах
в i-ой
строке матрицы А
и j-ом
столбце матрицы В.
Таким образом, чтобы получить
,
мы должны первый элемент i-ой
строки матрицы A
умножить
на первый элемент j-го
столбца матрицы В,
затем второй элемент i-ой
строки матрицы А
умножить на второй элемент j-го
столбца матрицы
В, и т.д., а
затем все эти произведения сложить
между собой.
В данном примере
произведение ВА
не определено,
т.к. матрицы В
и А
не являются сцепленными. Если даже
существуют оба произведения АВ
и ВА,
то могут отличаться друг от друга, т.е.
в общем случае АВ
ВА.
Если АВ=ВА, то матрицы А и В называются перестановочными. Существует делитель нуля, т.е. существуют такие ненулевые матрицы, произведение которых есть нулевая матрица, например:
=
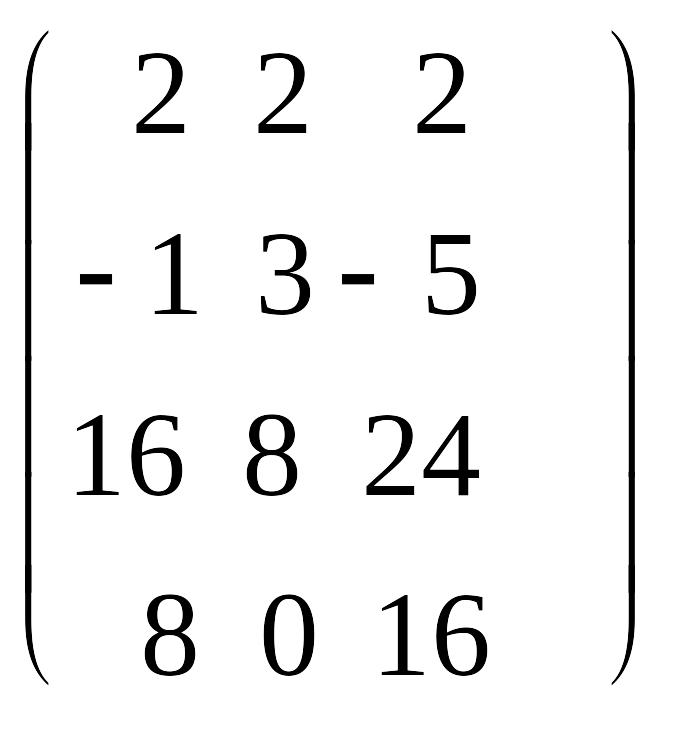Следовательно, из того, что АВ=АС, А 0 в общем случае не следует, что В=С.
Если
,то
домножение ее на единичную матрицу, не
изменит самой матрицы :
На множестве квадратных матриц одного порядка всегда выполнимы действия сложения и умножения.