Молекулярно-кинетическая теория идеальных газов

●Закон Бойля-Мариотта

при ,

где p – давление; V – объем; Т – термодинамическая температура; m – масса газа.

● Закон Гей-Люссака и закон Шарля

, или при ;

, или при ,

где t – температура по шкале Цельсия; и - соответственно объем и давление при 0⁰ С; коэффициент ; индексы 1 и 2 относятся к произвольным состояниям.

● Закон Дальтона для давления смеси n идеальных газов

,

где - парциальное давление i – го компонента смеси.

● Уравнение состояния идеального газа (уравнение Менделеева-Клапейрона)

,

где – газовая постоянная, μ – молярная масса газа.

● Зависимость давления газа от концентрации n молекул и температуры Т

,

где – постоянная Больцмана ( k=R/N_a , – постоянная Авогадро).

● Основное уравнение молекулярно-кинетической теории идеальных газов

,

или

,

или

,

где - средняя квадратичная скорость молекул; Е- суммарная кинетическая энергия поступательного движения всех молекул газа; n- концентрация молекул; - масса одной молекулы; - масса газа; N- число молекул в объеме газа V.

● Скорость молекул:

наиболее вероятная

;

средняя квадратичная

;

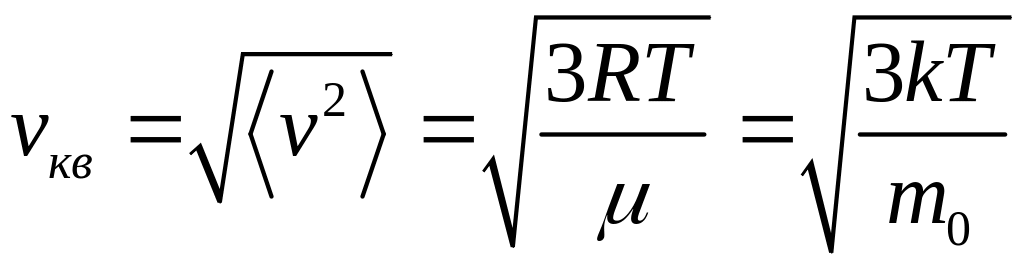средняя арифметическая

.

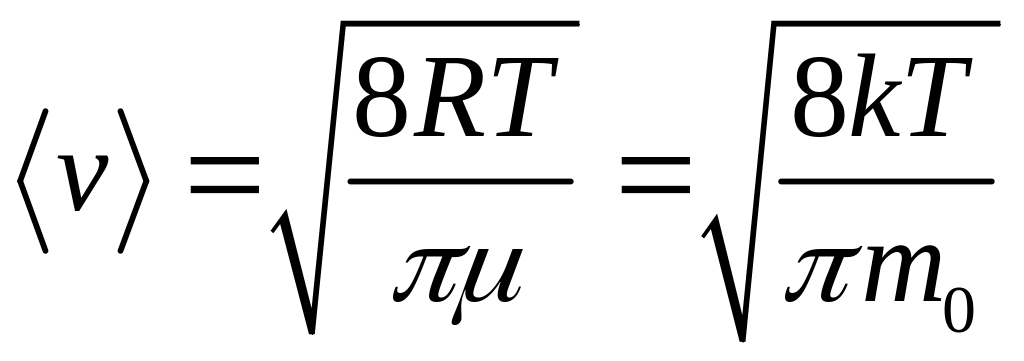● Средняя кинетическая энергия поступательного движения молекулы идеального газа

.

● Закон Максвелла для распределения молекул идеального газа по скоростям

,

где функция ( ) распределения молекул по скоростям определяет относительное число молекул из общего числа N молекул, скорости которых лежат в интервале от до .

● Закон Максвелла для распределения молекул идеального газа по энергиям теплового движения

,

где функция f(ε) распределения молекул по энергиям теплового движения определяет относительное число молекул из общего числа N молекул, которые имеют кинетические энергии , заключенные в интервале от ε до ε+dε.

● Барометрическая формула

,

где и – давление газа на высоте h и h₀.

● Распределение Больцмана во внешнем потенциальном поле

,

где n и n₀ – концентрация молекул на высоте h и h₀ .

● Среднее число соударений, испытываемых молекулой газа за 1 секунду,

,

где d –эффективный диаметр молекулы; n – концентрация молекул; - средняя арифметическая скорость молекул.

● Средняя длина свободного пробега молекул газа

.

● закон теплопроводности Фурье

,

где Q теплота, прошедшая посредством теплопроводности через площадь S за время t; - градиент температуры; λ- теплопроводность:

,

где с_v – удельная теплоемкость газа при постоянном объеме; ρ- плотность газа.

● Закон диффузии Фика

,

где М – масса вещества, переносимая посредством диффузии через площадь S за время t; - градиент плотности, D – диффузия:

.

● Закон Ньютона для внутреннего трения (вязкости)

,

где F – сила внутреннего трения между движущимися слоями площадью S;

- градиент скорости; η – динамическая вязкость:

.

Основы термодинамики

● Средняя кинетическая энергия поступательного движения, приходящаяся на одну степень свободы молекулы,

.

● Средняя энергия молекулы

,

где - число степеней свободы.

● Внутренняя энергия газа

,

где – количества вещества; m – масса газа; μ – молярная масса газа.

● Первое начало термодинамики

,

где Q – количество теплоты, сообщенное системе или отданное ею; - изменение её внутренней энергии; А – работа системы против внешних сил.

● Первое начало термодинамики для малого изменения системы

.

● Молярные теплоемкости газа при постоянном объеме и постоянном давлении

, .

● Уравнение Р. Майера, для 1 моля идеального газа

.

● Изменение внутренней энергии идеального газа

.

● Работа, совершаемая газом при изменении его объема,

.

● Полная работа при изменении объема газа

,

где V₁ и V₂ – соответственно начальный и конечный объемы газа.

● Работа газа:

при изобарном процессе

, или ;

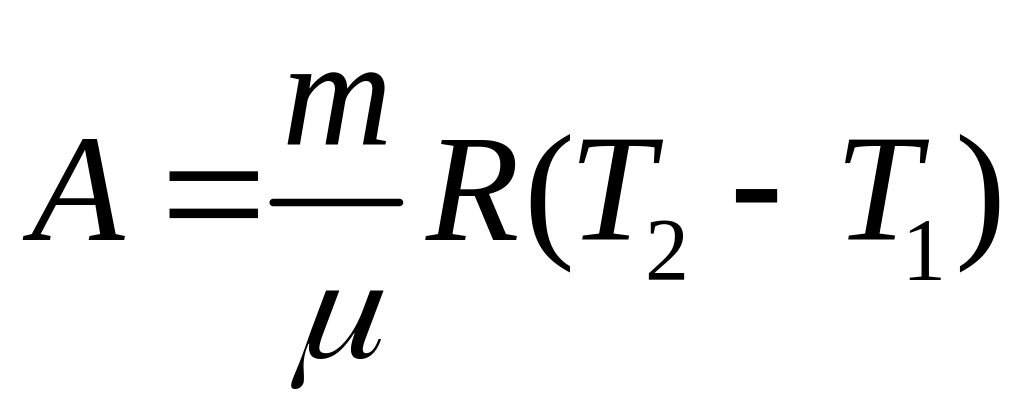при изотермическом процессе

, или .

● Уравнение адиабатического процесса (уравнение Пуассона)

где - показатель адиабаты.

● Работа в случае адиабатического процесса

или ,

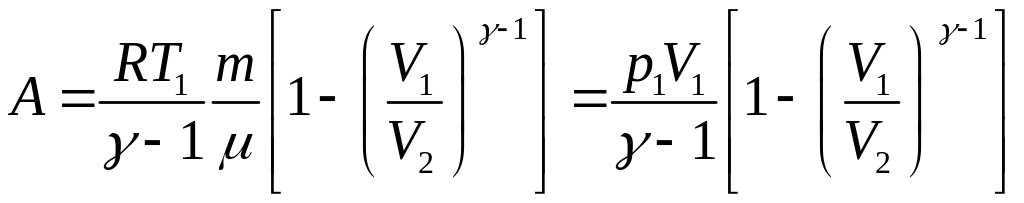где T₁ , T₂ и V_1, V₂ – соответственно начальные и конечные температура и объем газа.

● Термический коэффициент полезного действия для кругового процесса (цикла)

,

где Q₁ – количество теплоты, полученное системой; Q₂ – количество теплоты, отданное системой; А – работа, совершаемая за цикл.

● Термический коэффициент полезного действия цикла Карно

,

где T₁ – температура нагревателя; T₂ – температура холодильника.

● Изменение энтропии при равновесном переходе из состояния 1 в состояние 2, в переменных Р V

.