5. Закон Джоуля - Ленца
Проводник
нагревается, если по нему протекает
электрический ток. Джоуль и Ленц
установили, что количество выделившегося
тепла Q
= I
Rt,
(28)
где I - ток, R - сопротивление, t - время протекания тока. Легко доказать, что
Q = I Rt = UIt = U 2 t/R = qU, (29)
где q = It - электрический заряд.
Если ток изменяется со временем (т. е. в случае непостоянного тока), то
Q
=
=
,
(30)
где i - мгновенное значение тока.
Нагревание проводника происходит за счет работы, совершаемой силами электрического поля над носителями заряда. Эта работа
A = qU = UIt =I Rt = U t / R . (31)
Работа А, энергия W , количество тепла Q в СИ измеряются в Дж.
Так
как мощность характеризует работу,
совершаемую в единицу времени, т.е. Р
=
,
то
P = UI = I R = U / R . (32)
Мощность в СИ измеряется в ваттах: 1 Вт = 1 Дж / 1 с; откуда 1 Дж = 1 Втс;
3600
Дж = 1Вт час,
3,6 •10
Дж
= 1
кВт час.
Формулы (31) и (32) позволяют рассчитать полезную работу и полезную мощность. Затраченная работа и мощность определяется по формулам
A
= q
=
It
= I
(R
+ r)t
=
t.
(33)
P
=
=
I
= I
(R
+ r)
=
.
(34)
Отношение полезной работы (мощности) к затраченной характеризует КПД источника
=
=
=
.
(35)
Из
(35)
следует, что при R0,0;
R,1.Но
при
R
ток
I
0
и поэтому
А О и Р 0.
Определим
величину
R
,
при котором выделится максимальная
мощность. Легко показать, что это
наступает при R
= r,
тогда PMAКС=I
R
=
=
,
(36)
КПД в этом случае будет 50%.
6. Закон Джоуля - Ленца в дифференциальной форме
Согласно закону Джоуля - Ленца (28) в элементарном цилиндрическом объеме dV с площадью поперечного сечения dS и длиной dl за время dt выделится тепло
dQ
=I
Rdt
=(jdS)
=
j
dldSdt
=
j
dVdt.
Разделив
на dV
и dt,
найдем количество тепла, выделяющееся
в единицу времени в единице объема
Q
=
=
j
. (37)
здесь Q -называется удельной тепловой мощностью тока, которая в СИ измеряется в Вт/м3.
С
учетом
(16)
из
(37)
следует, что Q
=
j
=
.
(38)
Формулы (37) и (38) выражают закон Джоуля - Ленца в дифференциальной форме.
13)Сторонние силы. ЭДС. Источники ЭДС. Напряжение. Закон Ома для замкнутой цепи и участка цепи, содержащего источник ЭДС.
Сторонние силы. Источники ЭДС.
Для существования постоянного тока необходимо наличие в электрической цепи устройства, способного создавать и поддерживать разности потенциалов на участках цепи за счет работы сил неэлектростатического происхождения. Такие устройства называются источниками постоянного тока. Силы неэлектростатического происхождения, действующие на свободные носители заряда со стороны источников тока, называются сторонними силами.
Природа сторонних сил может быть различной. В гальванических элементах или аккумуляторах они возникают в результате электрохимических процессов, в генераторах постоянного тока сторонние силы возникают при движении проводников в магнитном поле. Источник тока в электрической цепи играет ту же роль, что и насос, который необходим для перекачивания жидкости в замкнутой гидравлической системе. Под действием сторонних сил электрические заряды движутся внутри источника тока против сил электростатического поля, благодаря чему в замкнутой цепи может поддерживаться постоянный электрический ток.
При перемещении электрических зарядов по цепи постоянного тока сторонние силы, действующие внутри источников тока, совершают работу.
Физическая величина, равная отношению работы Aст сторонних сил при перемещении заряда q от отрицательного полюса источника тока к положительному к величине этого заряда, называется электродвижущей силой источника (ЭДС):
|
Таким образом, ЭДС определяется работой, совершаемой сторонними силами при перемещении единичного положительного заряда. Электродвижущая сила, как и разность потенциалов, измеряется в вольтах (В).
Цепь постоянного тока можно разбить на отдельные участки. Те участки, на которых не действуют сторонние силы (т. е. участки, не содержащие источников тока), называются однородными. Участки, включающие источники тока, называются неоднородными.
При
перемещении единичного положительного
заряда по некоторому участку цепи работу
совершают как электростатические
(кулоновские), так и сторонние силы.
Работа электростатических сил равна
разности потенциалов Δφ12 = φ1 – φ2
между начальной (1) и конечной (2) точками
неоднородного участка. Работа сторонних
сил равна по определению электродвижущей
силе
12,
действующей на данном участке. Поэтому
полная работа равна
|
Величину U12 принято называть напряжением на участке цепи 1–2. В случае однородного участка напряжение равно разности потенциалов:
|
Закон Ома для замкнутой цепи и участка цепи, содержащего источник ЭДС.
Немецкий физик Г. Ом в 1826 году экспериментально установил, что сила тока I, текущего по однородному металлическому проводнику (т. е. проводнику, в котором не действуют сторонние силы), пропорциональна напряжению U на концах проводника:
|
где R = const.
Величину R принято называть электрическим сопротивлением. Проводник, обладающий электрическим сопротивлением, называется резистором. Данное соотношение выражает закон Ома для однородного участка цепи: сила тока в проводнике прямо пропорциональна приложенному напряжению и обратно пропорциональна сопротивлению проводника.
Для участка цепи, содержащего ЭДС, закон Ома записывается в следующей форме:
|
Это соотношение принято называть обобщенным законом Ома или законом Ома для неоднородного участка цепи.
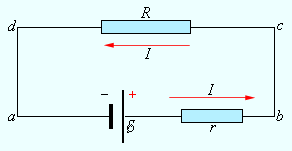
На рис. изображена замкнутая цепь постоянного тока. Участок цепи (cd) является однородным.
|
|
|
|
По закону Ома IR = Δφcd. |
|
Участок (ab) содержит источник тока с ЭДС, равной .
По закону Ома для неоднородного участка,
Ir = Δφab + . |
Сложив оба равенства, получим:
I (R + r) = Δφcd + Δφab + . |
Но
Δφcd = Δφba = – Δφab.
Поэтому
|
Эта формула выражет закон Ома для полной цепи: сила тока в полной цепи равна электродвижущей силе источника, деленной на сумму сопротивлений однородного и неоднородного участков цепи.
Сопротивление r неоднородного участка на рис. 1.8.2 можно рассматривать как внутреннее сопротивление источника тока. В этом случае участок (ab) на рис. 1.8.2 является внутренним участком источника.
14)Правила Кирхгофа. Микроскопическая природа сопротивления.
Правила Кирхгофа.