ФИЗИКА ЭКЗАМЕН

1) Макроскопическая система. Микро- и макроскопические параметры системы: статистический и термодинамический подходы к описанию свойств системы.

Микроскопические параметры – это параметры малых частиц (масса молекулы, ее скорость, импульс, энергия), характеризующие движение отдельной частицы.

Макроскопические параметры – это параметры, характеризующие свойства газа как целого (масса газа, давление, объем, температура)

Термодинамический подход. Систему рассматривают без учета её внутренней структуры. При этом используют понятия и величины, относящиеся к системе в целом. Например, идеальный газ в состоянии равновесия характеризуют объёмом, давлением и температурой (V, P и T). Экспериментально устанавливают связь между этими величинами. Для термодинамического подхода характерно использование термодинамических потенциалов для описания систем, находящихся в равновесном или слабо неравновесном состоянии. Для сильно неравновесных нелинейных систем описание состояния через потенциалы невозможно.

Статистический подход. Динамическое описание системы, содержащей большое число частиц, невозможно. Для изучения макросистем применяют статистические методы, использующие понятия и величины, относящиеся не к отдельным частицам, а к большим совокупностям частиц. Законы поведения совокупностей большого числа частиц, использующие статистические методы, называются статистическими закономерностями. Эти закономерности, как и величины, описывающие состояние системы, зависят от того, в каком состоянии находится система: равновесном или неравновесном.

2)Идеальный газ. Уравнение состояния. Основное уравнение кинетической теории газов. Молекулярно-кинетический смысл давления и температуры.

Идеальный газ — математическая модель газа, в которой предполагается, что потенциальной энергией взаимодействия молекул можно пренебречь по сравнению с их кинетической энергией. Между молекулами не действуют силы притяжения или отталкивания, соударения частиц между собой и со стенками сосуда абсолютно упруги, а время взаимодействия между молекулами пренебрежимо мало по сравнению со средним временем между столкновениями.

Основное уравнение состояния идеального газа

Основное уравнение молекулярно кинетической теории идеального газа

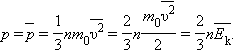
Молекулярно-кинетический смысл давления и температуры

Температура – это средняя кинетическая энергия движения молекул.

Давление - сила, действующая на единицу площади поверхности (соударение молекул со стенками сосуда).

3)Барометрическая формула: распределение Больцмана. Распределение Максвелла молекул по скоростям: средние скорости молекул.

Барометрическая формула

Для идеального газа, имеющего постоянную температуру T и находящегося в однородном поле тяжести (во всех точках его объёма ускорение свободного падения g одинаково), барометрическая формула имеет следующий вид:

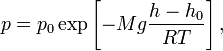
где p — давление газа в слое, расположенном на высоте h, p₀ — давление на нулевом уровне (h = h₀), M — молярная масса газа, R — газовая постоянная, T — абсолютная температура. Из барометрической формулы следует, что концентрация молекул n (или плотность газа) убывает с высотой по тому же закону:

Барометрическая формула позволяет вычислить атмосферное давление в зависимости от высоты или, измеряя давление, найти высоту    где р — давление на высоте h. 

Распределение Максвелла молекул по скоростям.

Распределение Максвелла, распределение по скоростям частиц (молекул) макроскопической физической системы, находящейся в состоянии термодинамического равновесия, (в отсутствии внешнего поля, при условии, что движение частиц подчиняется законам классической механики. Установлено Дж. К. Максвеллом в 1859.

Закон Максвелла о распределении молекул идеального газа по скоростям основан на предположениях, что газ состоит из большого числа N одинаковых молекул, его температура постоянна, а молекулы совершают тепловое хаотическое движение. При этом на газ не действуют силовые поля.

Средняя скорость

Подставляя   и интегрируя, мы получим

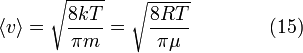
4) Первое начало термодинамики. Внутренняя энергия, её распределение по степеням свободы. Квазиравновесные процессы; теплоемкости идеального газа. Адиабатический процесс. Уравнение Пуассона. Первое начало термодинамики

Количество теплоты, полученное системой, идёт на изменение её внутренней энергии и совершение работы против внешних сил

Внутренняя энергия, её распределение по степеням свободы

Закон Больцмана о равномерном распределении энергии по степеням свободы молекул - для статистической системы, которая находится в состоянии термодинамического равновесия, на каждую поступательную и вращательную степени свободы приходится в среднем кинетическая энергия, равная kT/2, а на каждую колебательную степень свободы — в среднем энергия, равная kT. Колебательная степень обладает вдвое большей энергией, т.к. на нее приходится как кинетическая энергия (как в случае поступательного и вращательного движений), так и потенциальная, причем средние значения потенциальной и кинетической и энергии одинаковы. Значит, средняя энергия молекулы    где i — сумма числа поступательных, числа вращательных в удвоенного числа колебательных степеней свободы молекулы: i=i_пост+i_вращ+2i_колеб 

Квазиравновесные процессы, теплоёмкости идеального газа

Квазиравновесный процесс - характеризуется бесконечно медленным переходом системы из одного состояния в другое, вследствие ничтожно малого различия противодействующих внешних воздействий на систему и внутренних сил противодействия.

Квазистатические процессы всегда обратимы. Это следует из того, что любое промежуточное состояние есть состояние термодинамического равновесия, а оно не зависит от того, идет процесс в прямом или обратном направлении.

Адиабатический процесс

Термодинамический процесс в макроскопической системе, при котором система не получает и не отдаёт тепловой энергии.

Квазистатические адиабатические процессы.

Уравнение Пуассона

Адиаба́та Пуассо́на — линия на термодинамической диаграмме состояний, изображающая обратимый адиабатический процесс для идеального газа, описывается уравнением Пуассона:

5) Циклы. Тепловые машины, их КПД. Второе начало термрдинамики. Цикл Карно. Энтропия. Принцип возрастания энтропии. Статистический смысл энтропии и второго начала термодинамики. Третье начало термодинамики.

Циклы

Термодинами́ческие ци́клы — круговые процессы в термодинамике, то есть такие процессы, в которых начальные и конечные параметры, определяющие состояние рабочего тела (давление, объём, температура, энтропия), совпадают.

Тепловые машины

Тепловая машина состоит из нагревателя, рабочего тела и охладителя рабочего тела. Охладителем, в конечном счете, служит окружающая среда. Тепловая машина работает по принципу замкнутого цикла, совершая круговой процесс.

КПД

Отношение полезной работы, совершенной машиной, к количеству полученного тепла составляет КПД тепловой машины

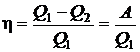
Второе начало термодинамики

Второе начало термодинамики — физический принцип, накладывающий ограничение на направление процессов передачи тепла между телами.

Второе начало термодинамики гласит, что невозможен самопроизвольный переход тепла от тела, менее нагретого, к телу, более нагретому.

Второе начало термодинамики запрещает так называемые вечные двигатели второго рода, показывая что коэффициент полезного действия не может равняться единице, поскольку для кругового процесса температура холодильника не должна равняться 0

Цикл Карно

Цикл Карно́ — идеальный термодинамический цикл. Тепловая машина Карно, работающая по этому циклу, обладает максимальным КПД из всех машин, у которых максимальная и минимальная температуры осуществляемого цикла совпадают соответственно с максимальной и минимальной температурами цикла Карно. Состоит из 2 адиабатическихи 2 изотермических процессов.

Одним из важных свойств цикла Карно является его обратимость: он может быть проведён как в прямом, так и в обратном направлении, при этом энтропия адиабатически изолированной (без теплообмена с окружающей средой) системы не меняется.

Энтропия

Энтропия, функция состояния S термодинамической системы, изменение которой dS для бесконечно малого обратимого изменения состояния системы равно отношению количества теплоты   полученного системой в этом процессе (или отнятого от системы), к абсолютной температуре Т:

Принцип возрастания энтропии

В адиабатически изолированной термодинамической системе энтропия не может убывать: она или сохраняется, если в системе происходят только обратимые процессы, или возрастает, если в системе протекает хотя бы один необратимый процесс.

     Записанное утверждение является ещё одной формулировкой второго начала термодинамики.

Статистический смысл энтропии и второе начало термодинамики

Л.Больцман принял одинаковую вероятность реализации любого микросостояния, возможного для заданного макросостояния, и определил термодинамическую вероятность   макросостояния на основе формулы

 .                                                   (10.1)

Здесь термодинамическая вероятность может принимать значения много больше 1.

Используя термодинамическую вероятность (10.1), Л.Больцман дал статистическое (вероятностное) определение энтропии S макросостояния с помощью выражения

 ,                                        (10.2)

где k – постоянная Больцмана. Натуральный логарифм в (10.2) обеспечивает аддитивность энтропий подсистем полной системы, поскольку статистический вес полной системы равен произведению статистических весов ее макроскопических подсистем.

В соответствии со вторым началом термодинамики энтропия равновесного состояния замкнутой системы принимает максимальное значение. Следовательно, статистический вес и термодинамическая вероятность равновесного состояния также максимальные. Условие максимума статистического веса макросостояния позволяет найти наиболее вероятные распределения частиц по ячейкам фазового пространства и, соответственно, по энергиям как в классической, так и в квантовой физике.

Другая формулировка второго начала термодинамики основывается на понятии энтропии:

«Энтропия изолированной системы не может уменьшаться» (закон неубывания энтропии).

Третье начало термодинамики

Приращение энтропии при абсолютном нуле температуры стремится к конечному пределу, не зависящему от того, в каком равновесном состоянии находится система

где x — любой термодинамический параметр.

6) Закон Кулона. Напряженность электрического поля. Принцип суперпозиции. Поток электростатического поля. Коэффициент диэлектрической проницаемости. Вектор электрической индукции. Теорема Гаусса и её применение для расчета поля.

Закон Кулона

Два точечных заряда в вакууме действуют друг на друга с силами, которые пропорциональны произведению модулей этих зарядов, обратно пропорциональны квадрату расстояния между ними и направлены вдоль прямой, соединяющей эти заряды.

Напряженность электрического поля

Напряжённость электри́ческого по́ля — векторная физическая величина, характеризующая электрическое поле в данной точке и численно равная отношению силы действующей на пробный заряд, помещенный в данную точку поля, к величине этого заряда q:

.

Также иногда называется силовой характеристикой электрического поля.

Принцип суперпозиции

Принцип суперпозиции утверждает, что электростатический потенциал, создаваемый в данной точке системой зарядов, есть сумма потенциалов отдельных зарядов.

Поток электростатического поля

Число линий вектора E, пронизывающих некоторую поверхность S, называется потоком вектора напряженности N_E.

Коэффициент диэлектрической проницаемости

Диэлектрическая проницаемость среды - это физическая величина, которая характеризует степень ослабления поля и показывает, во сколько раз уменьшается напряженность электрического поля в однородном диэлектрике 

Вектор электрической индукции

Вектор электрической индукции (электрическое смещение) — векторная величина, равная сумме вектора напряжённости электрического поля и вектора поляризации.

Теорема Гауcca и ее применение для расчета поля.

Теорема Гаусса

Общая формулировка: Поток вектора напряжённости электрического поля через любую произвольно выбранную замкнутую поверхность пропорционален заключённому внутри этой поверхности электрическому заряду.

СГС	СИ

где

— поток вектора напряжённости электрического поля через замкнутую поверхность S.

Применение теоремы Гаусса к расчёту некотрых полей

 Поле равномерно заряженной бесконечной плоскости. Бесконечная плоскость (рис. 1) заряжена с постоянной поверхностной плотностью +σ (σ = dQ/dS — заряд, который приходится на единицу поверхности). Линии напряженности перпендикулярны данной плоскости и направлены от нее в каждую из сторон. Возьмем в качестве замкнутой поверхности цилиндр, основания которого параллельны заряженной плоскости, а ось перпендикулярна ей. Так как образующие цилиндра параллельны линиям напряженности поля (соsα=0), то поток вектора напряженности сквозь боковую поверхность цилиндра равен нулю, а полный поток сквозь цилиндр равен сумме потоков сквозь его основания (площади оснований равны и для основания Е_n совпадает с Е), т. е. равен 2ES. Заряд, который заключен внутри построенной цилиндрической поверхности, равен σS. Согласно теореме Гаусса, 2ES=σS/ε₀, откуда   (1)  Из формулы (1) следует, что Е не зависит от длины цилиндра, т. е. напряженность поля на любых расстояниях равна по модулю, иными словами, поле равномерно заряженной плоскости однородно.  Поле двух бесконечных параллельных разноименно заряженных плоскостей (рис. 2). Пусть плоскости заряжены равномерно разными по знаку зарядами с поверхностными плотностями +σ и –σ. Поле таких плоскостей будем искать как суперпозицию полей, которые создаваются каждой из плоскостей в отдельности. На рисунке верхние стрелки соответствуют полю от положительно заряженной плоскости, нижние — от отрицательно заряженной плоскости. Слева и справа от плоскостей поля вычитаются (поскольку линии напряженности направлены навстречу друг другу), значит здесь напряженность поля E=0. В области между плоскостями E = E₊ + E_- (E₊ и E_- находятся по формуле (1)), поэтому результирующая напряженность   (2)  Значит, результирующая напряженность поля в области между плоскостями описывается зависимостью (2), а вне объема, который ограничен плоскостями, равна нулю. 

 Поле равномерно заряженной сферической поверхности. Сферическая поверхность радиуса R с общим зарядом Q заряжена равномерно с поверхностной плотностью +σ. Т.к. заряд распределен равномернопо поверхности то поле, которое создавается им, обладает сферической симметрией. Значит линии напряженности направлены радиально (рис. 3). Проведем мысленно сферу радиуса r, которая имеет общий центр с заряженной сферой. Если r>R,ro внутрь поверхности попадает весь заряд Q, который создает рассматриваемое поле, и, по теореме Гаусса, 4πr²E = Q/ε₀ , откуда   (3)  При r>R поле убывает с расстоянием r по такому же закону, как у точечного заряда. График зависимости Е от r приведен на рис. 4. Если r'<R, то замкнутая поверхность не содержит внутри себя зарядов, значит внутри равномерно заряженной сферической поверхности электростатическое поле отсутствует (E=0). 

Поле объемно заряженного шара. Шар радиуса R с общим зарядом Q заряжен равномерно с объемной плотностью ρ (ρ = dQ/dV – заряд, который приходится на единицу объема). Учитывая соображения симметрии, аналогичные п.3, можно доказать, что для напряженности поля вне шара получится тот же результат, что и в случае (3). Внутри же шара напряженность поля будет иная. Сфера радиуса r'<R охватывает заряд Q'=(4/3)πr'³ρ . Поэтому, используя теорему Гаусса, 4πr'²E=Q'/ε₀=(4/3)πr'³ρ/ε₀ . Т.к. ρ=Q/(4/3πR³)) получаем  (4)  Значит, напряженность поля вне равномерно заряженного шара описывается формулой (3), а внутри его изменяется линейно с расстоянием r' согласно зависимости (4). График зависимости Е от r для рассмотренного случая показан на рис. 5. 

Поле равномерно заряженного бесконечного цилиндра (нити). Бесконечный цилиндр радиуса R (рис. 6) равномерно заряжен с линейной плотностью τ (τ = –dQ/dt заряд, который приходится на единицу длины). Из соображений симметрии мы видим, что линии напряженности будут направлены по радиусам круговых сечений цилиндра с одинаковой густотой во все стороны относительно оси цилиндра. Мысленно построим в качестве замкнутой поверхности коаксиальный цилиндр радиуса r и высотой l. Поток вектора Е сквозь торцы коаксиального цилиндра равен нулю (торцы и линии напряженности параллельны), а сквозь боковую поверхность равен 2πrlЕ. Используя теорему Гаусса, при r>R 2πrlЕ = τl/ε₀, откуда   (5)  Если r<R, то замкнутая поверхность внутри зарядов не содержит, поэтому в этой области E=0. Значит, напряженность поля вне равномерно заряженного бесконечного цилиндра задается выражением (5), внутри же его поле равно нулю. 

7) Работа электростатического поля. Потенциал электростатического поля и его связь с напряженностью .Циркуляция электростатического поля. Уравнение Максвелла электростатики.

Работа электростатического поля

Электрические силы совершают работу при перемещении пробного заряда q в точку пространства

На электрические заряды в электростатическом поле действуют силы. Поэтому, если заряды перемещаются, то эти силы совершают работу.

На заряд q, помещенный в однородное электрическое поле с напряженностью E, действует сила  . Работу поля можно рассчитать по формуле

где Δr⋅cos α = AC = x₂ – x₁ = Δx — проекция перемещения на силовую линию

Потенциал электростатическою поля и его связь с напряженностью

Электростатический потенциа́л (см. также кулоновский потенциал) — скалярная энергетическаяхарактеристика электростатического поля, характеризующая потенциальную энергию поля, которой обладает единичный заряд, помещённый в данную точку поля. Единицей измерения потенциала является, таким образом, единица измерения работы, деленная на единицу измерения заряда .

Электростатический потенциал — специальный термин для возможной замены общего термина электродинамики скалярный потенциал в частном случае электростатики (исторически электростатический потенциал появился первым, а скалярный потенциал электродинамики — его обобщение). Употребление термина электростатический потенциал определяет собой наличие именно электростатического контекста. Если такой контекст уже очевиден, часто говорят просто о потенциале без уточняющих прилагательных.

Электростатический потенциал равен отношению потенциальной энергии взаимодействия заряда с полем к величине этого заряда:

Напряжённость в какой-либо точке электрического поля равна градиенту потенциала в этой точке, взятому с обратным знаком. Знак «минус» указывает, что напряженность E направлена в сторону убывания потенциала.

Напряженность электрического поля и потенциал используются для описания электри­ческого поля. -векторная величина, - скалярная величина. Они связаны между собой. Установим эту связь. Для этого, (см. рис. 7), проведем две эквипотенциальные поверхности и . Как было показано выше перпендикулярна эквипотенциальной поверхности. Работа по перемещению пробного заряда q’ из точки с потенциалом в точку с потенциалом согласно формуле(10)

равна . С другой стороны . Таким образом , отсюда , (13) - характеризует быстроту изменения потенциала. В более общем случае , (14) где .

Градиент потенциала есть вектор, направленный по нормали к эквипотенциальной поверх­ности в сторону наибыстрейшего возрастания . Знак "минус" в (14) означает, что и направлены в противоположные стороны. Из формул (13), (14) следует, что напря­женность электрического поля Е измеряется в В/м.

Циркуляция электростатического поля

Теорема о циркуляции магнитного поля — одна из фундаментальных теорем классической электродинамики, сформулированная Ампером в 1826 году. В 1861 году Джеймс Максвелл снова вывел эту теорему, опираясь на аналогии с гидродинамикой, и обобщил ее (см. ниже). Уравнение, представляющее собой содержание теоремы в этом обобщенном виде, входит в число уравнений Максвелла. (Для случая постоянных электрических полей - то есть в принципе в магнитостатике - верна теорема в первоначальном виде, сформулированном Ампером и приведенном в статье первым; для общего случая правая часть должна быть дополнена членом с производной напряженности электрического поля по времени - см. ниже). Теорема гласит: Циркуляция магнитного поля постоянных токов по всякому замкнутому контуру пропорциональна сумме сил токов, пронизывающих контур циркуляции.

3.1.2. В неоднородном поле точечного заряда q (см. рис. 2 ) Найдем работу по перемещению пробного заряда q’ из точки 1 в точку 2 в поле, создаваемом точечным зарядом q:

. (2)

И в этом случае работа сил не зависит от формы пути. Она является только функцией начального и конечного положения заряда.

Для замкнутой траектории L она равна нулю, т. к. , т. е.

или (3)

Т. E. ЦИРКУЛЯЦИЯ ВЕКТОРА НАПРЯЖЕННОСТИ ПО ЛЮБОМУ ЗАМКНУТОМУ КОНТУРУ РАВНА НУЛЮ.

В механике было приведено следующее определение: "Силы, работа которых не зависит от формы пути, называются консервативными силами, а поля, работа сил которых не зави­сит от формы пути, называются потенциальными полями". Таким образом, рассмотренное нами электростатическое поле является потенциальным, а кулоновские силы - консерватив­ными.

Уравнения Максвелла в электростатике.

Основы теории Максвелла для электромагнитного поля

В 60-х годах прошлого века (около 1860 г.) Максвелл, основываясь на идеях Фарадея, обобщил законы электростатики и электромагнетизма: теорему Гаусса - Остроградского для электростатического поля и для магнитного поля ; закон полного тока ; закон электромагнитной индукции , и в результате разработал законченную теорию электромагнитного поля.

Теория Максвелла явилась величайшим вкладом в развитие классической физики. Она позволила с единой точки зрения понять широкий крут явлений, начиная от электро­статического поля неподвижных зарядов и заканчивая электромагнитной природой света.

Математическим выражением теории Максвелла служат четыре уравнения Максвелла. которые принято записывать в двух формах: интегральной и дифференциальной. Дифференциальные уравнения получаются из интегральных с помощью двух теорем вектор ного анализа - теоремы Гаусса и теоремы Стокса. Теорема Гаусса:

(1)

(2)

- проекции вектора на оси; V - объем, ограниченный поверхностью S.

Теорема Стокса: . (3)

здесь rot - ротор вектора , который является вектором и выражается в декартовых коор­динатах следующим образом: rot , (4)

S - площадь, ограниченная контуром L.

Уравнения Максвелла в интегральной форме выражают соотношения, справедливые для мысленно проведенных в электромагнитном поле неподвижных замкнутых контуров и поверхностей.

Уравнения Максвелла в дифференциальной форме показывают как связаны между собой характеристики электромагнитного поля и плотности зарядов и токов в каждой точке этого поля.

12.1. Первое уравнение Максвелла

Оно является обобщением закона электромагнитной индукции ,

и в интегральной форме имеет следующий вид (5)

и утверждает.что с переменным магнитным полем неразрывно связано вихревое электри­ческое поле , которое не зависит оттого находятся в нем проводники или нет. Из (3) следует, что . (6)

Из сравнения (5) и (6) находим, что (7)

Это и есть первое уравнение Максвелла в дифференциальной форме.

12.2. Ток смешения. Второе уравнение Максвелла

Максвелл обобщил закон полного тока предположив, что переменное электрическое поле, также как и электрический ток, является источником магнитно­го поля. Для количественной характеристики "магнитного действия" переменного электри­ческого поля Максвелл ввел понятие тока смещения.

По теореме Гаусса - Остроградского поток электрического смешения сквозь замкну­тую поверхность

Продифференцировав это выражение по времени, получим для неподвижной и недеформирусмой поверхности S (8)

Левая часть этой формулы имеет размерность тока, который как известно, выражает­ся через вектор плотности тока . (9)

Из сравнения (8) и (9) следует, что имеет размерность плотности тока: А /м². Максвелл предложил назвать плотностью тока смещения:

. (10)

Ток смещения . (11)

Из всех физических свойств, присущих действительному току (току проводимости), связанному с переносом зарядов, ток смешения обдададает лишь одним: способностью соз­давать магнитное поле. При "протекании" тока смещения в вакууме или диэлектрике не вы­деляется тепло. Примером тока смещения может служить переменный ток через конденсатор. В общем случае токи проводимости и смещения не разделены в пространстве и мож­но говорить о полном токе, равном сумме токов проводимости и смещения: (12)

С учетом этого Максвелл обобщил закон полного тока, добавив в правую часть его ток смешения . (13)

Итак, второе уравнение Максвелла в интегральной форме имеет вид:

. (14)

Из (3) следует, что . (15)

Из сравнения (14) и (15) находим, что . (16)

Это и есть второе уравнение Максвелла в дифференциальной форме.

12.3. Третье и четвертое уравнения Максвелла

Максвелл обобщил теорему Гаусса - Остроградского для электростатического поля. Он предположил, что эта теорема справедлива для любого электрического поля, как стационарного, так и переменного. Соответственно, третье уравнение Максвелла в интегральной форме имеет вид: . (I7) или . (18)

где - объемная плотность свободных зарядов, [ ] = Кл / м³

Из (1) следует, что . (19)

Из сравнения (18) и (19) находим,что . (20)

Четвертое уравнение Максвелла в интегральной и дифференциальной формах имеет

следующий вид: , (21) . (22)