- •1. Цели дисциплины «Сопротивление материалов»
- •7. Растяжение и сжатие. Общие понятия.
- •8. Напряжения и перемещения. Закон Гука
- •9. Механические характеристики и свойства материалов
- •10. Допускаемые напряжения и запасы прочности
- •Запас прочности.
- •Коэффициент запаса.
- •11. Расчеты на прочность и жесткость статически определимых и статически неопределимых систем
- •12. Влияние собственного веса при растяжении и сжатии
- •13. Напряженное состояние при растяжении и сжатии
- •14. Напряжения в наклонных площадках при плоском и объемном напряженных состояниях. Обобщенный закон Гука
- •Частные случаи плоского напряженного состояния
- •Обобщенный закон Гука
- •15. Изгиб прямолинейного бруса. Общие понятия.
- •Построение эпюр поперечной силы и изгибающего момента
- •16. Типы опор и определение опорных реакций
- •17. Поперечная сила и изгибающий момент
- •18. Геометрические характеристики плоских сечений Общие сведения
- •Прямоугольник
- •Треугольник
- •19. Напряжения при изгибе. Расчеты на прочность
- •20. Определение перемещений при изгибе. Расчет на жесткость.
- •21. Кручение. Чистый сдвиг и его особенности
- •22. Кручение стержня круглого поперечного сечения
- •23. Расчеты на прочность и жесткость при кручении.
- •24. Напряженное состояние и разрушение при кручении.
- •Построение эпюр крутящих моментов
- •Рациональная форма сечения вала
- •Деформации при кручении и условие жесткости
- •25. Сложное сопротивление. Общие понятия.
- •Косой изгиб призматического стержня Совместное действие изгиба и растяжения или сжатия Внецентренное сжатие или растяжение.
- •26. Теории прочности.
- •Критерии разрушения
- •Гипотеза наибольших линейных деформаций (II теория прочности, Мариотт, 1682 г.)
- •Критерии пластичности
- •Гипотеза наибольших касательных напряжений (III теория прочности; Кулон, 1773 год)
- •Теория наибольшей удельной потенциальной энергии формоизменения (IV теория прочности; Бельтрами - 1885 г.; Губер - 1904 г.)
- •Теория прочности Мора (V теория прочности)
- •Замечания о выборе теории прочности
- •27. Кручение с изгибом.
- •28. Косой изгиб.
- •29. Внецентренное растяжение-сжатие.
- •30. Устойчивость сжатых стержней (продольный изгиб). Основные понятия.
- •31. Формула Эйлера – вывод, предел применимости.
- •32. Эмпирические формулы для определения критических напряжений. Проверка сжатых стержней на устойчивость.
- •33. Понятие о динамических нагрузках. Удар. Основные понятия.
- •34. Горизонтальный удар.
- •35. Вертикальный удар. Удар от внезапной остановки движения.
- •36. Колебания систем с одной степенью свободы.
12. Влияние собственного веса при растяжении и сжатии
Если
ось в стержне вертикальна, то его
собственный вес вызывает центральное
растяжение или сжатие. Если вертикальный
брус закреплен верхним концом, то от
собственного веса он растягивается, а
при закреплении нижнего конца - сжимается.
Собственный вес вертикального бруса
можно рассматривать как продольную
(осевую) внешнюю нагрузку, распределенную
вдоль оси бруса.
Рассмотрим
брус постоянного сечения, закрепленный
верхним концом. Продольная сила от
собственного веса в поперечном сечении
бруса на расстоянии х от
его нижнего конца равна весу нижележащей
части
бруса:
![]() (1.4)
где
Nx -
продольная сила от собственного веса,
Н;
(1.4)
где
Nx -
продольная сила от собственного веса,
Н;
![]() -
плотность материала, кг/м3;
g -
ускорение свободного падения, м/с2;
А -
площадь поперечного сечения бруса,
м2;
х -
расстояние от нижнего конца стержня,
м.
Напряжение
от собственного веса определяется по
формуле:
-
плотность материала, кг/м3;
g -
ускорение свободного падения, м/с2;
А -
площадь поперечного сечения бруса,
м2;
х -
расстояние от нижнего конца стержня,
м.
Напряжение
от собственного веса определяется по
формуле:
![]() (1.5)
По
формулам (1.4) и (1.5) строятся эпюры N и
(1.5)
По
формулам (1.4) и (1.5) строятся эпюры N и ![]() с
учетом знаков. Если на стержень действует
дополнительная сила F,
то продольная сила и нормальное напряжение
определяются по
формулам:
с
учетом знаков. Если на стержень действует
дополнительная сила F,
то продольная сила и нормальное напряжение
определяются по
формулам:
![]() (1.6)
(1.6)
![]() (1.7)
Полное
удлинение (укорочение) стержня постоянного
сечения от собственного веса определяется
по
формуле:
(1.7)
Полное
удлинение (укорочение) стержня постоянного
сечения от собственного веса определяется
по
формуле:
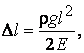 (1.8)
где
l-
длина стержня, м;
Е -
модуль продольной упругости материала,
Па.
При
действии внешней силы Fи
собственного веса удлинение
стержня
определяется
по формуле:
(1.8)
где
l-
длина стержня, м;
Е -
модуль продольной упругости материала,
Па.
При
действии внешней силы Fи
собственного веса удлинение
стержня
определяется
по формуле:
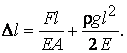 (1.9)
В
формулах (1.7), (1.9) физический смысл первого
слагаемого - напряжение и удлинение от
внешней силы, второго - напряжение и
удлинение от собственного веса.
Перемещение
любого поперечного сечения бруса,
закрепленного верхним концом, равно
удлинению части бруса, лежащей над
сечением и равно сумме удлинений под
действием собственного веса верхней
части, нижней части бруса и внешней
силы.
(1.9)
В
формулах (1.7), (1.9) физический смысл первого
слагаемого - напряжение и удлинение от
внешней силы, второго - напряжение и
удлинение от собственного веса.
Перемещение
любого поперечного сечения бруса,
закрепленного верхним концом, равно
удлинению части бруса, лежащей над
сечением и равно сумме удлинений под
действием собственного веса верхней
части, нижней части бруса и внешней
силы.
13. Напряженное состояние при растяжении и сжатии
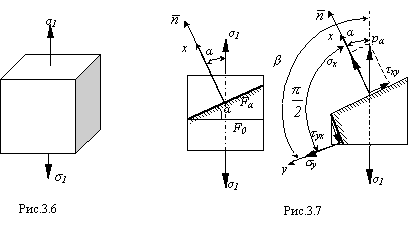
Линейным или одноосным называется напряженное состояние, при котором два из трех главных напряжений равны нулю (рис.3.6).
Примером линейного напряженного состояния может служить осевое растяжение-сжатие.
Рассмотрим задачу определения напряжений
в площадке общего положения. Угол наклона
этой площадки ![]() будем
отмерять от направления
будем
отмерять от направления ![]() до
нормали к площадке
до
нормали к площадке ![]() .
Примем, что положительный угол
откладывается
против хода часовой стрелки, а отрицательный
по ходу часовой стрелки. Направим
ось х вдоль нормали
,
ось у – перпендикулярно
ей.
.
Примем, что положительный угол
откладывается
против хода часовой стрелки, а отрицательный
по ходу часовой стрелки. Направим
ось х вдоль нормали
,
ось у – перпендикулярно
ей.
|
|
Для определения напряжений ![]() и
и ![]() рассмотрим
рис.3.7.
рассмотрим
рис.3.7.
Получим:
![]()
где ![]() -
площадь наклонной площадки,
-
площадь наклонной площадки,
![]() -
площадь поперечного сечения,
-
площадь поперечного сечения,
![]() -
полное напряжение, действующее по
наклонной площадке.
-
полное напряжение, действующее по
наклонной площадке.
Учитывая, что ![]() ,
получим:
,
получим:
![]() .
.
Раскладывая ![]() на
направление оси х и оси у,
получим
на
направление оси х и оси у,
получим
![]() ,
,
![]() .
.
Рассмотрим площадку ![]() перпендикулярную
площадке
,
угол
перпендикулярную
площадке
,
угол ![]() .
Направим ось y по
нормали к этой площадке. Нормальные
напряжения, действующие по этой площадке
равны
.
Направим ось y по
нормали к этой площадке. Нормальные
напряжения, действующие по этой площадке
равны
![]() .
.
Складывая
и ![]() ,
получим
,
получим
![]() ,
,
т.е. сумма нормальных напряжений по двум взаимно перпендикулярным площадкам величина постоянная и равна главному напряжению.
Касательные напряжения, действующие по наклонной площадке
![]() ,
,
т.е. справедлив закон парности касательных напряжений.
Нормальные напряжения
по
наклонной площадке
достигают
максимального значения ![]() при
при ![]() ,
т.е. в поперечном сечении.
,
т.е. в поперечном сечении.
Касательные напряжения
по
наклонной площадке
достигают
максимального значения ![]() при
при ![]() .
.