Теория прочности Мора (V теория прочности)

Теория прочности Мора позволяет учесть различие в свойствах материалов при растяжении и сжатии. Ее можно получить путем модификации теории наибольших касательных напряжений в соответствии с уравнением:

                                                                                                                                                          (7.35)

При одноосном сжатии в предельном случае s₁=0, s₃=–σ_т^с

                                                                                                                                               (7.36)

откуда определяется коэффициент k

                                                                                                                                                                           (7.37)

для пластичных материалов, или

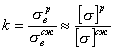                                                                                                                                                                            (7.38)

для хрупких материалов.

Условие прочности по теории Мора имеет следующий вид:

                                                                                                                                                        (7.39)

Замечания о выборе теории прочности

Обзор многочисленных теорий предельных состояний показывает, что совершенных теорий еще нет. Каждая из существующих теорий справедлива только в определенных условиях и для определенных материалов. Рассмотренными выше теориями можно пользоваться только при напряженных состояниях с главными напряжениями разных знаков. Возможность применения этих теорий в случаях трехосного растяжения или сжатия требует дополнительной экспериментальной проверки.

При выборе теории прочности в случае плоского напряженного состояния и объемного напряженного состояния с главными напряжениями разных знаков надо учитывать свойства материала. Если материал пластичен и одинаково работает на растяжение и сжатие, то следует пользоваться теорией наибольшей энергии формоизменения или теорией максимальных касательных напряжений. Если пластичный материал неодинаково сопротивляется растяжению и сжатию, то следует применить теорию Мора. Расчет хрупких материалов при указанных напряженных состояниях следует производить по теории Мора.

27. Кручение с изгибом.

Для использования основных расчетных формул, использующих эквивалентные напряжения, необходимо определить главные нормальные напряжения. (Три главные напряжения определяются кубическим уравнением, точные решения которого даются формулами Кордано). 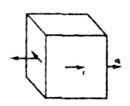 Рис. 7.3  Однако в частном, но часто встречающемся случае плоского напряженного состояния, когда имеется совместное кручение и изгиб (или растяжение), возникает напряженное состояние, показанное на рис. 7.3  В этом случае максимальное и минимальное напряжения определяются формулой: Следовательно, учитывая, что  , главные нормальные напряжения будут следующими: 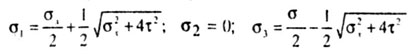 при этом эквивалентные напряжения примут вид: по теории наибольших касательных напряжений (3-я теория) по энергетической теории (4-я теория) по теории Мора (5-я теория) 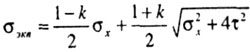Сравнивая выражения для эквивалентных напряжений по теории наибольших касательных напряжений и энергетической теории, при  >  , что и имеет место в большинстве случаев, обе теории дают близкие друг к другу результаты. Для стержней круглого поперечного сечения, для которых момент сопротивления кручению Wk в два раза больше момента сопротивления изгибу Wизг: Wk = 2W, при воздействии на них изгибающего М и крутящего Мk моментов, последние три формулы принимают соответствующивй вид: 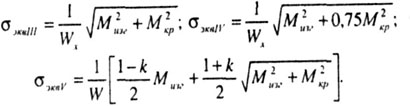Практические расчеты на прочность по допускаемым напряжениям при сложном напряженном состоянии ведутся, как правило, с использованием формулы Мора. Для хрупких материалов хорошее соответствие с опытом дали теории прочности, когда разрушение идет по схеме отрыва. Если же материал обладает одинаковыми механическими характеристиками при растяжении и сжатии (к = 1), то можно применить формулы гипотез наибольшего касательного напряжения и энергии формоизменения. 

Порядок выполнения расчета

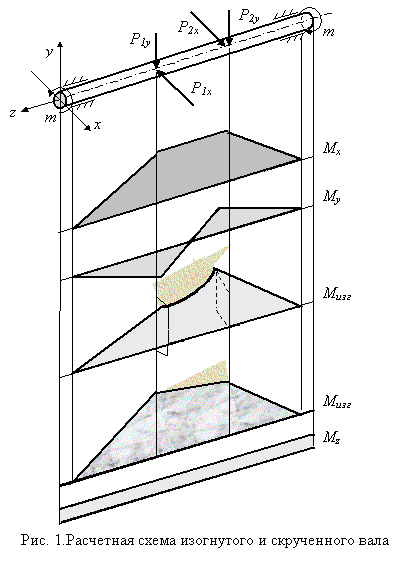
Исследуем этот вид деформации стержня на примере расчета вала кругового (кольцевого) поперечного сечения на совместное действие изгиба и кручения (рис. 1).

Примем следующий порядок расчета.

1. Разлагаем все внешние силы на составляющие

P_1x, P_2x, ... , P_nx и P_1y, P_2y, ... , P_ny

2. Строим эпюры изгибающих моментов M_y и M_y. от этих групп сил.

У кругового и кольцевого поперечного сечений все центральные оси главные, поэтому косого изгиба у вала вообще не может быть, следовательно, нет смысла в каждом сечении иметь два изгибающих момента Mx, и My а целесообразно их заменить результирующим (суммарным) изгибающим моментом

который вызывает прямой изгиб в плоскости его действия относительно нейтральной оси n-n, перпендикулярной вектору М_изг. Эпюра суммарного момента имеет пространственное очертание и поэтому неудобна для построения и анализа. Поскольку все направления у круга с точки зрения п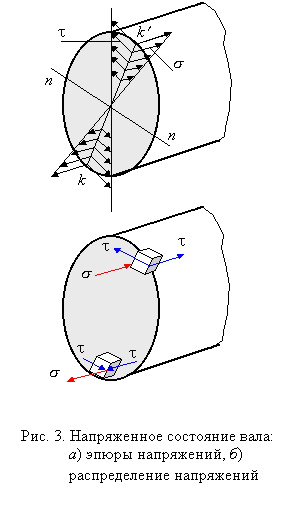 рочности равноценны, то обычно эпюру М_изг спрямляют, помещая все ординаты в одну (например, вертикальную) плоскость. Обратим внимание на то, что центральный участок этой эпюры является нелинейным.

3. Строится эпюра крутящего момента М_z.

Наибольшие напряжения изгиба возникают в точках k и k', наиболее удаленных от нейтральной оси (рис. 3),

где W_изг - момент сопротивления при изгибе.

В этих же точках имеют место и наибольшие касательные напряжения кручения

где W_р - момент сопротивления при кручении.

Как следует из рис. 3, напряженное состояние является упрощенным плоским (сочетание одноосного растяжения и чистого сдвига). Если вал выполнен из пластичного материала, оценка его прочности должна быть произведена по одному из критериев текучести. Например, по критерию Треска-Сен-Венана имеем

Учитывая, что W_р=2W_изг, для эквивалентных напряжений получаем

где   - эквивалентный момент, с введением которого задача расчета вала на совместное действие изгиба и кручения, сводится к расчету на эквивалентный изгиб.

Аналогично для М_экв по критерию Губера-Мизеса получаем

Тогда условие прочности для вала из пластичного материала будет иметь вид

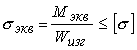
Для стержня из хрупкого материала условие прочности следует записать в виде

где М_экв должен быть записан применительно к одному из критериев хрупкого разрушения. Например, по критерию Мора

где m = [_p] / [_c].

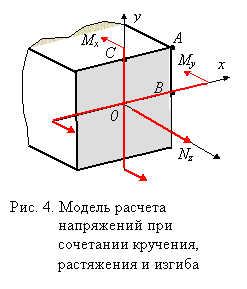
Обратим внимание на особенности расчета при сочетании изгиба, растяжения и кручения стержня прямоугольного поперечного сечения (рис. 4). Для выявления опасной точки здесь должны быть сравнены напряжения косого изгиба с растяжением в точке А, с эквивалентными напряжениями в точках В и С.

Полученные соотношения приобретают крайнюю необходимость и востребованность при выполнении Вами курсового проекта по основам конструирования при расчете на прочность и жесткость валов передач.