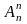- •1.Предмет и задачи дм. Дискр величины.
- •2.Понятие рекурсии. Показ принципа работы рекурсии на схеме.
- •4.Система рекуррентных соотношений
- •5. Приемы и методы решения рекуррентных соотношений.
- •6.Предмет и задачи раздела раздела матем-ки комбинаторика. Правили суммы и правило произведения.
- •7.Комбинаторика. Размещение с повторением и без повторения.
- •8.Комбинаторика. Перестановка с повтор-ем и без повтор-я.
- •9. Комбинаторика. Сочетание с повторением и сочетание без повторения
- •10. Комбинаторные задачи геом-ого содержания. Свойства чисел . Свойства чисел
- •13. Генерация подмножеств. Числа Стирлинга 2-го и 1-го рода.
- •14. Числа Каталана.
- •15. Полиномиальная формула.
- •16. Производящие функции и их применения.
- •17. Принцип включения и исключения.
- •18. Функция Эйлера. Функция Мебиуса.
- •19. Графы. Основные понятия и определения теории графов.
- •20. Матрица смежности. Валентность вершины. Матрица инцидентности.
- •21. Виды графов
- •22. Маршруты, цепи(пути) и циклы в графах.
- •23. Связные графы. Изоморфизм графов. Подграфы.
- •24. Эйлеровы и гамильтоновы графы.(Эйлеров граф).
- •25. Изоморфизм графов.
- •26. Планарные графы. Непланарность графов к5 и к3,3. Теорема Понтрягина-Куротовского.
- •27. Теорема Эйлера и ее следствия.
- •28. Деревья.
- •29. Ориентированные графы. Полный ориентированный граф.
- •30. Графы с цветными ребрами. Свойства графов с цветными ребрами.
- •31. Сетевое планирование и управление. Сетевой график.
- •32. Принципы и правила построения сетевых графиков.
- •33. Критический путь в сетевых графиках.
- •34. О резервах времени в сетевых графиках.
14. Числа Каталана.
Числом Каталана наз-ся число различных скобочных структур из n пар скобок.
Если =1, то последовательность чисел К. равна: 1,1,3,5,14,42,132,…
Применение чисел Каталана.
Числа К. перечисляют самые разнообразные комбинаторные объекты. Реализация чисел К. осуществляется диагональной триангуляцией(это разбиение многоугольника на треугольники непересекающимися диагоналями).Еще одна важная реализация чисел К. связана с путями Дика на плоскости (путем Дика называется непрерывная ломанная в верхней полуплоскости, составленная из векторов (1,1) и (1,-1),начинающаяся в начале координат и заканчивающаяся на оси абсцисс). Совершенно ясно, как устанавливается соответствие между путями Дика и правильными скобочными структурами : нужно сопоставить вектору (1,1) левую скобку, а вектору (1,-1) правую. Тогда условие, что путь лежит в верхней полуплоскости и заканчивается на оси абсцисс, и есть в точности условие правильности скобочной структуры. Поэтому число путей Дика из 2n звеньев равно n-му числу Каталана .
15. Полиномиальная формула.
Вывод формулы бинома Ньтона можно получить и др. способом.
Для этого запишем
(a+b)n=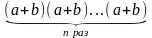 .
раскроем скобки выписывая многочлены
в порядке их появления.
.
раскроем скобки выписывая многочлены
в порядке их появления.
(a+b)2=aa+ba+ab+bb
(a+b)3=aaa+aab+aba+abb+baa+bab+bba+bbb
……………………………………………….
Ясно, что слагаемые в правой части будут произведениями всевозможных перестановок с повторениями длины n из букв a и b, чтобы привести подобные члены нежно найти число перестановок имеющих заданный состав (n1;n2) n1+ n2=n.
Т.е. это есть ничто
иное как P(n1,n2)
тогда получим суммы слагаемых вида
P(n1,n2)
an1
bn2.
И окончательно (a+b)n= (1)
(1)
Чтобы привести
наше равенство (1) к более привычной нам
формуле
 (2)
(2)
достаточно положить,
что n2=k,
n1=n-k,

Произведенные доказательства переносятся на случай нескольких слагаемых.
 (3)
(3)
Формула (3) носит название полиномиальной формулы.
16. Производящие функции и их применения.
В комбинаторном анализе для доказательства различных соотношений широко используется т.к. методы производящих функций.
Производящие функции определяются для последовательностей. Пусть дана конечная или бесконечная последовательность а0,а1, а2,…, аk. Производящей функцией этой последовательности называется формула A(x)= а0+а1x+ а2x2+…+ аkxk+…
Экспотенциальной
производящей функцией называется
функция

Если последовательность конечна, то производящие функции определяются конечными суммами.
Если последовательность бесконечна, то производящие функции определяются бесконечными рядами, при этом часто пользуются такими функциями и даже в тех случаях когда соответствующие ряды расходятся.
Для последовательности чисел сочетаний из k элементов (без повторений) производящей функцией будет
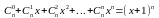
Экспотенциальной
производящей формулой для размещений
(без повторений) будет