- •1.Предмет и задачи дм. Дискр величины.
- •2.Понятие рекурсии. Показ принципа работы рекурсии на схеме.
- •4.Система рекуррентных соотношений
- •5. Приемы и методы решения рекуррентных соотношений.
- •6.Предмет и задачи раздела раздела матем-ки комбинаторика. Правили суммы и правило произведения.
- •7.Комбинаторика. Размещение с повторением и без повторения.
- •8.Комбинаторика. Перестановка с повтор-ем и без повтор-я.
- •9. Комбинаторика. Сочетание с повторением и сочетание без повторения
- •10. Комбинаторные задачи геом-ого содержания. Свойства чисел . Свойства чисел
- •13. Генерация подмножеств. Числа Стирлинга 2-го и 1-го рода.
- •14. Числа Каталана.
- •15. Полиномиальная формула.
- •16. Производящие функции и их применения.
- •17. Принцип включения и исключения.
- •18. Функция Эйлера. Функция Мебиуса.
- •19. Графы. Основные понятия и определения теории графов.
- •20. Матрица смежности. Валентность вершины. Матрица инцидентности.
- •21. Виды графов
- •22. Маршруты, цепи(пути) и циклы в графах.
- •23. Связные графы. Изоморфизм графов. Подграфы.
- •24. Эйлеровы и гамильтоновы графы.(Эйлеров граф).
- •25. Изоморфизм графов.
- •26. Планарные графы. Непланарность графов к5 и к3,3. Теорема Понтрягина-Куротовского.
- •27. Теорема Эйлера и ее следствия.
- •28. Деревья.
- •29. Ориентированные графы. Полный ориентированный граф.
- •30. Графы с цветными ребрами. Свойства графов с цветными ребрами.
- •31. Сетевое планирование и управление. Сетевой график.
- •32. Принципы и правила построения сетевых графиков.
- •33. Критический путь в сетевых графиках.
- •34. О резервах времени в сетевых графиках.
7.Комбинаторика. Размещение с повторением и без повторения.
Камбинаторика- одна из разделов ДМ, котор приобрел важн значения в связи с использов-ем его в теории вероятности, матем логики, теор чисел, вычислит техники, кибернетики и т.д и т.п. Комбинаторику м\о рассм как часть теории конечн мн-в, любую комбинаторную задачу м\о свести к задаче о конечных множ-вах и их отображениях.
а)Размещ-е с
повторением
Опр-е:
Картежи длины k
составлены
из m
эл-го мн-ва x,
назыв
размещениямис повторениями из m
эл-ов по k.
Обознач
 .
А-«arrangement»-
размещение.
.
А-«arrangement»-
размещение.
 =mk
=mk
б)Размещ-е без
повторений Опр-е:
Упорядочен мн-ва длины k
составл из эл-ов m
эл-го мн-ва x
назыв размещениями без повторений из
m
эл-ов мн-ва x
по k.

Опр-е: k
элем-ые подмнож-ва m
эл-го подмнож-ва x
назыв сочет-ми без повторений из эл-ов
этого мн-ва по k.
Обознач его Сkm

8.Комбинаторика. Перестановка с повтор-ем и без повтор-я.
а) Переест без повтор: Если длина размещения без повторений равна числу m элем-ов мн-ва x (в размещении учавств все эл-ты), то в таком размещении встречаются по одному разу все эл-ты x. 2 таких размещения отличаются др от др только лишь порядком эл-ов.
Опр-е: Перестановкой без повторений из m эл-ов обознач Pm(permutation- перестановка) назыв размещение без повторений из этих эл-ов по m Pm=m!
Вывод ф-лы:Рm=m· (m-1) · (m-2)…3·2·1=m!
б)Переест
с повтор: Найти
число картежей котор м\о получить
переставляя компоненты данного картежа.
Чтобы уточнить постановку задачи введем
понятие состав кортежа. Пусть а-кортеж
длины n
состав из эл-ов m-эл-го
мн-ва x={x1,x2,…,xm}.
Кажд числу k(1≤k≤m)
соотв число nk
показывающ
ск-ко раз
эл-т xk
встречается среди компонент картежей
а.
Выписывая по порядку эти числа получ
новые картеж (n1,n2,n3,….nm)
котор наз-ся составом картежа
x={x1,x2,x3,x4}
a={x1,
x3,
x1,
x4
,x3,
x1}
2 картежа им один и тотже состав, могут
отличаться др от др лишь порядком
компонент, их назыв перестаноками с
повторениями данного состава.
P(n1,n2,n3,…,nm)=
9. Комбинаторика. Сочетание с повторением и сочетание без повторения
Сочетания без повторений
k – элементные подмножества m – элементного множества Х называют сочетаниями без повторения из элементов этого множества по k.
Вывод ф-лы:
В тех сл-ях когда нас не интересует порядок эл-в в расстановке, и интересует лишь ее состав, то говорят о сочетаниях.
Соч-ми
из m
различных эл-в по k,
называют всевозможные расстановки
длины k,
обр-е из этих эл-в и отличающихся др. от
др. составом, но не порядком эл-в.

Составим все
сочетания из m
по k,
затем переставим в каждом сочетании
эл-ты всеми возм-ми способами, теперь
мы получим расстановки отличающиеся
либо сост., либо порядком, т.е. это все
размащения без повтор. из m
по k
( ).
).
учитывая, что
каждое сочетание дает k!
размещений, то по правилу пр-я получим,
что


Сочетания с повторением
Найдем число
различных составов, которые могут иметь
кортежи длины n,
состоящие из элементов множества Х,
содержащего m
элементов. Каждый такой состав является
картежом состоящим из m
чисел ( )
таких, что
)
таких, что
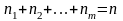 .
Его можно записать в виде кортежа из 0
и 1, заменив каждое число соответствующим
числом 1 и подставив 0 после каждой
группы единиц кроме последней.
.
Его можно записать в виде кортежа из 0
и 1, заменив каждое число соответствующим
числом 1 и подставив 0 после каждой
группы единиц кроме последней.
exe: вместо картежа (4,2,1) можно записать: 1,1,1,1,0,1,1,0,1 или (2,0,0,3) – 1,1,0,0,0,1,1,1.
Число единиц входящие в последний кортеж = , а число 0 равно m-1, поэтому число различных кортежей такого вида равно числу перестановок с повторениями из n единиц и m-1 нулей P(n,m-1).
Опр.: Различное число картежей длины n, компоненты которых принадлежат данному m-элементному множеству Х называют также сочетаниями с повторениями из m по n.