14.Операции над комплексными числами в алгебраической форме и их свойства.

Алгебраическая форма комплексных чисел (рис. 5.1)       Обозначения, терминология 

где i - мнимая единица; a - действительная часть: a = Re z; bi - мнимая часть: b = Im z; числа видаbi - чисто мнимые; плоскость Oxy - комплексная плоскость; ось Ох - действительная ось; ось Oy - мнимая ось;

       - число, сопряженное числу z = a + bi;

       - модуль комплексного числа;   либо  , - аргумент комплексного числа z (главное значение аргумента);

Arg z - множество аргументов числа z:

     Действия над комплексными числами 

     Если   то:

Действия с комплексными числами, заданных в алгебраической форме

Свойство сложени: Сумма двух комплексных чисел z1=a+bi и z2=c+di будет комплексное число вида z=z1+z2= a+bi + c+di = (a + c) + (b + d)i. 

Пример:  5+3i + 3−i =8+2i 

Свойство вычитания: Разность двух комплексных чисел z1=a+bi и z2=c+di будет комплексное число вида z=z1−z2= a+bi − c+di = a−c +(b−d)i 

Пример: .  5+3i − 3−i =2+4i 

Свойство умножения: Произведение двух комплексных чисел z1=a+bi и z2=c+di будет комплексное число вида z=z1 z2= a+bi c+di = ac−bd +(ad+bc)i 

Пример:  3+2i 4−i =12−3i+8i−2i2=14+5i 

Свойство деления: Частное двух комплексных чисел z1=a+bi и z2=c+di будет комплексное число видаz=z1/z2=a +bi/ c+di = ac+bd /c^2+d^2+ bc−ad/ c^2+d^2 * i

Степени мнимой единицы

i0=1  i3=−i  i6=−1  i4n=1 

i1=i i4=1  i7=−i  i4n+1=i

i2=−1  i5=i ....

15.Геометрическая интерпретация комплексных чисел. Геометрический смысл операций сложения и вычитания.

Геометрическая интерпретация комплексного числа

Всякое комплексное число z = (x, y) можно изобразить как точку на плоскости с координатами x иy. Плоскость, на которой изображаются комплексные числа, называется комплексной плоскостью, при этом ось Ox называется действительной, а Oy - мнимой.

Расстояние r точки z от нулевой точки, т. е. число

называется модулем комплексного числа z и обозначается символом |z|.

Число

называем аргументом комплексного числа z и обозначаем символом θ = arg z. При заданном rуглы, отличающиеся на  , соответствуют одному и тому же числу. В этом случае записываем   называем главным значением аргумента.

Числа r и θ называют полярными координатами комплексного числа z. В этом случае

z = (x, y) = (r cos θ, r sin θ) = r(cos θ + i sin θ)

называется тригонометрической формой комплексного числа.

Если z₁ = (r₁ cos θ₁, r₁ sin θ₁), z₂ = (r₂ cos θ₂, r₂ sin θ₂), то

z₁z₂ = (r₁r₂ cos(θ₁ + θ₂), r₁r₂ sin(θ₁ + θ₂)),

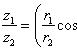
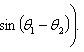
Для n-й степени числа z = (r cos θ, r sin θ) формула приобретает вид zⁿ = (rⁿ cos nθ, rⁿ sin nθ).

При r = 1 соотношение приобретает вид zⁿ = (cos nθ, sin nθ) и называется формулой Муавра.

Корень n-й степени из комплексного числа z имеет n различных значений, которые находятся по формуле

     (1)

П

П

П

П

П

П

16.Тригонометрическая форма записи комплексного числа. Умножение и деление комплексных чисел, записанных в тригонометрической форме. Геометрический смысл умножения комплексных чисел.