Доказательство

Возьмем произвольное фиксированное число x   (a,b).

По условию теоремы

Следовательно, в малой окрестности числа x₀ можно определить функцию α = α(Δx), стремящуюся к нулю при   такую, что

Но тогда   и, следовательно, функция f непрерывна при x = x₀. Так как число x₀ – произвольное, то функция fнепрерывна на всем интервале (a, b).

Теорема доказана.

Из доказанной теоремы непосредственно вытекает, что в точках разрыва функция не может быть дифференцируемой.

Однако из непрерывности функции на интервале (a, b) не следует дифферецируемость функции в каждой точке интервала (a, b). Например, функция   непрерывна на всей числовой прямой, но эта функция недифференцируема при x = 0. В самом деле, предел (1) не зависит от знака приращения аргумента Δx. Для функции же   имеем, если x = 0придать приращение Δx > 0, то Δy = Δx, а если Δx < 0, то Δy = − Δx. Таким образом,

Следовательно, функция   недифференцируема при x = 0.

5.Производная суммы, произведения, частного двух функций

Производная суммы (разности) функций

Производная алгебраической суммы функций выражается следующей теоремой.

Производная суммы (разности) двух дифференцируемых функций равна сумме (разности) производных этих функций:

Производная конечной алгебраической суммы дифференцируемых функций равна такой же алгебраической сумме производных слагаемых. Например,

Производная произведения функций.

Пусть u(x) и u(x) - дифференцируемые функции. Тогда произведение функций u(x)v(x) также дифференцируемо и

Производная произведения двух функций не равана произведению производных этих функций.

Производная частного функций.

Пусть u(x) и u(x) - дифференцируемые функции. Тогда, если v(x) ≠ 0, то производная частного этих функций вычисляется по формуле

6.Понятие сложной функции.

Понятие сложной функции

Пусть функция z = f(x,y) определена в некоторой окрестности точки (x₀, y₀) . Пусть ее аргументы x и y в свою очередь являются функциями x = x(t) , y = y(t) и определены в некоторой окрестности точки t₀ , причем x(t₀) = x₀ , y(t₀) = y₀ .

Тогда в окрестности точки t₀ определена сложная функция аргумента t

z = f(x(t), y(t)).

Аналогично определяется сложные функции любого числа переменных.

Например, если x и y — функции 2–х переменных: x = x(u,v) и y = y(u,v) , то функция z = f(x,y) является сложной функцией двух переменных u и v :

	z = f(x(u,v), y(u,v)).

Дифференцирование сложной функции.

Рассмотрим функцию y = sin x².  Чтобы найти значение этой функции в фиксированнной точке x нужно: 1) вычислить x²; 2) найти значение синуса от полученного значения x².  Иными словами, сначала надо найти значение g(x) = x², а потом найти sin g(x).  В подобных случаях говорят, что задана сложная функция y = f(g(x)).  В нашем примере u = g(x) = x², а y = f(u) = sin u.

Правило вычисления производной сложной функции.

Правило вычисления производных

Если функции f и g имеют конечные производные при  , то:

1)   - постоянные;

2)  ;

3)  .

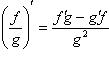
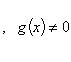Производная сложной функции

Если функции   имеют конечные производные   и  , то  . Значком внизу обозначена переменная, по которой вычисляется производная.

Таблица производных

Если x - независимая переменная, то справедливы формулы:

1)  ;

2) (a^x)' = a^x ln a,   a > 0,   (e^x)' = e^x;

3) (sin x)' = cos x;

4) (cos x)' = - sin x;

5)  ;

6)  ;

7)  ;

8)  ;

9)  ;

10)  ;

11)  ;

12) (sh x)' = ch x;

13) (ch x)' = sh x;

14)  ;

15)  ;

16)  ;

17)  ;

18)  ;

19)  .

пример

Вычислить производную функции y=(3x ³ -2x+1) sin x.

Решение. По правилу 3, y'=(3x ³ -2x+1)' sin x + (3x ³ -2x+1) (sin x)' =  = (9x ² -2)sin x + (3x ³ -2x+1)cos x.

7.Теоремы Ролля и Лагранжа

Теорема Ролля. Если функция f(x) непрерывна на замкнутом интервале [а, b], имеет внутри интервала производную и если

f(a) = f(b)

то внутри интервала [а, b] найдется хотя бы одно такое значение x₀ (a < x₀ < b), что

f ' (x₀) = 0.

Теорема Лагранжа. Если функция f(x) непрерывна на замкнутом интервале [а, b] и внутри него имеет производную f ' (x), то найдется хотя бы одно такое значение x₀ (a < x₀ < b), что

f(b) - f(a) = (b - a)f '(x).