Физический смысл производной.

Если  функция y = f(x) и ее аргумент x являются физическими величинами,  то производная   – скорость изменения переменной y относительно переменной x в точке .  Например, если S = S(t) – расстояние, проходимое точкой за время t,  то ее производная  – скорость в момент времени .  Если  q = q(t) – количество электричества, протекающее через поперечное сечение проводника в момент времени  t,  то   – скорость изменения количества электричества в момент времени , т.е. сила тока в момент времени .

 Геометрический смысл производной. Производная в точке x ₀ равна угловому коэффициенту касательной к графику функции y = f(x) в этой точке.

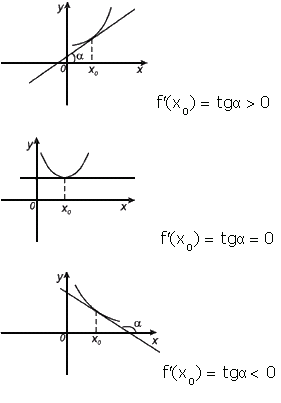
3.Определение касательной к графику функции

Определение. Пусть дана функция f, которая в некоторой точке x₀ имеет конечную производную f(x₀). Тогда прямая, проходящая через точку (x₀; f(x₀)), имеющая угловой коэффициент f ’(x₀), называется касательной.

Уравнение касательной

Пусть функция задается уравнением y=f(x), нужно написать уравнение касательной в точке x0. Из определения производной: 

y/(x)=limΔx→0ΔyΔx

Δy=f(x+Δx)−f(x). 

Уравнение касательной к графику функции: y=kx+b (k,b=const). Из геометрического смысла производной: f/(x0)=tgα=k Т.к. x0 и f(x0)∈  прямой, то уравнение касательной записывается в виде: y−f(x0)=f/(x0)(x−x0) , или

y=f/(x0)·x+f(x0)−f/(x0)·x0. 

 

 

Уравнение касательной

Всякая невертикальная прямая задается уравнением вида y = kx + b, где k — угловой коэффициент. Касательная — не исключение, и чтобы составить ее уравнение в некоторой точке x₀, достаточно знать значение функции и производной в этой точке.

Итак, пусть дана функция y = f(x), которая имеет производную y = f ’(x) на отрезке [a; b]. Тогда в любой точке x₀ ∈ (a; b) к графику этой функции можно провести касательную, которая задается уравнением:

y = f ’(x₀) · (x − x₀) + f(x₀)

Здесь f ’(x₀) — значение производной в точке x₀, а f(x₀) — значение самой функции.

Пример

Задача. Дана функция y = x³. Составить уравнение касательной к графику этой функции в точке x₀ = 2.

Решение. Уравнение касательной: y = f ’(x₀) · (x – x₀) + f(x₀). Точка x₀ = 2 нам дана, а вот значения f(x₀) и f ’(x₀) придется вычислять.

Для начала найдем значение функции. Тут все легко: f(x₀) = f(2) = 2³ = 8; Теперь найдем производную: f ’(x) = (x³)’ = 3x²; Подставляем в производную x₀ = 2: f ’(x₀) = f ’(2) = 3 · 2² = 12; Итого получаем: y = 12 · (x − 2) + 8 = 12x − 24 + 8 = 12x − 16. Это и есть уравнение касательной.

Ответ: y = 12x − 16

Задача. Составить уравнение касательной к графику функции f(x) = 2sin x + 5 в точке x₀ = π/2.

Решение. В этот раз не будем подробно расписывать каждое действие — укажем лишь ключевые шаги. Имеем: f(x₀) = f(π/2) = 2sin (π/2) + 5 = 2 + 5 = 7; f ’(x) = (2sin x + 5)’ = 2cos x; f ’(x₀) = f ’(π/2) = 2cos (π/2) = 0; Уравнение касательной: y = 0 · (x − π/2) + 7 = y = 7.

Ответ: y = 7

В последнем случае прямая оказалась горизонтальной, т.к. ее угловой коэффициент k = 0. Ничего страшного в этом нет — просто мы наткнулись на точку экстремума.

Уравнение касательной.

• Это прямая,значит ее уравнение

• y=kx+b

• k=tga= fi(x0)

• Y=fi(x0) x+b *

• точка касания А принадлежит графику. Значит ее координаты(x0.f(x0)) .обращают уравнение прямой в верное равенство

• f(x0)= fi(x0)х0+b

• отсюда b= f(x0)- fi(x0)х0

• y= fi(x0)х0+ f (x0)- fi(x0)х0

• y= f (x0)+ fi(x0) (х-х0)

Запомните! Y=f(x0)+f|(x 0)(x-x0)

Задачи на составление касательной к графику функции в точке ,принадлежащей графику

• Составьте уравнение касательной к графику функции f(x) = x2+3x+1в точке с абсциссой х0=1

• Решение.

• 1. х0 =1 -абсцисса точки касания.

• 2. Найдем f(1).f(1)=12+3*1+1=5

• 3. Найдем fi(x)и fi(x0), fi(x)=2х+3, fi(1)=5

• 4. Подставим найденные числа в общее уравнение касательной. y =f(x0)+ fi(x0) (x-x0), y = 5+5 (x-1), y = 5x+4

• Это и есть искомое уравнение касательной

Проведение касательной параллельной заданной прямой

• Задача1. Напишите уравнение всех касательных к графику функции y =x2-2x-8 параллельных прямой y= -4x-4

• Решение .1. Обозначим абсциссу точки касания х0

• 2.Найдем f(x0).f(x0)= x02-2x0-8

• 3.Найдем fi(x) и fi(x0). fi(x)=2x-2. fi(x0). =2x0-2

• Из условия параллельности следует,что fi(x0)= - 4, решив уравнение 2x0 -2 = - 4,

• получим х0 =-1.Подставим найденные значения в общее уравнение касательной y = f(x0)+ fi(x0) (x-x0), у= -5 - 4(х+1), у= - 4х-9 - уравнение касательной

4. Теорема о непрерывности дифференцируемой функции.

Непрерывность дифференцируемой функции

Теорема 1. Пусть функция y = f(x) дифференцируема на интервале (a, b). Тогда функция fнепрерывна на (a, b).