Вопросы к экзамену по курсу «Математика» для специальностей АС. III семестр.

1. функция нескольких переменных. Линии, поверхности уровня. Графическое изображение функции 2х переменных. Общее уравнение поверхности в пространстве. Простейшие поверхности 2го порядка. Цилиндрические поверхности.

1) Площадь прямоуг-ка S=ab это ф-я 2-х перемен. (2-х сторон) 2) Объём параллепип. V=xyz это ф-я 3-х переменных 3) f=x²+y²+z³+t⁴-s⁵

Рассмотрим к-то множество на двумерной плоскости множ-во точек М(x, y). Если каждой точке (x, y) из рассм. множ-во поставлено в соответствие некоторое число, то говорят, что на множ-ве задана ф-я. Z=f(x, y), (x, y) Є D Каждой паре (x, y) ставится в соответствие одно значение Z, (x, y)→z. Множ-во D назыв. областью определения.

Способы задания ф-ции: 1)аналитический (с пом. формулы) Z=f(x, y) 2) табличный 3) графический (обычно хорошо видны качественные св-ва – возраст., убывание, экстремумы)

Линии уровня. Поверх-ти уровня.1) z=f(x, y) Линией уровня ф-ии 2-х перем назыв. линия f(x, y)=C, изображ. на пл-ти xOy. Если линии уровня сужаются, то увеличив. крутизна поверхности. 2) u=φ(x, y, z). Для ф-ии 3-х переменных мы можем нарисовать область определения и поверхность уровня. Поверхность уровня созд. ур-ем: φ(x, y, z)=С. Общее уравнение поверхности в пространстве Ax+By+Cz+D=0

2. предел и непрерывность функции нескольких переменных.

z=f(x, y) Эпсилом (ε) – окрестностью в т.Z₀(x,y), назыв. множ-во во всех точках, для кот. Выполнено нер-во p(z, z₀)< ε (p – расстояние ) Число А, назыв. пределом ф-ии z=0 A(x,y), при стремлении т. М(x,y), если для любого «+» ε найдётся такое «+» δ, что для всех т. М(х,y), для кот. выполнено нер-во p(M, M₀)< δ, следует выполнить нер-во f(x, y)-A< δ A=lim f(x, y); M→M₀; x→x₀; y→y₀;

Непрер-сть ф-ии 2-х перемен. Ф-я z=f(x,y) назыв. непрер. в т. М₀(x₀,y₀), если в этой точке сущ. предел, причём он конечен и совпадает со знач. ф-ции. Ф-я z=f(x,y) – назыв. непрерывной в т.М₀(x₀,y₀), если бесконечно малым приращ. аргумента ∆х, ∆y соотв. бесконечно малое приращ-е ф-ии ∆z.

3. Дифференцируемые функции. Дифференциалы. Частные производные. Необходимое и достаточное условие дифференцируемости.

Дифференц-е сложных ф-ци ; ;

1) z=f(x,y), x=x(t), y=y(t), t – независим. перемен.

2) z=f(x,y), y=y(x), x – независим. перемен. – полная произв.

3) z=f(x,y), x=x(u,v), y=y(u,v), u,v – независим. перемен.

Дифференцирование неявных ф-ций

1) x²+y²=4 Дифференцируем лев. и прав. часть, учитывая, что y=y(x). 2x+2yy'=0 ; пусть задана неявная ф-я одной переменной F(x,y)=0. Если ф-я =0, то её диф-л =0, т.е dF=0,

2) Пусть задана неявная ф-я 2-х перемен. F(x,y,z)=0; ;

Частные и полные дифф-лы

dy=y'dx Частным диф-лом ф-ии z=

=f(x,y) назыв. прпоизведение соотв. частной произв. на приращ-е соотв. аргумента.

Полным диф-лом ф-ии назыв. сумма частных диф-лов.

Диф-л ф-ции 2-х перемен. зависит от 4-х переменных x, y, dx, dy. При малых dx, dy полное приращ-е ф-ии ≈ полному диф-лу:

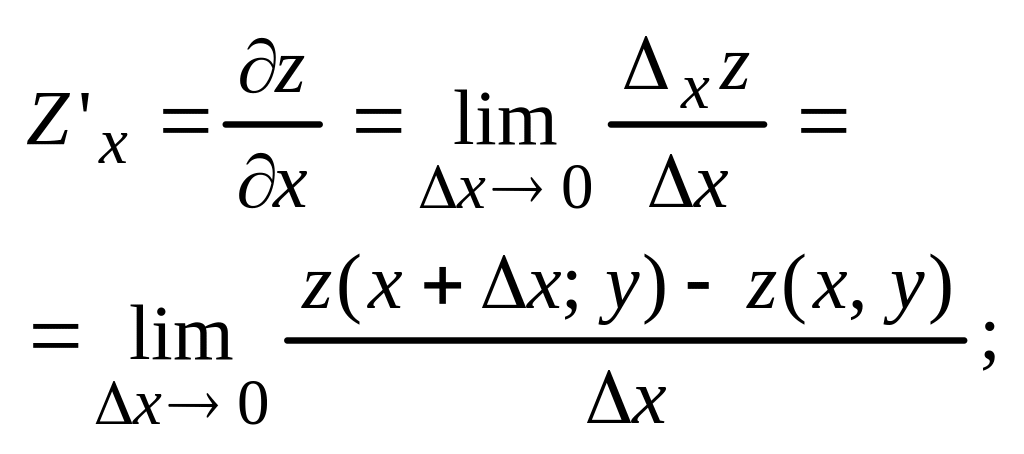
Частные производные Z=f(x,y) – частными приращ. по x или по y, наз. приращ. ф-ии при услов., что др. аргумент фиксирован ∆_хZ=Z(x+∆x; y)-Z(x, y); ∆_yZ=Z(x, y+∆y)-Z(x,y) Частной производной по перемен. x (по y), назыв. предел отношения частного приращ-я ф-ии к приращ. аргумента. 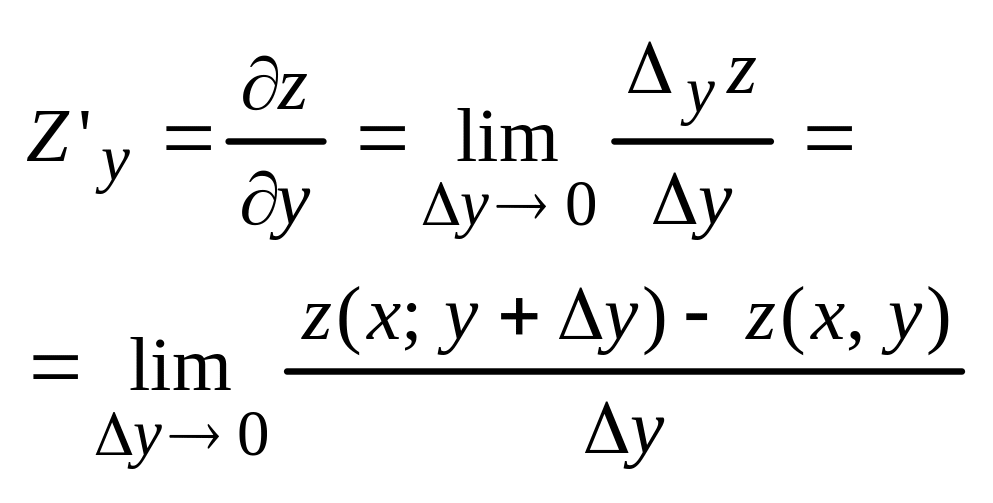При вычислении производной Ox считается постоянным y. При вычислении произв. Oy считается постоян. x. Если ф-я большего числа переменных рассм., то постоян. считаются все перемен. кроме той, по кот. берётся производная.

4. уравнение касательной к плоскости и нормали к поверхности. Геометрический смысл дифференциала.

Касательная пл-ть и нормаль

1) Рассм. пересеч-е поверхности z=f(x,y) пл-тью y=y₀; пересеч-ем явл. некотор. линия. К этой линии в этой пл-ти проводим касат. прямую.

2) Рассм. пересеч-е поверхности пл-тью x=x₀. К получен. линии в этой пл-ти проводится касат. прямая.

3) Ч/з 2 пересек. касат. прямых проводится пл-ть. Эта пл-ть назыв. касат пл-тью к поверхности z=f(x,y) в т.М₀

Если поверхность задана явно, то ур-е касат. пл-ти имеет вид:

Нормалью к поверхности Z=f(x,y) назыв. нормаль её касат. пл-ти. Пусть поверхность задана в неявном виде F(x,y,z)=0 M₀(x₀,y₀,z₀). Ур-е касательной: Ур-е нормали:

5. производная по направлению. Связь с частными производными. Геометрический и физический смысл.

Производная по направлению

Рассмотрим область в 3-х мерном пространстве. Пусть в каждой точке (из области D) определена скалярная ф-я в этом случае говорят, что на области D задано скалярное поле. Поверхностью уровня скалярного поля наз. геом. место точек, для кот. выполнено условие: Для скалярного поля в 3-х мерной области мы можем нарисовать только поверхность уровня. Поверхностями уровня явл. всевозм. сферы с центром в начале коорд-т. Из т. P берём произвольный луч. Обозначаем единичный вектор, соответств. данному направлению. P₀(x₀,y₀,z₀) углы м/у вектором и осями Ox, Oy, Oz. На луче рассм. произв. точку P(x,y,z) Ур-е сферы имеет вид: Производной по направлению в т.P₀ наз. предел p=|PP₀| – расстояние РР₀ u'_λ – u' по направлению λ Произв. по направлению вычисл. по след. формуле: cosα, cosβ, cosγ – направляющие cos вектора λ.

6. градиент и его свойства. Метод наискорейшего спуска.

Градиенты 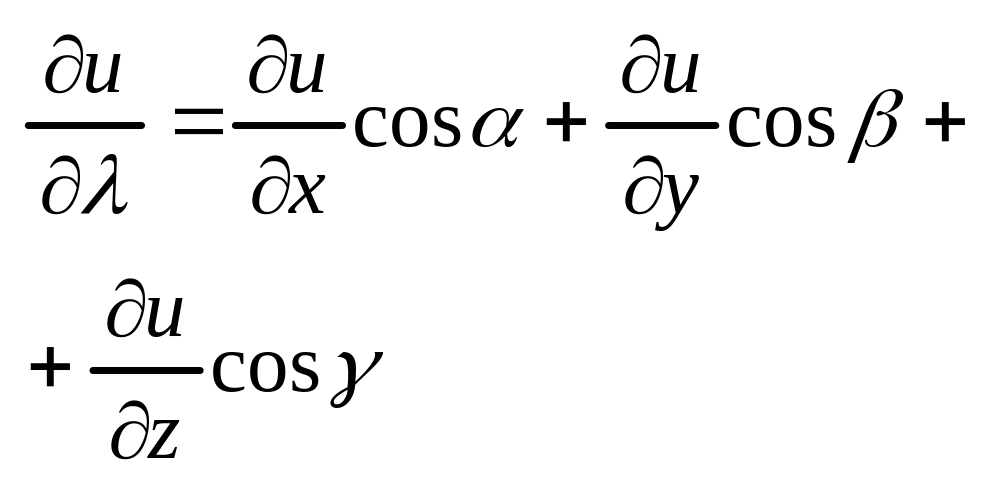=(cosα, cosβ, cosγ). Градиентом (grad u) скалярного поля наз. вектор, составлен. из частных производных. будет max, если cosφ=1, φ=0.

Производная по направлению max, если это направление совпадает с grad u

Производная по направлению min, если cosφ=-1, φ=π. Произв. миним. в направлении, противоположном направлению градиента, это напр. назыв. антиградиент (-grad u).

7. частные производные, дифференциалы высших порядков. Теорема о смешанных производных. формула Тейлора функции нескольких переменных. примеры.