Практическая работа №11
Тема: Итерационные циклы. Решение нелинейных уравнений.
Практическая работа №12
Тема: Вычисление пределов. Нахождение корня вида y=
Содержание отчета
1. Четко сформулированное условие задачи (постановка задачи, исходные данные, ожидаемый результат).
2. Математическое описание задачи (формулы, преобразование, графики).
3. Контрольный счет
4. Схема алгоритма (в исключительных случаях – словесное описание).
5. Описание переменных.
6. Текст программы (простой и модифицированной с заголовком программы и минимальными комментариями).
7. Результат работы программы (результаты обязательно должны быть на одном листе с модифицированной программой).
8. Вывод.
Практические работы
Практическая работа №1
Тема: Работа со встроенными функциями языка Turbo Pascal.
Цель: Составление и отладка программ для вычисления функций и контроля их работ.
Задание: Рассмотреть работу функций языка Turbo Pascal: DIV, MOD, ODD, INT, CHR, SUCC, PRED, TRUNC, ROUND, RANDOMIZE.
Практическая работа №2
Тема: Оператор варианта CASE.
Цель: Составление, редактирования и отладка программ с оператором выбора CASE.
Задание: Индивидуальное задание.
В1.
Составить программу вычисления площадей различных фигур.
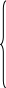a*b,
если n=1;
,
если n=2;
S=
,
если n=3;
,
если n=4;
,
если n=5;
В2.
Составить программу вычисления площадей различных фигур:
P*1, если k=1;
,
если k=2;
S=
,
если k=3;
,
если k=4;
,
если k=5;
,
если k=6;
В3.
Найти
остаток от деления целой части значения
функции Z
= ln(
+ab)на
7 и в зависимости от его величины
напечатать сообщение об одном из дней
недели пронумеровав их от 0 до 6.
В4.
Используя оператор выбора вычислить значение функции.
a
+ bx + c
,
если
1
<2;
(a
sin (x*b))
,
если
2
<3;
S=
+c,
если
3
<4;
a*ln(
),если
4
<5;
,
если 5
<6;
В5.
Даны
три целых положительных числа a,
b,
c.
Определив остаток К, от деления на 3
величины М, равной М=
,
вычислить значение функции.
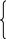e
^ (m+c), при
k=0;
Y = ln (a/b), при k=1;
,
при k=2.
В6.
Используя оператор выбора вычислить значение функции.
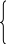1-sin
(x),
при 5
<10;
(1+cos(x)),
при 10
<15;
Y= 1/3(tg(x)), при 15 <20;
ctg
(x),
при 20
<25;
В7.
Даны три целых положительных числа a, b, c. Определив остаток К, от деления на 3 величины М, равной М= , вычислить значение функции.
,
при k=0;
Y
=
,
при k=1;
,
при k=2;
В8.
Составить программу вычисления объемов различных фигур.
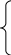s*h,
при
n = 1;
a*b*c, при n = 2;
V = 1/3s*h, при n = 3;
,
при n
= 4;
4/3
,
при n
= 5.
В9.
Используя оператор выбора вычислить значение функции.
,
при a
= -1;
Z
=
,
при a
= 0;
,
при a
= 1;
,
во всех остальных случаях.
где а-целое число и -1<a<3
В10.
Ввести время суток и вывести соответствующее ему действие на русском языке.
В11.
«Вечный календарь». Даны натуральные числа a, b, c, которые обозначают число, месяц и год. Определить день недели, на который недели падает указанная дата.
При решение этой задачи можно считать, что исследуемая дата лежит в диапазоне от 1582 до 4902 гг. В этом случае номер дня недели (воскресенье имеет номер 0, понедельник-1, суббота-номер 6) равен остатку от деления на 7 от значения выражения.
(2,6m-0,2)+d+y+(y/4)+(c/4)-2c, где
d-номер дня в месяц (1,2,…);
m-номер месяц в году, нумерация начинается с марта (март имеет номер 1, апрель номер 2,…, декабарь-номер 10, январь и февраль считаются месяцами с номерами 11 и 12 предыдущего года).
y-две младшие цифры года (00,…,99);
c-две старшие цифры года (15,…,49);
(x)-означает целую часть числа x.