17. Магнитный и механический моменты электронов. Спин. Опыты Штерна и Герлаха.
Спин
– собственный момент импульса
элементарных частиц, имеющий квантовую
природу и не связанный с перемещением
частицы как целого. Несмотря на то, что
спин не связан с реальным вращением
частицы, он тем не менее порождает
определённый магнитный момент.
Механический момент электрона:
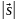=Ms=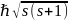
,
где s=1/2
– спиновое квантовое число. Спин частицы
может быть целым или полуцелым. Опыт
Штерна и Герлаха: В
1922 данный опыт экспериментально
подтвердил, что атомы обладают магнитным
моментом, проекция которого на направление
внешнего магнитного поля принимает
лишь определённые значения (пространственно
квантована). Штерн и Герлах исследовали
прохождение пучка атомов серебра(а
затем и др. элементов) в сильно неоднородном
магнитном поле с целью проверки
теоретически полученной формулы
пространств. квантования проекции mz
на направление Z магнитного момента
атома m₀: mz=m₀m (т = 0±1,...). На атом, обладающий
магнитным моментом и движущийся в
неоднородном вдоль Z магнитном поле Н,
действует сила F= mz ∂Н/∂Z, которая
отклоняет его от первоначального
направления движения. Если проекция
магнитного момента атома могла бы
изменяться непрерывно, то на пластинке
наблюдалась бы размытая широкая полоса.
Однако в опыте было обнаружено расщепление
пучка атомов на 2 компоненты, симметрично
смещенные относительно первичного
направления распространения на величину
D — на пластинке появлялись две узкие
полосы. Это указывало на то, что проекция
магнитного момента атома mz на направление
поля Н принимает только два отличающиеся
знаком значения ±m₀, т. е. m₀ ориентируется
вдоль Н и в противоположном направлении.
18.Результирующий механический момент многоэлектронного атома. J-j и l-s связь.
При сложении моментов отдельных электронов в результирующий момент атома возможны два случая.
1. Орбитальный и спиновой моменты каждого электрона складываются в результирующий момент, которые уже затем объединяются в суммарный момент атома. Такой вид связи называется j-j связью. Обычно такая связь наблюдается у тяжелых атомов.
2. Наиболее часто встречающаяся у атомов L-s связь (связь Рассел - Саундерса) осуществляется по следующей схеме:
а)
Все орбитальные механические моменты
отдельных электронов складываются в
орбитальный момент, величина которого
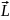определяется квантовым числом L
суммарного орбитального момента атома.
Число всегда является целым числом
либо нулем.
б)
Спиновые моменты импульса всех электронов
многоэлектронного атома складываются
в суммарный спиновой момент
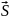При этом в атомах с четным числом
электронов квантовое число S
принимает все целые значения от нуля,
когда спины электронов попарно
компенсируют друг друга, до целого
значения N/2,
когда спины всех электронов направлены
в одну сторону. При нечетном квантовое
число может принимать все полуцелые
значения от 1/2 до N/2.
в)
Результирующий момент всего атома
есть результат квантовомеханического
сложения моментов
и
,
которое сводится к правилу сложения
квантовых чисел L
и S.
Все возможные значения результирующего
механического момента атома определяются
формулой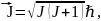
в
которой квантовое число имеет одно из
следующих значений: от |L-S|
до L+S.
У атомов с четным числом электронов число J целое, а у атомов с нечетным числом электронов - полуцелое.
L,S,J
– квантовые числа суммарных орбитальных,
спиновых и полных механических моментов
электронов атома соответственно. j-j:
,
,
.
,
,
.
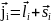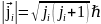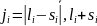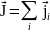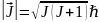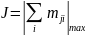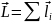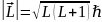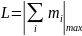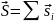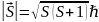L-S:
,
,
;
,
,
S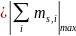
;
,
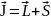