7. Опыты Резерфорда по рассеянию α- частиц. Формула Резерфорда. Модель атома Резерфорда-Бора.

Изучение прохождения α- частиц через тонкие пластинки металлов. α- частицы испускаются источником 1, помещенным внутри свинцовой полости с каналом 2. Все α- частицы, кроме движущихся вдоль канала, поглощались свинцом. Узкий пучок α- частиц попадал на фольгу из золота 3 перпендикулярно к ее поверхности; α- частицы, прошедшие сквозь фольгу и рассеянные ею, вызывали вспышки на экране 4. Опыты Резерфорда показали, что почти все α- частицы, прошедшие сквозь фольгу, сохраняли прежнее направление своего движения или отклонялись на малые углы. Лишь некоторые α- частицы отклонялись на большие углы 135-150. Формула Резерфорда: 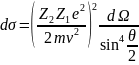dσ – дифференциальное сечение, θ – угол рассеяния. Ядерная модель атома – модель структуры атома, в которой весь положительный заряд атома считается сосредоточенным в ядре – в облати занимающей малый объем по сравнению со всем объемом атома.

8.Закономерности в спектрах атома водорода. Серии Лаймана, Бальмера, Пшена. Комбинационный принцип Ритца

Спектр излучения атома водорода является линейчатым. В 1890 году И. Ридберг получил эмпирическую формулу для частот спектральных линий: 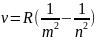.Для серии Бальмера(видимая) m = 2, n = 3, 4, 5,…; Серия Лаймана (УФ) m=1, n=2,3…; Серия Пашена (ИК) m=3,n=4,5… Комбинационный принцип Ритца: =Т_m –T_n; волновое число любой спектральной линии может быть представлено как комбинация двух термов.

9. Дискретность квантовых состояний атома. Постулаты Бора. Опыты Франка-Герца.

Первый постулат Бора (постулат стационарных состояний): в атоме существуют некоторые стационарные состояния, не изменяющиеся во времени без внешних воздействий. В этих состояниях атом не излучает электромагнитных волн.Второй постулат Бора (правило частот): при переходе атома из одного стационарного состояния в другое им испускается или поглощается один квант энергии. hν=En-Em. Опыты Франка – Герца: опыты, в которых исследовалась вольтамперная характеристика I=f(U) наполненной парами ртути трех электродной лампы и было обнаружено, что на кривой I=f(U) имеется ряд острых максимумов, отстоящих друг от друга на расстоянии 4,9 В и отделенных друг от друга глубокими минимумами, которые обусловлены неупругими столкновениями электронов с атомами.

10. Спонтанные и вынужденные переходы. Коэффициенты Эйнштейна. Спектральная плотность излучения.

Вероятности спонтанных и вынужденных переходов между m-м и n –м уровнями: P_сп = Z_сп/N_n = A_nm; P_вын = Z_вын/N_n = В_nmρ_v; P=Z/N_m=B_mnρ_v, где Z – число переходов в единицу времени, N_n N_m – населенности m-го и n-го уровней, ρ_v – объемная спектральная плотность внешнего излучения частоты ν, под действием которого совершаются вынужденные переходы; A_nmВ_nmB_mn – коэффициенты Эйнштейна. значения коэффициентов Эйнштейна пропорциональны квадратам матричных элементов: R_mn=ψ_mpψ_ndV. Связь между коэффициентами Эйнштейна: В_nm = g_m/g_n ·B_mn= 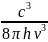A_nm. Спектральная плотность излучения — характеристика спектра излучения, равная отношению интенсивности (плотности потока) излучения в узком частотном интервале к величине этого интервала. Является применением понятия спектральной плотности мощности к электромагнитному излучению.