
- •2.Принцип относительности Галилея. Преобразования Галилея.
- •4. Теоремы об изменении импульса и момента импульса.
- •5.Свойства потенциальных полей
- •6.Теорема об изменении кинетической энергии материальной точки.
- •7.Теорема об изменении импульса механ. Системы.
- •8. Выделение движения центра масс и относительного движения механической системы.
- •9. Теорема об изменении момента импульса механической системы.
- •3. Законы Ньютона. Методы решения задач в мех Ньютона.
- •10. Теорема об изменении кинетической энергии механической системы.
- •17. Общее ур-е механики.
- •18. Решение задачи о движении тела по наклонной плоскости в поле сил тяжести на основании ур-я Лагранжа 1го рода.
- •21.Вариационный принцип.
- •22.На основании ур-я Лагранжа-Эйлера получить ур-я колебаний метем.Маятника и колеб. Точки под упругой силы.
- •27. Решение задачи Кеплера в формализме Лагранжа.
- •28. Законы Кеплера.
- •41. Законы сохранения физических величин в формализме Гамильтона
- •42. Фазовое пространство. Закон сохранения потока точек фазового пространства
- •41. Движение заряженной частицы в электромагнитном поле в формализме Лагранжа
- •42. Движение заряженной частицы в электромагнитном поле в формализме Гамильтона
- •51. Уравнение Эйлера для вращения твердого тела.
- •52. Решение уравнения Эйлера для вращения твердого тела.
- •49. Момент импульса вращения твердого тела.
- •58.Кинем. Перем-е рел.Мех-ки
- •48. Определение кин энергии вращающегося твердого тела
- •57.Преобразования Лоренца.
- •56.Качественный анализ уравнения вращения твёрдого тела в поле сил тяжести.
- •19.Решение задачи о движении двух тел на нерастяжимой нити, перекинутой через блок, на основании общего уравнения механики.
- •11.Описание мат.Маятника на основании 2 –го закона Ньютона и зак сохр эн
- •20.Анализ примера о движении тела, брошенного под углом в поле сил тяжести, методом вариации функции действия.
- •44.Каноническое преобразование
27. Решение задачи Кеплера в формализме Лагранжа.
![]()
Кинетическая энергия в центрально-симметричном поле:
![]()
Потенциальная энергия:
![]()
M-масса солнца, m-масса планеты.
В этом случае система имеет 2 степени свободы:
![]()
Уравнения Лагранжа-Эйлера будут:
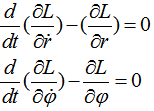
![]()
![]()
![]()
![]()
тогда:
![]()
![]()
Т. к.
![]()
то
уравнение Лагранжа-Эйлера явно не
зависит от![]() ,
то
- циклическая величина.
,
то
- циклическая величина.
![]()
Пусть
![]()
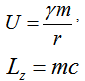
Перепишем (1) с учетом введенных констант:
![]()
![]()
![]()
r=r(φ)
Каким расст. от силового центра в зав. от φ:
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
Общее решение:
![]()
28. Законы Кеплера.
Законы Кеплера — три эмпирических соотношения, интуитивно подобранных на основе анализа астрономических наблюдений
Первый
закон Кеплера (закон эллипсов).Каждая
планета Солнечной
системы
обращается по эллипсу,
в одном из фокусов которого находится
Солнце.Форма
эллипса и степень его сходства с
окружностью характеризуется отношением
![]() ,
где c
— расстояние от центра эллипса до его
фокуса (половина межфокусного расстояния),
a
— большая полуось. Величина e
называется эксцентриситетом
эллипса. При c
= 0 и e
= 0 эллипс превращается в окружность.
Второй
закон Кеплера (закон площадей).Каждая
планета движется в плоскости, проходящей
через центр Солнца, причём за равные
времена радиус-вектор, соединяющий
Солнце и планету, описывает равные
площади.
Третий
закон Кеплера (гармонический закон)Квадраты
периодов обращения планет вокруг Солнца
относятся, как кубы больших полуосей
орбит планет. Справедливо не только
для планет, но и для их спутников.
,
где c
— расстояние от центра эллипса до его
фокуса (половина межфокусного расстояния),
a
— большая полуось. Величина e
называется эксцентриситетом
эллипса. При c
= 0 и e
= 0 эллипс превращается в окружность.
Второй
закон Кеплера (закон площадей).Каждая
планета движется в плоскости, проходящей
через центр Солнца, причём за равные
времена радиус-вектор, соединяющий
Солнце и планету, описывает равные
площади.
Третий
закон Кеплера (гармонический закон)Квадраты
периодов обращения планет вокруг Солнца
относятся, как кубы больших полуосей
орбит планет. Справедливо не только
для планет, но и для их спутников.![]() ,
где T1
и T2 —
периоды обращения двух планет вокруг
Солнца, а a1
и a2 —
длины больших полуосей их орбит.Ньютон
установил, что гравитационное
притяжение
планеты определенной массы зависит
только от расстояния до неё, а не от
других свойств, таких, как состав или
температура. Он показал также, что
третий закон Кеплера не совсем точен —
в действительности в него входит и
масса планеты:
,
где T1
и T2 —
периоды обращения двух планет вокруг
Солнца, а a1
и a2 —
длины больших полуосей их орбит.Ньютон
установил, что гравитационное
притяжение
планеты определенной массы зависит
только от расстояния до неё, а не от
других свойств, таких, как состав или
температура. Он показал также, что
третий закон Кеплера не совсем точен —
в действительности в него входит и
масса планеты:
![]() ,
где M —
масса Солнца, а m1
и m2 —
массы планет.
,
где M —
масса Солнца, а m1
и m2 —
массы планет.
29. Основные элементы описания линейных многомерных колебаний в формализме Лагранжа.
Введем многомерный вектор:
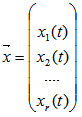
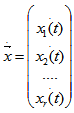
При введении многомерных векторов и матриц уравнение функции Лагранжа для колеблющейся многомерной системы в линейном приближении можем переписать в виде:
![]()
42. Фазовое пространство. Закон сохранения потока точек фазового пространства
Фазовое пространство это множество точек которые задается с помощью осей на которых откладываются обобщенныекоордин.

Распр. т. фазового пространства определённая физическая величина не изменяется т.е. пост.
30.УРАВНЕНИЯ КОЛЕБАНИЙ МНОГОМЕРНОЙ СИСТЕМЫ В ФОРМАЛИЗМЕ ЛАГРАНЖА В ЛИНЕЙНОМ ПРИБЛИЖЕНИИ.
Запишем уравнение в виде Лагранжа-Эйлера:

В дальнейшем будем рассматривать мех.сист. у которых матрицы m и æ являются симметричными.

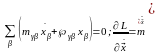
 ;
;


31 ОПРЕДЕЛЕНИЕ СОБСТВЕННЫХ ЧАСТОТ МНОГОМЕРН.КОЛЕБ В ЛИН.ПРИБЛЕЖЕНИИ.
Будем рассматривать р-е ур-ийдв-я кол-ся мех-ой сис-мы в линприбл.,т.е когда будем строить ф-ю Лагранжа, то ф-ии будет реализовывать разложение слагаемых до 2ого порядка по оклон. обобщающих координ. от состояния устойчивого равновесия
 L(ϕ,ψ,ϕ,ψ)Пусть
механич. сис-ма имеет r
степеней свободы. Эта механич.
cис-маопредел-сяобобщ
.коорд. коорд-ми q1,q2….qr..Обозначим
qr,где
L=1,2….r,тогда
L=L(qλ,qλ)=T-U(qλ)
L(ϕ,ψ,ϕ,ψ)Пусть
механич. сис-ма имеет r
степеней свободы. Эта механич.
cис-маопредел-сяобобщ
.коорд. коорд-ми q1,q2….qr..Обозначим
qr,где
L=1,2….r,тогда
L=L(qλ,qλ)=T-U(qλ)
Будем
рассматривать состо-я мех сис-мы,гдепотенц.
энергия минимальна.Xλ=qλ-q(0)λ
отклон.
обобщ. коорд-тыот положения
равновесия.U(qλ)=U(q(0)λ+xλ)=
U(q(0)λ)+ +
+
 +….
+….
T= Ф-ю Лагранжа для колеб. многомерной
сис-мы в лин.приближении можем записать
в виде L=
Ф-ю Лагранжа для колеб. многомерной
сис-мы в лин.приближении можем записать
в виде L= где
где
 координаты опред.пар-ми
координаты опред.пар-ми
 коэ-ты
коэ-ты
