
- •2.Принцип относительности Галилея. Преобразования Галилея.
- •4. Теоремы об изменении импульса и момента импульса.
- •5.Свойства потенциальных полей
- •6.Теорема об изменении кинетической энергии материальной точки.
- •7.Теорема об изменении импульса механ. Системы.
- •8. Выделение движения центра масс и относительного движения механической системы.
- •9. Теорема об изменении момента импульса механической системы.
- •3. Законы Ньютона. Методы решения задач в мех Ньютона.
- •10. Теорема об изменении кинетической энергии механической системы.
- •17. Общее ур-е механики.
- •18. Решение задачи о движении тела по наклонной плоскости в поле сил тяжести на основании ур-я Лагранжа 1го рода.
- •21.Вариационный принцип.
- •22.На основании ур-я Лагранжа-Эйлера получить ур-я колебаний метем.Маятника и колеб. Точки под упругой силы.
- •27. Решение задачи Кеплера в формализме Лагранжа.
- •28. Законы Кеплера.
- •41. Законы сохранения физических величин в формализме Гамильтона
- •42. Фазовое пространство. Закон сохранения потока точек фазового пространства
- •41. Движение заряженной частицы в электромагнитном поле в формализме Лагранжа
- •42. Движение заряженной частицы в электромагнитном поле в формализме Гамильтона
- •51. Уравнение Эйлера для вращения твердого тела.
- •52. Решение уравнения Эйлера для вращения твердого тела.
- •49. Момент импульса вращения твердого тела.
- •58.Кинем. Перем-е рел.Мех-ки
- •48. Определение кин энергии вращающегося твердого тела
- •57.Преобразования Лоренца.
- •56.Качественный анализ уравнения вращения твёрдого тела в поле сил тяжести.
- •19.Решение задачи о движении двух тел на нерастяжимой нити, перекинутой через блок, на основании общего уравнения механики.
- •11.Описание мат.Маятника на основании 2 –го закона Ньютона и зак сохр эн
- •20.Анализ примера о движении тела, брошенного под углом в поле сил тяжести, методом вариации функции действия.
- •44.Каноническое преобразование
17. Общее ур-е механики.
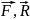
реакция связи, наз.идеальной для одной матер.точки,есливыполн.ур-е:
(

Принцип Д*аламбера:
При
движ-ииматер.точки сил
действующих на матер.точку =0
сил
действующих на матер.точку =0
 =
-m
=
-m

Если
ур-е (7.9) скалярно умножим на
,
то ( =0
(7.10), это ур-е наз.общимур-ем механики
для одной матер.точки.
=0
(7.10), это ур-е наз.общимур-ем механики
для одной матер.точки.
Для сис-мы состоящ.изnматер.точек принцип Д*аламбера будет записан так:
 n=1,2…
n=1,2…
Если умножим (7.11) скалярно на , а затем проссумируем.то получим:
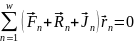
Если связь идеальна, то это ур-е запиш. В виде:

Общее ур-е механики
18. Решение задачи о движении тела по наклонной плоскости в поле сил тяжести на основании ур-я Лагранжа 1го рода.
m
=
m
 =
=
 f(
f(
x=
 cos;
h-y=
sihn;
y=ax+b; y=ax+h; b=h
cos;
h-y=
sihn;
y=ax+b; y=ax+h; b=h
a ;
a=-
;
a=-
ур-ереакциисвязи:
y+tgx-h=0;
f= y+tgx-h;
 ;=mgco
;=mgco ;
;
 ;
;
 ;
m
;
m =
= ;
;
 =-mg+;
y= -xtg+h
=-mg+;
y= -xtg+h
(-tg)
=
 =
-
=
-
 =
-g+
=
-g+ ;
=
-
;
-
=
-g+
;
=
-
;
-
=
-g+
g=
 )=
)=
= ;
x=
;
x= ;
;
 =
-
=
- ;
;
y=
- ;
;
 ;
;
 ;
y=
;
y=
21.Вариационный принцип.
Урав. Лагранжа-Эйлера
Пример:
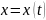
 – ф-я
– ф-я
действия.


Где
 будет
малая величина . При дальнейших
вычислениях будем ограничиваться 1-м
порядком малости по
.
будет
малая величина . При дальнейших
вычислениях будем ограничиваться 1-м
порядком малости по
.
 .
.



Ф-я действия будет
min,если

Поскольку пределы интегрирования по времени выбраны произвольным образом, то этот интеграл =0,если подинтеграл. выраж. =0. Поскольку отлично от 0, то выраж.в квадратной скобке=0.

Каждой степени
свободы ставиться в соответствие
независящая обобщённая координата. В
общем случае обобщ. Корд.мех. сист.
 все
rобобщ.
коорд. независимы друг от друга.
Соответственно обобщ. скорости
все
rобобщ.
коорд. независимы друг от друга.
Соответственно обобщ. скорости
 они также независимы друг от друга.
они также независимы друг от друга.
Ф-я Лагранжа(L) назыв. разность T-U, где T-кинитич. энергия, U-потенц. энерг. системы.
L= T-U
T=T ( ,
,

U=U
( ,
то ф-я Лагранжа
будет ф-я обобщ.коорд. и скоростей.
,
то ф-я Лагранжа
будет ф-я обобщ.коорд. и скоростей.
L=L(
Ур-я Лагранжа-Эйлера.
Ф-яЛагр. Для мех.
сист.с одной степенью свободы будет:
L=T-U=L(q,

Для получения ур-я движ. мех.сист. 1-й степени свободы воспользуемся принципом наименьшего действия (вариационный принцип).
 (поскольку
операция варьирования и дефференц.по
времени, а следоват.иинтегриров. по
времени перестановочные операции, то
операц. варьирования поднесём под
(поскольку
операция варьирования и дефференц.по
времени, а следоват.иинтегриров. по
времени перестановочные операции, то
операц. варьирования поднесём под
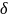 ,
тогда)=
,
тогда)=


Ур-я Лагранжа-Эйлера, движущ-ся точки в центрально симметр.поле:



23.Уравнение
Лагранжа -Эйлера для системы с многими
степенями свободы.
Пусть
мех.сис-маопр-сякоор-ми q1,q2..qr,где
r-число
степеней свободы {qα},α=1,2..r.Обоб.
скорости { .Тогда
ф.Лагранжа для мех. сис. с r
степ. свободы L=L{qα,
.Тогда
ф.Лагранжа для мех. сис. с r
степ. свободы L=L{qα, С помощью прин-ципа наименьшего принципа
найдём уравнение движения S=
С помощью прин-ципа наименьшего принципа
найдём уравнение движения S= δS=0
δS=
δS=0
δS= =
= +
+ =
=
Δqαdt=0 В рез.пол.

22.На основании ур-я Лагранжа-Эйлера получить ур-я колебаний метем.Маятника и колеб. Точки под упругой силы.
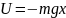

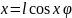


Ур-е связи.



Ур-е Лагранжа

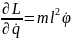


Лагранжев формализм:

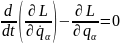

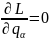

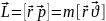

24.Обобщенные
координаты, скорости и импульса.
Циклические координаты. Законы сохранения
обобщенных импульсов.
В
формализме Лагранжа обоб.имп. мех. сис.
Пα=
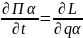
Опр. Цикл.коор-т
Обоб.коор-ты qβназ.цикл.,если ф-ия Лагранжа явно не зависит от этих корт,т.е
 ,тогда
каждой цикл.коор-те соот-ет сохр-ся
обоб.импульс
,тогда
каждой цикл.коор-те соот-ет сохр-ся
обоб.импульс
 (вып.закон
сохр.обоб.импульсов)
(вып.закон
сохр.обоб.импульсов)
25.0писание
движения материальной точки в
потенциальном сферическисимметричном
поле в полярных координатах в формализме
Лагранжа.
L= -U(r)В
данном случае мат.точка имеет 2
степ.свободы,этим степ. Свободы соот.
2 обоб.коор-ты r,
и 2 обоб. скорости
-U(r)В
данном случае мат.точка имеет 2
степ.свободы,этим степ. Свободы соот.
2 обоб.коор-ты r,
и 2 обоб. скорости
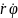 =>
движ.мат.точки будет опр-ся 2 обоб. имп.
Пr=
=>
движ.мат.точки будет опр-ся 2 обоб. имп.
Пr=
 Пφ=
Пφ= Ф. Лагранжа не зав. от φ
Ф. Лагранжа не зав. от φ
Пφ= -момент
импулься точки дви-ся в пл.орбиты.
-момент
импулься точки дви-ся в пл.орбиты.
26.
Функция Гамильтона. Привести примеры
на определение функции Гамильтона.
 Пα=
-обоб.импульс.
Опр-м энергию мех.сис-мы.Если мех.сис-ма
опр-ся ур-ем Лагранжа,кот.я вно не зав.
от времени,то говорят,что мех
сис.стационарна,а если явно зав.то не
стационарна,т.е.
Пα=
-обоб.импульс.
Опр-м энергию мех.сис-мы.Если мех.сис-ма
опр-ся ур-ем Лагранжа,кот.я вно не зав.
от времени,то говорят,что мех
сис.стационарна,а если явно зав.то не
стационарна,т.е.
R(qα, α,t)
α,t)
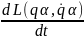 =
=

+ =
= +
+
(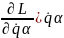 +
=
+
=
+ α
α- L(qα, α,t)]=- Из ур.следует,что если мех.сис-ма стац-на,то
 и
вел. H(qα,
и
вел. H(qα,
= α-L
явл. Сохр-ся вел.т.е явл. Инте-ом движения.
α-L
явл. Сохр-ся вел.т.е явл. Инте-ом движения.
И это есть ф.Гамильтона
Физ.смысл:
Расс.движ. точки в центр-ом поле
L=T-U= x,y,z-обоб.коор-ты
L(x,y,z+
x,y,z-обоб.коор-ты
L(x,y,z+ явно
от времени не зав.
явно
от времени не зав.

H=Пх +Пу
+Пz
+Пу
+Пz
- или H=
или H= +
U(r)Пример:Движ.мат.
точки с сфер.-сим. Поле в полярной СК
+
U(r)Пример:Движ.мат.
точки с сфер.-сим. Поле в полярной СК
L(r,φ, =
= (
( -U(r)
-U(r)
Пr=
Пφ= -обоб.импульс

H(r,
φ, +U(r)=
+U(r)= =H
=H
