Тема 5 Математические модели каналов связи. Преобразование сигналов в каналах связи

Лекция 5.1 Прохождение сигналов через каналы связи

5.1.1 Прохождение случайных сигналов через детерминированные линейные и нелинейные системы

Исследование преобразований случайных сигналов при их прохождении через динамические системы связано с решением задач двух типов:

- определение ФК (или СПМ) отклика y(t) на выходе системы, заданной своими характеристиками, по данной ФК (или СПМ) входного воздействия x(t);

- определение многомерного распределения вероятностей отклика y(t) на выходе системы по многомерному распределению входного воздействия x(t).

Вторая из указанных задач является более общей. Из её решения может быть получено решение первой задачи.

5.1.1.1 Прохождение случайных сигналов через линейные каналы

Линейный стационарный канал является неискажающим (не меняет форму входного сигнала), если его ИХ равна:

где γ – масштабный коэффициент; t₀ – постоянная задержка в канале.

С учётом фильтрующего свойства δ - функции имеем:

ИХ соответствует передаточ­ная функция канала:

т.е. АЧХ K(f) = γ не зависит от частоты, а ФЧХ φ(f) = - 2πft₀ линейно изменяется с часто­той.

В реальных каналах связи, даже при отсутствии аддитивного шу­ма, преобразование сигналов имеет сложный характер и обычно приводит к отличию формы выходного сигнала от входного.

Связь между энергетическими характеристиками на выходе и входе детерминированного линей­ного стационарного канала следует из определения СПМ:

где – квадрат модуля коэффициента передачи. Это выражение справедливо как для стационарной линейной системы, так и при слу­чайных стационарных воздействиях. С учетом этого ФК выходного стационарного процесса Y(t) равна:

Дисперсия выходного сигнала является результатом суммирования вкладов от спектра мощности входного сигнала, умноженного на зависящий от частоты квадрат модуля коэффициента передачи.

5.1.1.2 Прохождение случайных сигналов через детерминированные нелинейные каналы

Для нелинейных преобразований, описываемых моделью y(t) = φ[х(t)], преобразование х → у, как правило, однозначно, что не всегда можно сказать об обратном преобразовании у → х (например, квад­ратичная цепь с характеристикой у = kх²).

При нелинейных преобразованиях возникает трансформация (изменение) спектра входного воздействия. При воздействии на вход нелинейной системы случайного узкополосного сигнала с полосой частот, ограниченной F_В, и центральной частотой f₀, представляющего собой сумму регулярного сигнала и аддитивного шума x(t) = s(t) + n(t), в общем случае на выходе будут присутствовать составляющие комбинационных частот трёх видов, группирующихся около частот пf₀ (п = 0, 1, ...):

- продукты взаимо­действия составляющих входного сигнала между собой (с с);

- продукты взаи­модействия составляющих входного шума (ш ш);

- продукты взаимодействия сигнала и шума (с ш).

Разделить их на выходе системы обычно невозможно.

Если известна характеристика у = φ(х) нелинейной системы и двумерная функция распределения входного воздействия w(x₁, x₂; t₁, t₂), то основные ха­рактеристики выходного процесса (МО и ФК) в принципе всегда можно опре­делить:

,

.

Прямым преобразованием Фурье можно по ФК найти СПМ процесса Y(t).

Анализ прохождения случайных воздействий через нелинейные цепи силь­но упрощается для узкополосных воздействий, если воспользоваться их квази­гармоническим представлением.

5.1.2 Прохождение сигналов через случайные каналы связи

В простейшем случае случайное преобразование сигнала сводится к суммированию сигнала с аддитивной помехой или аддитив­ным шумом. В более сложных каналах к этому добавляются случайные изме­нения параметров канала, в результате которых принимаемый сигнал не определяется однозначно передаваемым.

В самом общем виде линейную систему (или линейный канал) можно описать случайной ИХ , представляющей случайную функцию двух аргументов: t (момента наблюдения реакции) и τ (времени, прошедшего с момента подачи δ-импульса на вход цепи). Такую ИХ имеет любая линейная система, па­раметры которой подвергаются воздействию случайных внешних воздействий, на­пример температуры, давления, влажности и т.д.

Случайный линейный канал можно характеризовать также случайной пере­даточной функцией переменных ω и t:

ФК процесса Y(t) на выходе случайного канала с такой характеристикой при подаче на вход стационарного процесса X(t) определяется выражением:

где – системная характеристика случайного канала.

Обобщая модель линейного стационарного канала для случайного входного воздействия X(t), получаем:

(5.1.1)

где параметры τ и (или) γ флуктуируют. Обычно такие флуктуации в проводных линиях связи вызываются измене­ниями внешних условий и происходят чрезвычайно медленно (т.е. за время длительности интервала , где F_с – ширина спектра сигнала, параметры канала не успевают заметно измениться) и в очень не­больших относительных пределах.

В радиоканалах при многолучёвом распро­странении радиоволн, в гидроакустических каналах флуктуации выражены более заметно. В этом случае сигнал от входа канала к его выходу проходит по параллель­ным путям (рис. 5.1.1). На выходе каждого пути сигнал имеет вид (5.1.1), но значения γ и τ для разных путей различны и в небольших пределах флуктуируют.

γ₁,τ₁

γ₂, τ₂

u (t) s(t)

γ_l, τ_l

_{Рисунок 5.1.1 – Модель многолучевого канала}

Обычно энергия волны распространяется в неоднородной среде и испытывает отражение от различных неоднородностей. Если неоднородности распределены внутри относительно небольшого отражающего или рассеивающего объёма, то разности хода (разности значений τ) для отдельных пу­тей невелики. В этом случае длительность импульса, прошедшего через такой канал, практически не увеличится. Такой канал принято назы­вать однолучевым. В этом случае наличие разных путей не вызывает существенного рассеяния (растяжения) сигна­ла во времени, но приводит к возникновению явления замираний, которое за­ключается в более или менее быстрых случайных изменениях передаточной функции канала:

,

где L – число лучей, попадающих в точку приёма; – коэффици­ент передачи по l-му лучу; τ₁ – время распространения l -го луча; – комплексный коэффициент передачи по l -му лучу.

Передаточная функция в общем случае зависит от частоты. Вследствие хаотических перемещений отражателей значения и τ_l флук­туируют, а в этом случае зависит от времени, представляя собой случайную функ­цию (мультипликативную помеху) . Во многих случаях эта функция флуктуирует значительно быстрее, чем величины и τ_l.

Важной характеристикой канала с замираниями является распределение вероятностей комплексной передаточной функции и, в первую очередь, её модуля . Для случая, когда все одного порядка и фазовые сдвиги достаточно ве­лики, одномерное распределение веро­ятности является рэлеевским:

.

Фаза результирующего сигнала θ при этом распределена равномерно на интервале (- π, +π). Дисперсия квадратурных составляющих σ² равна средней мощности приходящего сигнала. Такие зами­рания, как и каналы, в которых они проявляются, называются рэлеевскими.

Если в одном из подлучей коэффициент передачи значительно больше, чем в других, т.е. помимо диффузно отражённых лучей в место приёма приходит регулярный (не замирающий) луч, то модуль коэффициента пе­редачи канала подчиняется обобщённому распределению Рэлея:

где – отношение средних мощностей регулярной и флюктуирующих составляющих, – модифицированная функция Бесселя нулевого порядка.

Если по однолучевому каналу с замираниями передаётся относительно уз­кополос­ный сигнал, а среднеквадратическое отклонение запаздывания в от­дельных лучах удов­летворяет следующему условию:

<< , (5.1.2)

где F_c – ширина спектра сигнала, то изменения начальных фаз на разных час­тотах в спек­тре сигнала почти одинаковы. При этом все состав­ляющие спектра сиг­нала замирают одновременно, т.е. их амплитуды и фазы изме­няются одинаково. Такие за­мирания называются общими или гладкими. Ес­ли же условие (5.1.2) не выполнено, то в разных областях спектра сигнала про­цессы замираний не совпадают (частотно селективные замирания). При этом наблюдаются существенные изменения формы сигнала, что характерно для многолучевых каналов радиосвязи (приходящие в точку приёма сигналы образованы отражением от сильно разнесённых в пространстве рассеивающих объ­ёмов).

Быстрота изменений во времени комплексного случайного процесса:

(при фиксированной частоте) или скорость замираний сигнала характеризуется временем корреляции τ_кор квадратурных компонент X(t,ω) и Y(t, ω) или шириной спектра замираний .

Лекция 5.2 Модели каналов

Для математического описания канала необходимо и доста­точно указать множество входных сигналов и для любого допустимого входного сигнала задать сигнал на его выходе. Задать сигнал в виде случайного процесса (СП) можно в той или иной форме его распределения вероятностей. В непрерывном канале надо задать априор­ную плотность (многомерную) w(u) входного процесса u(t) на интервале ана­лиза T_а и многомерную условную плотность w(z/u), т.е. плотность реализа­ции принимаемого случайного колебания z(t) (сигнал + шум) при условии пе­редачи реализации u(t).

5.2.1 Идеальный канал без помех

Канал отображается линейной цепью с постоянной передаточной функци­ей, сосредоточенной в ограниченной полосе частот. Для всех непрерывных каналов допустимы любые входные сигналы, спектр которых лежит в полосе частот F_c, имеющие ограниченную среднюю мощность Р_с (либо пиковую мощность P_пик).

В идеальном канале выходной сигнал s(t) при заданном входном u(t) де­терминирован и определяется как: где – постоян­ный коэффициент передачи канала, – постоянная задержка. Эту модель ино­гда используют для описания кабельных каналов.

5.2.2 Канал с аддитивным гауссовским шумом

Сигнал на выходе такого канала равен:

(5.2.1)

где n(t) – гауссовский аддитивный шум с нулевым математическим ожидани­ем и заданной корреляционной функцией.

Чаще всего рассматривается БГШ или квазибелый с равномерной спектральной плот­ностью в полосе спектра сигнала s(t). В общем случае коэффициент передачи и запаздывание полагают известными функциями времени:

Такая модель удовлетворительно описывает многие проводные каналы, ра­диоканалы при связи в пределах прямой видимости, а также радиоканалы с медленными общими замираниями, при которых можно надёжно предсказать значения и .

5.2.3 Канал с неопределённой фазой сигнала и аддитивным шумом

Эта модель отличается от модели (5.2.1) тем, что в ней запаздывание явля­ется случайной величиной. Выра­жение для узкополосных сигналов на выходе такого канала при постоянном и случайных можно представить в виде:

где – преобразование Гильберта от u(t); – случайная фаза.

Рас­пределение вероятностей чаще всего является равномерным на интервале от 0 до 2 .

Эта модель удовлетворительно описывает те же кана­лы, что и предыдущая, если фаза сигнала в них флуктуирует. Такая флуктуа­ция вызывается небольшими изменениями протяжённости канала, свойств среды, в которой проходит сигнал, а также фазовой нестабильностью опорных генераторов.

Однолучевой гауссовский канал с общими замираниями также описывается выражением (5.2.1), в котором множитель и фаза являются СП, следовательно случайны­ми будут квадратурные компоненты При изменении квадратурных компонент X, Y во времени принимаемое ко­лебание описывается выражением:

(5.2.2)

Одномерное распределение коэффициента передачи канала может быть рэлеевским или обобщённым рэлеевским. Такие каналы называют соответственно каналами с рэлеевскими или обобщёнными рэлеевскими (или райсовскими) замираниями.

Модель однолучевого канала с замираниями достаточно хорошо описывает многие каналы ра­диосвязи в различных диапазонах волн, а также некоторые другие каналы.

Многолучевой гауссовский канал с селективными по частоте замираниями обобщает модель (5.2.2):

(5.2.3)

где N – число лучей в канале; – среднее время задержки для n-го луча.

Для модели (5.2.3) запаздывания между лучами удовлетворяют условию > . Многолучевая общая гауссовская модель хорошо описывает многие каналы ра­диосвязи.

5.2.4 Канал с межсимвольной интерференцией и аддитивным шумом

Эта модель является частным случаем случайного линейного канала, характеризующегося случайной передаточной функцией переменных и t, когда ИХ канала не зависит от t (или изменяется очень медленно), так что рассеяние по частоте практически не наблюдается. Межсимвольная интерференция (МСИ) вызывается рассеянием сигнала во времени при его прохождении по каналу связи. На выходе многолучевого канала полезный сигнал оказывается деформированным так, что одновременно присутствуют отклики канала на отрезки входного сигнала, относящиеся к довольно отдалённым моментам времени. При передаче дис­кретных сообщений это приводит к тому, что при приёме одного символа на вход приёмного устройства воздействуют также отклики на более ранние (а иногда и более поздние) символы, которые в этих случаях могут (при неопти­мальных методах приёма) проявлять себя как помехи.

МСИ вызывается нелинейностью ФЧХ канала и ограниченностью его полосы пропускания. В радиоканалах причиной МСИ чаще всего является многолучевое распространение радиоволн.

Чем больше скорость передачи символов 1/τ_с в каждом частотном канале при заданной его полосе пропускания, тем больше число соседних с анализируемым символов определяет сигнал МСИ.

5.2.5 Модели дискретного канала

Модель дискретного канала содержит множество возможных сиг­налов на его входе и распределение условных вероятностей выходного сигнала при заданном входном. Входными и выходными сигналами являются по­следовательности п кодовых символов (векторов). Поэтому для определения возможных входных сигналов достаточно указать число т различных символов (основание кода), а также длительность τ_с передачи каждого символа. Величина v =1/τ_с, определяющая количество символов, пере­даваемых в единицу времени, называется техниче­ской скоростью и измеряется в бодах. Каждый символ, поступивший на вход канала, вызывает появление одного символа на выходе, т.е. техническая скорость на входе и выходе канала одинакова.

Поразрядная разность (по модулю т) между принятым и передан­ным векторами называется вектором ошибок. Всякая единица в векторе ошибок означает, что в соответствующем месте передаваемой последо­вательности символ принят ошибочно, а всякий нуль – безошибочный приём символа. Число ненулевых символов в векторе ошибок называется его весом. Прохождение дискретного сигнала через канал можно рассматривать как сложение входного вектора с вектором ошибок. Случайный век­тор ошибок играет в дискретном канале примерно ту же роль, что и помеха в непрерывном канале. Различные модели отличаются распределением вероятностей случайного векто­ра ошибок. Преобразование помех и искажений непрерывного канала в поток ошибок происходит в модеме, осуществляющем переход от непрерывного ка­нала к дискретному.

1) Каналы без памяти

а) Постоянный симметричный канал без памяти

Постоянный симметричный канал без памяти это дискрет­ный канал, в котором каждый переданный кодовый символ может быть при­нят ошибочно с фиксированной вероятностью р и правильно с вероятностью q = 1 - р, причём в случае ошибки вместо переданного i-го символа b_i кода может быть с равной вероятностью принят любой другой символ.

Вероят­ность того, что принят символ , если был передан b_i, равна:

(5.2.4)

Термин «без памяти» означает, что вероятность ошибочного приёма симво­ла не зависит от предыстории, т.е. от того, какие символы передавались до не­го и как они были приняты. Вероятность любого n-мерного вектора ошибок в таком ка­нале равна:

где l – вес вектора ошибок.

Вероятность того, что произошло l ошибок, расположенных как угодно на про­тяжении последовательности длины п, определяется формулой Бернулли:

где – число различных сочетаний ошибок в блоке длиной п.

Эту модель называют также биномиальным каналом. Она удовлетворительно описывает канал при определённом выборе модема, отсутствии замираний в не­прерывном канале при наличии аддитивного белого или квазибелого шума. Вероятность появления оши­бок в двоичной кодовой комбинации длины п (кратному ) в биномиальном канале при р << 1 равна:

Вероятности переходов в двоичном симметричном канале схематически показаны в виде графа на рис. 4.3.1, а.

б) Двоичный симметричный канал со стиранием

Данный вид канала отличается от предыдущего тем, что алфавит на его выходе содержит дополнительный (т + 1)-й символ, обозначаемый знаком «?». Этот символ появляется то­гда, когда первая решающая схема (демодулятор) не может надёжно опознать пе­реданный символ. Вероятность такого отказа от решения или стирания симво­ла p_с в данной модели постоянна и не зависит от передаваемого символа. За счёт введения стирания удаётся значительно снизить вероятность ошибки, ино­гда её даже считают равной нулю. Вероят­ности переходов в такой модели схематически показанына рис. 5.2.1, б.

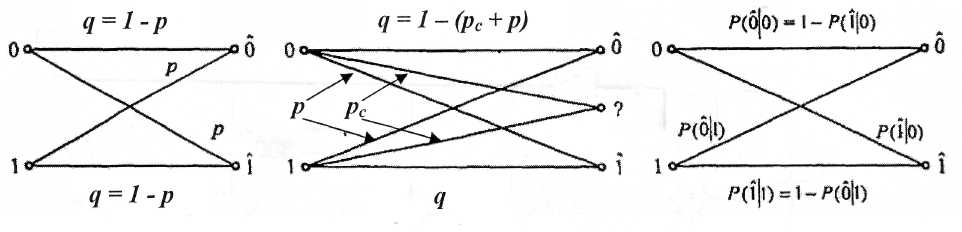
а) б) в)

Рисунок 5.2.1– Переходные вероятности в двоичных каналах:

а) симметричном, б) симметричном со стиранием,

в) несимметричном

в) Двоичный несимметричный канал

Несимметричный канал без памяти характеризуется тем, что ошибки в нём возникают независимо друг от друга, однако вероятности ошибок зависят от того, какой символ передаётся. Так условная вероятность приёма символа 1 при передаче символа 0 не равна условной вероятности приёма 0 при передаче 1 (рис. 5.2.1, в). В этой модели вероятность вектора ошибок зависит от того, какая последова­тельность символов передаётся.

2) Дискретные каналы с памятью

В таких каналах условная вероятность ошибочного приёма (i + r)-го символа при условии, что i–ый символ принят с ошибкой, не равна безусловной вероятности ошибки.

Отклонение распределения ошибок от биномиального закона в реальных каналах вызывается различными причинами:

- замираниями сигналов;

- атмосферными и взаимными помехами;

- коммутационными помехами;

- особенностями метода модуляции и демодуляции.

Простейшей моделью двоичного канала с памятью является марковская, определяемая матрицей переходных вероятностей:

,

где p₁ – условная вероятность принять (i +1)-й символ ошибочно, если пре­дыдущий принят правильно; 1- p₁ – условная вероятность принять (i + 1)-й символ правильно, если предыдущий принят правильно; p₂ – условная веро­ятность принять (i + 1)-й символ ошибочно, если предыдущий принят оши­бочно; 1 - p₂ – условная вероятность принять (i + 1)-й символ правильно, ес­ли предыдущий принят ошибочно.

Безусловная (средняя) вероятность ошибки в рассматриваемом канале рдолжна удовлетворять уравнению:

Откуда . Эта очень простая модель неточно воспроизводит свойства реальных каналов.

Более точной является модель Гильберта. Согласно этой модели канал может находиться в двух со­стояниях S₁ и S₂. В состоянии S₁ ошибок не происходит, в состоянии S₂ ошибки возникают независимо с вероятностью p₂. Переходы из одного состоя­ния в другое образуют простую марковскую цепь с матрицей переходов:

,

где p(S₂/S₁) и p(S₁/S₂) – вероятность перехода соответственно из состояния S₁ в S₂ и из состояния S₂ в S₁.

Вероятности нахождения канала в состоянии S₁ и S₂ соответственно равны:

Безусловная вероятность ошибки равна:

При использовании модели Гильберта обычно полагают р₂ = 0,5 (т.е. это состояние рассматривается как полный обрыв связи). Это хорошо согласуется с представлением о канале, в котором на некоторых временных интервалах из-за плохих условий прохождения или действия мощных помех связь «пропадает», или с представлением о проводном канале на интервале, где дей­ствуют сильные коммутационные помехи или всплески импульсных помех. Модель Гильберта можно обобщить, введя в рассмотрение вместо двух N со­стояний канала.

Относительно простую модель дискретного канала с группированием оши­бок (с памятью) предложил Пуртов. В этой модели только два параметра: веро­ятность ошибок р и показатель группирования α. В модели Пуртова зависи­мость вероятности p[≥1, n] появления искажённой комбинации (с числом ис­кажённых элементов больше или равно 1) длины n характеризуется как отношение числа иска­жённых комбинаций N_иск(n) к общему числу переданных комбинаций N(n):

.

Вероятность p[≥1, n] является неубывающей функцией от п. Согласно мо­дели Пуртова Если α = 0, то p[≥1, n] ≈ пр, что соответствует биномиальной модели. В этом случае нет пакетирования (группирования) ошибок.

Наибольшее значение α (от 0,5 до 0,7) наблюдается на кабельных линиях связи (кратковременное прерывание связи). В радиорелейных линиях (где бы­вают интервалы с большой интенсивностью ошибок и интервалы с редкими ошибками) α = 0,3 ... 0,5; для некоторых линий коротковолновой радиосвязи α = 0,3 ... 0,4.

Согласно модели Пуртова-Попова вероятность наличия комбинации дли­ной п с t и более ошибками равно:

Из этого выражения следует, что при заданном п чем больше группирование ошибок (больше t), тем меньше число искажённых кодовых комбинаций. Это очевидно, ибо при одном и том же числе ошибок пакетиро­вание приводит к их сосредоточению на отдельных комбинациях (кратность t возрастает), а число искажённых комбинаций уменьшается.

Иногда в качестве модели канала с памятью используют модель, в которой вероятность вектора ошибки не зависит от передаваемой последовательно­сти. Вероятность каждого вектора ошибок считается заданной и, вообще гово­ря, не определяется его весом. Во многих каналах из двух векторов ошибок с одинаковым весом более вероятным оказывается тот, в котором единицы расположены близко друг к другу, т.е. имеется тенденция к группированию ошибок.

Выводы по теме 5

1. Каналы связи и реализующие их электрические цепи можно разделить по характеру сигна­лов, действующих на входе и выходе, на: непрерывные, дискретные (цифровые) и дискретно-непрерыв­ные (цифро-непрерывные) или непрерывно-дискретные (не­прерывно-цифровые).

2. Классификация каналов (систем, цепей) основана на свой­ствах системных операторов, связывающих вход и выход. Различают линейные и нелинейные, стационарные и неста­ционарные, сосредоточенные системы и системы с распределён­ными параметрами.

3. Расчёт прохождения узкополосных случайных процессов через нелинейные (даже безы­нерционные) системы существенно упрощается, если воспользоваться квазигармоническим представлением входного процесса.

4. В теории и инженерной практике чаще всего пользуются следующими моделями линейного непрерывного канала: неискажающий канал с аддитивным шумом, канал с неопределённой (случайной) фазой и аддитивным шумом, однолучевой канал со случайной фазой и амплитудой (с замираниями) и аддитивным шумом, многолучевой канал с аддитивным шумом, канал с межсимвольной интерференцией (памятью) и аддитивным шумом.

5. Для любой модели дискретного канала можно ввести понятие случайного вектора ошибки как поразрядную разность между последовательностями входа и выхода. В двоичном кана­ле элементы вектора ошибки принимают значения 0 и 1. Различные модели каналов отли­чаются распределением вектора ошибки.

6. Простейшая модель дискретного канала — симметричный канал без памяти (биномиальный канал). Модель несколько усложняется введением символа стирания.

7. Простейшая модель дискретного канала с памятью – марковская модель, когда ошибки образуют простую цепь Маркова, т.е. зависят от того, правильно или ошибочно принят предыдущий символ, но не зависят от того, какой символ передаётся.

8. Дискретно-непрерывный канал характеризуется априорной вероятностью входных симво­лов и функциями правдоподобия (условными плотностями выходного сигнала) или апо­стериорными вероятностями входных символов.

Контрольные вопросы по теме 5

1. Какие два типа задач решаются при рассмотрении прохождения случайных воздействий через канал связи и его звенья?

2. Что понимается под каналом с межсимвольной интерференцией, чем определяется память такого канала?

3. Назовите основные виды моделей каналов связи.

4. Назовите основные виды моделей дискретных каналов связи.

5. Назовите причины межсимвольной интерференции.

Список литературы по теме 5

1. Теория электрической связи: Учебник для вузов /Зюко А.Г., Кловский Д.Д., Коржик В.И., Назаров М.В. - М.: Радио и связь, 1999. - 432 с.

2. Теория передачи сигналов: Учебник для вузов /Зюко А.Г., Кловский Д.Д., Назаров М.В., Финк Л.М.- М.: Связь, 1980. - 288 с.

Содержание

Предисловие	3
Список сокращений	5
Основные обозначения	7
Тема 1 Общие сведения о системах и сетях электросвязи	9
Лекция 1.1 Основы понятия о системах электросвязи. Сигналы	9
1.1.1 Основные термины и определения	9
1.1.2 Классификация сигналов	14
1.1.3 Основные параметры сигналов	17
Лекция 1.2 Системы злектросвязи	19
1.2.1 Классификация систем электросвязи	19
1.2.2 Структурная схема типичной системы электросвязи	24
1.2.3 Основные характеристики систем связи	26
1.2.4 Основы математического моделирования систем связи	29
1.2.5 Методы анализа прохождения сигналов через линейные системы	31
Лекция 1.3 Цифровое кодирование непрерывных сигналов	34
1.3.1 Дискретизация сигналов	34
1.3.2 Квантование сигналов. Импульсно-кодовая модуляция	39
Лекция 1.4 Обработка сигналов в системах передачи и приёма аналоговых и дискретных сообщений	41
1.4.1 Кодирование и модуляция	41
1.4.2 Демодуляция и декодирование	47
Лекция 1.5 Каналы связи. Помехи и искажения	49
1.5.1 Классификация каналов связи	49
1.5.2 Основные параметры каналов связи	51
1.5.3 Помехи и искажения в системах связи	52
Лекция 1.6 Сети связи	61
Выводы по теме 1	64
Контрольные вопросы по теме 1	65
Список литературы по теме 1	66
Тема 2 Математические модели сигналов и помех	67
Лекция 2.1 Математические модели детерминированных сигналов	67
2.1.1 Прямое и косвенное описание сигналов	67
2.1.2 Динамическое представление сигналов	68
2.1.3 Представление сигналов в метрических и топологиче­ских пространствах	69
2.1.4 Операторы и функционалы	75
Лекция 2.2 Разложение функций в ортогональные ряды по базисным функциям	76
2.2.1 Ортогональные системы функций и обобщенный ряд Фурье	76
2.2.2 Спектральное представление периодических функций	78
2.2.3 Спектральное представление непериодических функ­ций	80
2.2.4 Представление функций полиномами Лежандра, Чебышева, Лагерра, Эрмита, функциями Хаара, Радемахера и Уолша	82
2.2.5 Теорема Котельникова	83
Лекция 2.3 Случайные процессы и их основные характери­стики	89
2.3.1 Плотность вероятности и интегральная функция рас­пределения	90
2.3.2 Числовые характеристики	92
2.3.3 Стационарные случайные процессы	93
2.3.4 Эргодические процессы	94
2.3.5 Нормальное (гауссовское) распределение	96
Лекция 2.4 Спектральный анализ случайных процессов. Ортогональные разложения случайных функций	99
2.4.1 Спектральный анализ случайных процессов	99
2.4.2 Примеры энергетических спектров некоторых стационарных случайных процессов	100
2.4.3 Ортогональные разложения случайных функций	102
Лекция 2.5 Случайные последовательности	104
2.5.1 Марковские случайные процессы	104
2.5.2 Винеровский процесс	107
2.5.3 Представление случайных процессов дифференциаль­ными уравнениями	108
2.5.4 Модели источников сообщений, сигналов, помех	108
Лекция 2.6 Комплексное и квазигармоническое представле­ние узкополосных случайных процессов	111
2.6.1 Узкополосные процессы. Преобразование Гильберта	111
2.6.2 Огибающая и фаза случайного процесса	114
2.6.3 Функция корреляции узкополосного случайного процесса	118
2.6.4 Комплексный (аналитический) сигнал	119
Выводы по теме 2	121
Контрольные вопросы по теме 2	123
Список литературы по теме 2	124
Тема 3 Методы формирования и преобразования сигналов	126
Лекция 3.1 Преобразование колебаний в нелинейных и параметрических цепях	126
3.1.1 Классификация электрических цепей	126
3.1.2 Аппроксимация нелинейных характеристик	126
3.1.3 Усиление гармонических колебаний	128
3.1.4 Преобразование частоты	131
3.1.5 Нелинейное резонансное усиление	132
3.1.6 Параметрические цепи	133
3.1.6.1 Преобразование частоты	134
3.1.6.2 Параметрическое усиление	134
Лекция 3.2 Формирование и детектирование сигналов амплитудной модуляции	137
3.2.1 Линейная амплитудная модуляция	137
3.2.2 Использование параметрических элементов для ам­плитудной модуляции и детектирования	140
3.2.3 Использование нелинейных элементов для амплитуд­ной модуляции и детектирования	141
3.2.4 Амплитудная модуляция без несущей	142
3.2.5 Однополосная модуляция	143
3.2.6 Нелинейное (некогерентное) детектирование АМ-сиг­налов	144
Лекция 3.3 Формирование и детектирование сигналов уг­ловой модуляции	146
3.3.1 Свойства и характеристики сигналов угловой модуля­ции в частотной и временной областях	146
3.3.2 Методы формирования ЧМ и ФМ сигналов	149
3.3.3 Методы детектирования сигналов УМ	151
3.3.3.1 Синхронное (параметрическое) детектирование	151
3.3.3.2 Нелинейные схемы детектирования	151
Лекция 3.4 Формирование и детектирование сигналов, мо­дулированных дискретными сообщениями. Понятие синхро­низации и принципы ее обеспечения в системах электросвязи	154
3.4.1 Модуляция и детектирование импульсных переносчи­ков	154
3.4.2 Методы вторичной модуляции и демодуляции	158
3.4.3 Синхронизация в системах электросвязи	160
Выводы по теме 3	162
Контрольные вопросы по теме 3	163
Список литературы по теме 3	164
Тема 4 Цифровая обработка сигналов	165
Лекция 4.1 Общие понятия. Спектр дискретного сигнала	165
4.1.1 Обобщённый алгоритм цифровой обработки сигналов	165
4.1.2 Спектр дискретного сигнала	169
Лекция 4.2 Методы исследования линейных стационарных цифровых систем	171
4.2.1 Временные и спектральные методы	171
4.2.2 Разностные уравнения	171
4.2.3 Применение z-преобразования в задачах анализа и синтеза цифровых систем	174
Лекция 4.3 Синтез цифровых фильтров	176
4.3.1 Нерекурсивные цифровые фильтры	176
4.3.2 Рекурсивные цифровые фильтры	177
4.3.3 Устойчивость рекурсивных цифровых фильтров	178
4.3.4 Синтез цифровых фильтров по заданной импульсной и частотной характеристике аналогового прототипа	179
4.3.5 Синтез цифровых фильтров путём дискретизации дифференциаль­ного уравнения аналогового прототипа	181
4.3.6 Погрешности цифровой фильтрации	181
Выводы по теме 4	182
Контрольные вопросы по теме 4	183
Список литературы по теме 4	184
Тема 5 Математические модели каналов связи. Преобразование сигналов в каналах связи	185
Лекция 5.1 Общие сведения о каналах связи	185
5.1.1 Прохождение случайных сигналов через детерминированные линейные и нелинейные каналы	185
5.1.1.1 Прохождение случайных сигналов через линейные каналы	185
5.1.1.2 Прохождение случайных сигналов через детерминированные нелинейные каналы	186
5.1.2 Прохождение сигналов через случайные каналы связи	187
Лекция 5.2 Модели каналов	191
5.2.1 Идеальный канал без помех	191
5.2.2 Канал с аддитивным гауссовским шумом	191
5.2.3 Канал с неопределённой фазой сигнала и аддитивным шумом	192
5.2.4 Канал с межсимвольной интерференцией и аддитив­ным шумом	193
5.2.5 Модели дискретного канала	194
Выводы по теме 5	199
Контрольные вопросы по теме 5	200
Список литературы по теме 5	201