
- •Теория электрической связи
- •Часть 1
- •Тема 1 Общие сведения о системах и сетях электросвязи
- •Тема 2 Математические модели сигналов
- •Тема 3 Методы формирования и преобразования сигналов
- •Тема 4 Цифровая обработка сигналов
- •Тема 5 Математические модели каналов связи. Преобразование сигналов в каналах связи
Тема 4 Цифровая обработка сигналов
Лекция 4.1 Общие понятия. Спектр дискретного сигнала
4.1.1 Обобщённый алгоритм цифровой обработки сигналов
Цифровая обработка сигналов (ЦОС) – это область науки и техники, в которой изучаются общие для различных технических приложений принципы, методы и алгоритмы обработки сигналов средствами цифровой вычислительной техники.
Благодаря своим достоинствам ЦОС находит большое применение в современных системах связи. Её существенными преимуществами по сравнению с аналоговой обработкой являются:
- значительно более высокая точность обработки сигналов;
- возможность гибкой оперативной перестройки алгоритмов обработки сигналов, обеспечивающая создание многорежимных устройств и реализацию адаптивных систем;
- высокая технологичность изготовления устройств ЦОС;
- высокая степень совпадения и повторяемости характеристик устройств с расчётными характеристиками;
- большие возможности автоматизации проектирования устройств ЦОС;
- высокостабильные эксплуатационные характеристики устройств ЦОС.
Обобщенная схема ЦОС, отображающая последовательность процедур, необходимых для преобразования исходного аналогового сигнала х(t) в другой аналоговый сигнал y(t) по заданному алгоритму средствами цифровой вычислительной техники, представлена на рис. 4.1.1
В ЦОС существует три основных этапа:
- формирование цифровогосигнала хц(пТд) из исходного аналогового сигнала x(t);
- преобразование цифрового сигнала хц(пТд) в цифровой сигнал уц(пТд) по заданному алгоритму;
- формирование результирующего аналогового сигнала y(t) из цифрового сигнала уц(пТд).

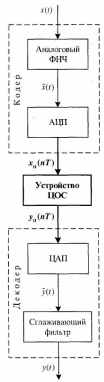
Рисунок 4.1.1 – Обобщенная схема цифровой обработки сигнала
В обобщенной схеме ЦОС этим этапам соответствуют трифункциональных устройства: кодер, устройство ЦОС и декодер.
Временные диаграммы поэтапного процесса ЦОС приведены на рис. 4.1.1, а – е.
1) На первомэтапе кодериз исходного аналоговогосигнала x(t) (рис. 4.1.1, а) формирует цифровойсигнал хц(пТд) (рис. 4.1.1, б). В состав кодера входят аналоговый фильтр нижних частот (ФНЧ) и аналого-цифровой преобразователь (АЦП).
ФНЧ предназначен
для ограничения спектра
исходного
аналогового сигнала x(t).
Необходимостьограничения спектра
вытекает из теоремы Котельникова, в
соответствии с которой частота
дискретизации fд
выбирается из условия:
 ,
где Fв – верхняя
частота спектра сигнала. На выходе ФНЧ
получают аналоговый сигнал
,
где Fв – верхняя
частота спектра сигнала. На выходе ФНЧ
получают аналоговый сигнал
 с финитным (ограниченным по частоте)
спектром
с финитным (ограниченным по частоте)
спектром
 (рис. 4.1.1 б).
(рис. 4.1.1 б).
АЦП формирует
цифровой сигнал хц(пТд)
посредством дискретизации и
квантования сигнала
(рис. 4.1.1, в). Дискретизация
по времени (дискретизация) представляет
собой процедуру взятия мгновенных
значений – отсчетов аналогового сигнала
x(t)
с интервалом времени, равным периоду
дискретизации Тд. Значения
отсчетов х(пТд) совпадают
со значениями сигнала
в моменты времени
 :
:
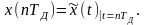
Совокупность отсчетов х(пТд), n = 0. 1,..., называют дискретным сигналом.
Квантование по уровню (квантование) производится с целью представления точных значений отсчетов х(пТд) в виде двоичных чисел конечной разрядности – квантованных отсчетов хц(пТд). Для этого динамический диапазон дискретного сигнала х(пТд) разбивается на конечное число дискретных уровней – уровней квантования – и каждому отсчету по определенному правилу присваивается значение одного из ближайших уровней, между которыми он оказывается. Уровни квантования кодируются двоичными числами разрядности m, зависящей от числа уровней квантования Nкв ≤ 2m, откуда m = int(log2Nкв). На временной диаграмме (рис. 4.1.1, в) для примера выбрано 5 уровней квантования (без учета знака), поэтому m = 3 и отсчеты хц(пТд) кодируются четырехразрядными двоичными числами: один разряд знаковый, три значащих. Совокупность квантованных отсчетов хц(пТд), n = 0, 1,..., называют цифровым сигналом.
2) На втором этапе устройство ЦОС преобразует цифровойсигнал хц(пТд) (рис. 4.1.1, в) в цифровойсигнал уц(пТд) (рис. 4.1.1, г) по заданному алгоритму.
3) На третьем этапе декодер формирует результирующий аналоговый сигнал y(t) из цифрового сигнала уц(пТд). В состав декодера входят цифро-аналоговый преобразователь (ЦАП) и сглаживающий фильтр.
ЦАП формирует из цифрового сигнала уц(пТд) (рис. 4.1.1 г) ступенчатый аналоговый сигнал y(t) (рис. 4.1.1 д).
Низкочастотный сглаживающий фильтр устраняет ступенчатый эффект (скачки) в выходном сигнале ЦАП y(t). На выходе сглаживающего фильтра получаем аналоговый сигнал y(t) – результат преобразования исходного сигнала x(t) (рис. 4.1.1 е).
Наиболее широкое применение нашли линейные системы ЦОС, в которых имеет место суперпозиция и однородность, или гомогенность (отклик на входной сигнал, усиленный в определенное число раз, будет усилен в то же число раз).
Если входной сигнал x(t-t0) порождает одинаковый выходной сигнал y(t-t0) при любом сдвиге t0, то систему называют инвариантной во времени. Её свойства можно исследовать в любые произвольные моменты времени. Для описания линейной системы вводится специальный входной сигнал – единичный импульс (δ-импульс). В силу свойства суперпозиции и однородности любой входной сигнал можно представить в виде суммы таких импульсов, подаваемых в разные моменты времени и умноженных на соответствующие коэффициенты. Выходной сигнал системы в этом случае представляет собой сумму откликов на эти импульсы, умноженных на указанные коэффициенты. Отклик на единичный импульс называют импульсной характеристикой системы h(k), а отклик на произвольный входной сигнал х(n) можно выразить сверткой y(n) = h(k)*х(n-k).
К линейным устройствам ЦОС относятся различные фильтры, цифровые модуляторы и демодуляторы, построенные на основе перемножения двух функций.
4.1.2 Спектр дискретного сигнала
В основе одного из основных методов обработки сигналов, в зависимости от их видов, лежит четыре варианта преобразования Фурье – преобразование и ряд Фурье с непрерывным или дискретным временем. При этом преобразование предполагает непрерывное, а ряд – дискретное распределение частот.
Дискретный сигнал:
 ,
(4.1.1)
,
(4.1.1)
где
 – безразмерная периодическая (с периодом
– безразмерная периодическая (с периодом
 решётчатая функция, имеет спектр по
Фурье:
решётчатая функция, имеет спектр по
Фурье:
 (4.1.2)
(4.1.2)
где
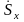 – спектр Фурье исходного непрерывного
сигнала
,
т.е. спектр дискретного сигнала повторяется
с периодом
– спектр Фурье исходного непрерывного
сигнала
,
т.е. спектр дискретного сигнала повторяется
с периодом
 .
.
Если отдельные
копии данного спектра взаимно не
перекрываются ( ,
то из спектра
,
то из спектра
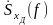 можно восстановить без искажений
не только спектр исходного сигнала
можно восстановить без искажений
не только спектр исходного сигнала
 ,
но и сам непрерывный сигнал
.
,
но и сам непрерывный сигнал
.
Спектр Фурье дискретного финитного сигнала:

 ,
(4.1.3)
,
(4.1.3)
определённого на
интервале (0,Т), можно найти, используя
периодический сигнал
 ,
совпадающий с
,
совпадающий с
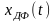 на интервале (0,Т), для которого
комплексные амплитуды
определяются формулой:
на интервале (0,Т), для которого
комплексные амплитуды
определяются формулой:
 (4.1.4)
(4.1.4)
Эта формула
определяет коэффициенты дискретного
преобразования Фурье (ДПФ). Из неё
следует, что при заданных N
отсчётах
 существуют
N коэффициентов
ДПФ (n = 0, 1, …, N
- 1). Коэффициент
существуют
N коэффициентов
ДПФ (n = 0, 1, …, N
- 1). Коэффициент
 определяет постоянную составляющую.
При чётном N из (5.1.4)
для вещественных
следует:
определяет постоянную составляющую.
При чётном N из (5.1.4)
для вещественных
следует:

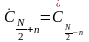 n
= 1, 2, …,
n
= 1, 2, …,
 ,
(4.1.5)
,
(4.1.5)
т.е. коэффициенты
ДПФ с симметричными относительно
 номерами, образуют комплексно-сопряжённые
пары. Число амплитуд
номерами, образуют комплексно-сопряжённые
пары. Число амплитуд
 ,
образующих спектр ДПФ, равно
.
При заданных
(k = 0, 1, …, N
- 1)
можно найти обратным ДПФ (ОДПФ):
,
образующих спектр ДПФ, равно
.
При заданных
(k = 0, 1, …, N
- 1)
можно найти обратным ДПФ (ОДПФ):
 .
(4.1.6)
.
(4.1.6)
ДПФ и ОДПФ удовлетворяют условию линейности.
При вычислении N
коэффициентов ДПФ и ОДПФ необходимо
выполнить
 наиболее трудоёмких операций умножения.
Разработанные в настоящее время
алгоритмы быстрого преобразования
Фурье (БПФ) позволяют существенно
сократить число членов массива
обрабатываемых данных и, следовательно,
операций умножения, которое не превышает
наиболее трудоёмких операций умножения.
Разработанные в настоящее время
алгоритмы быстрого преобразования
Фурье (БПФ) позволяют существенно
сократить число членов массива
обрабатываемых данных и, следовательно,
операций умножения, которое не превышает
 ,
что при больших N
существенно меньше, чем
.
,
что при больших N
существенно меньше, чем
.
Известное применение находят и другие варианты преобразования Фурье: косинусное для чётных и синусное для нечётных сигналов, а также преобразование Хартли, где базисными функциями являются суммы синусов и косинусов, что позволяет повысить производительность вычислений и избавиться от комплексной арифметики. Вместо косинусных и синусных функций используются также меандровые функции Уолша, принимающие значения только +1 и -1.
Лекция 4.2 Методы исследования линейных стационарных цифровых систем
4.2.1 Временные и спектральные методы
Для исследования
линейных стационарных цифровых систем
(ЛСЦС) по аналогии с аналоговыми
применяются временные и спектральные
методы. В первом случае отклик ЛСЦС
y(nTд)
на произвольное внешнее воздействие
x(nTд)
можно найти через её импульсную
характеристику (ИХ) h(t)
с помощью цифрового аналога
свёртки
 (интеграла Дюамеля), получаемого
путём дискретизации переменных τ
и t (τ = nTд,
t = mTд):
(интеграла Дюамеля), получаемого
путём дискретизации переменных τ
и t (τ = nTд,
t = mTд):
 (4.2.1)
(4.2.1)
где h(l), l = 0, 1, 2, …, L – отсчёты ИХ ЛСЦС, т.е. отклика на единичный импульс (1, 0, 0, 0, …), поступивший на вход ЛСЦС в момент времени t = 0.
Для физически реализуемой системы h(-l) = 0, l = 1, 2, …, и суммирование в (4.2.1) фактически выполняется для n ≤ m, т.е.:
 (4.2.2)
(4.2.2)
При числе входных отсчётов, равном N, а числе отсчётов ИХ ЛСЦС, равном L + 1, m в последнем выражении принимает значения 0, 1, 2, …, NΣ – 1 (NΣ = N +L). Для нахождения одного значения y(mTд) надо выполнить не более чем L + 1 операций умножения, а для нахождения всех значений y(mTд) – примерно NΣ (L+1) операций умножения.
Число операций существенно сокращается при использовании спектрального метода анализа и методов БПФ.
4.2.2 Разностные уравнения
Эффективные способы построения линейных систем с постоянными параметрами (ЛПП – систем) могут быть найдены при их описании разностными уравнениями (РУ). По РУ можно определить многие характеристики рассматриваемой системы. Важное значение РУ состоит в том, что они непосредственно определяют способ построения цифровой системы.
Линейное РУ М-го порядка с постоянными коэффициентами, описывающее физически реализуемую систему, имеет вид:
 n
≥ 0. (4.2.3)
n
≥ 0. (4.2.3)
где коэффициенты {bi} и {ai} описывают конкретную систему, причём aМ ≠ 0. Данное уравнение удобно решать методом прямой подстановки. Имея набор начальных условий (например, x(i), y(i) для i = -1, -2, …, -М) и входную последовательность x(n) = x(nТД), по данной формуле можно непосредственно вычислить выходную последовательность y(n) для n ≥ 0.
Более эффективно решение РУ в явном виде, преимущество которого состоит в том, что оно позволяет просто определить y(n) для любого конкретного n = n0. Основная идея сводится к получению двух решений уравнения: однородного и частного. Однородное решение получается путём подстановки нулей вместо членов, содержащих элементы входной последовательности x(n) и определения отклика при нулевой входной последовательности. Этот класс решений описывает основные свойства заданной системы. Частное решение получают путём подбора вида последовательности y(n) на выходе при заданной входной последовательности x(n). Для определения произвольных постоянных однородного решения используются начальные условия. Например, разностное уравнение:
y(n) = x(n) – 3y(n – 1) (4.2.4)
с начальными условиями y(-1) = 0 и x(n) = n2 + n при решении методом прямой подстановки даёт:


Решим это же уравнение вторым методом, учитывая, что характеристическими решениями такого класса уравнений являются решения вида Aan.
Однородное решение получим преобразовав уравнение (4.2.4) при х(n) = 0 и произведя замену y(n) = Aan:
 (4.2.5)
(4.2.5)
Частным решением, соответствующим x(n) = n2 + n, является решение вида:
 (4.2.6)
(4.2.6)
Подставив (4.2.6) в уравнение (4.2.4) получаем:
 (4.2.7)
(4.2.7)
Из условия равенства коэффициентов при равных степенях n получаем:


 (4.2.8)
(4.2.8)
а общее решение имеет вид:
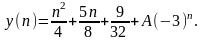 (4.2.9)
(4.2.9)
Коэффициент
А
определяется из начального условия
y(-1)
= 0, откуда
 и:
и:
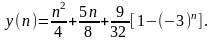 (4.2.10)
(4.2.10)
Выборочная проверка данного решения при n ≥ 0 показывает полное совпадение с прямым решением.
4.2.3 Применение z-преобразования в задачах анализа и синтеза цифровых систем
При математическом
описании дискретных последовательностей,
а также дискретных цепей большую роль
играет функция
 .
Изображения по Лапласу временных
процессов, а также передаточных
функций цепей, в которые входят функции
.
Изображения по Лапласу временных
процессов, а также передаточных
функций цепей, в которые входят функции
 ,
оказываются трансцендентными функциями
p, что существенно
затрудняет анализ. Его можно упростить
при переходе к новой переменной z,
связанной с p
соотношением:
,
оказываются трансцендентными функциями
p, что существенно
затрудняет анализ. Его можно упростить
при переходе к новой переменной z,
связанной с p
соотношением:

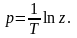
При такой замене указанные функции от p преобразуются в рациональные функции от переменной z, благодаря чему упрощается представление их на плоскости z.
Z - преобразование очень полезно при исследовании дискретных ЛПП-систем. Это преобразование можно получить из преобразования Лапласа или Фурье дискретного сигнала хд(n). Для последовательности хд(n), заданной при всех n, оно определяется следующим образом:
 (4.2.11)
(4.2.11)
где
 – комплексная переменная.
– комплексная переменная.
Z –
преобразование последовательности
можно рассматривать как способ её
однозначного представления в комплексной
z - плоскости. При
 из последнего выражения следует
преобразование Фурье исходной
последовательности:
из последнего выражения следует
преобразование Фурье исходной
последовательности:
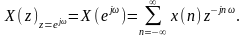 (4.2.12)
(4.2.12)
Z – преобразования обладают следующими основными свойствами:
- линейность: если X1(z) и X2(z) являются z – преобразованиями последовательностей х1(n) и х2(n), то при любых действительных a и b z – преобразование последовательности ax1(n) + bx2(n) равно aX1(z) + bX2(z);
- задержка: если
последовательность х1(n)
имеет z - преобразование
X1(z),
то z – преобразование
последовательности x1(n
- n0) равно
 при любых n0;
при любых n0;
- свёртка: если
х (n) и
 y(n)
являются входной и выходной
последовательностью дискретной
ЛПП - системы с ИХ h(n),
то Y(z)
= X(z)H(z),
где X(z),
Y(z)
и H(z)
– соотвествтенно z -
преобразования последовательностей
y(n)
являются входной и выходной
последовательностью дискретной
ЛПП - системы с ИХ h(n),
то Y(z)
= X(z)H(z),
где X(z),
Y(z)
и H(z)
– соотвествтенно z -
преобразования последовательностей
 ,
y(n)
и
,
y(n)
и
 ;
;
- перемножение последовательностей: если X1(z) и X2(z) являются z – преобразованиями последовательностей х1(n) и х2(n), то последовательность x3(n) = x1(n)x2(n) имеет z – преобразование:
 ,
,
где R – замкнутая кривая контура интегрирования, лежащая внутри пересечения областей сходимости функций X1(v) и X2(z/v).
Отклик ЛПП –
системы на гармоническую последовательность
 определяется свёрткой:
определяется свёрткой:

где
 –
ЧХ (передаточная функция) ЛСЦС,
зависящая от частоты
,
шага дискретизации TД
и ИХ ЛСЦС
–
ЧХ (передаточная функция) ЛСЦС,
зависящая от частоты
,
шага дискретизации TД
и ИХ ЛСЦС

 l – n
= m, h(m)
= 0 при m <
0
l – n
= m, h(m)
= 0 при m <
0 .
.
ЧХ ЛСЦС – периодическая функция fД = 1/TД.
Введя
 ,
получим z –
преобразование ИХ ЛСЦС:
,
получим z –
преобразование ИХ ЛСЦС:
 (4.2.13)
(4.2.13)
называемое системной функцией (СФ) ЛСЦС.
Лекция 4.3 Синтез цифровых фильтров
Цифровые фильтры (ЦФ) с заданной передаточной функцией можно построить различными способами. Все фильтры можно разделить на два больших класса: рекурсивные и нерекурсивные. Для рекурсивных цифровых фильтров (РЦФ) текущий отсчёт отклика y(n) определяется текущим и предшествующими значениями входной последовательности {x(n)} и предшествующими отсчётами отклика:

Числа L и M в данном разностном уравнении называются соответственно памятью (относительной) ЦФ по входу и выходу.
В нерекурсивных цифровых фильтрах (НЦФ) текущий отсчёт отклика зависит от текущего и предшествующих значений входной последовательности (отсутствует память по выходу):
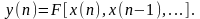 (4.3.2)
(4.3.2)
4.3.1 Нерекурсивные цифровые фильтры
В этом случае РУ принимает вид:
 (4.3.3)
(4.3.3)
Структурная схема НЦФ, реализующая алгоритм в соответствии с данным РУ, представлена на рис. 4.3.1.
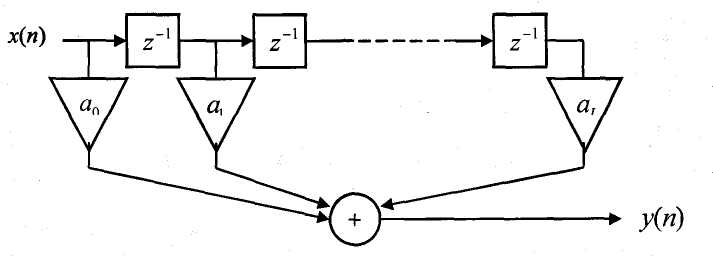
Рисунок 4.3.1 – Структурная схема НЦФ
Основными элементами ЦФ являются блоки задержки отсчётных значений на один тактовый интервал (условно они обозначены символом z-1), а также масштабные блоки. Сигналы с последних суммируются, образуя отсчёт.
Используя РУ (4.3.3) можно построить только ЦФ с конечной ИХ [h(0), h(1), h(2), …, h(L)].
Выполнив z - преобразование левой и правой части РУ (4.3.3), получим:
 (4.3.4)
(4.3.4)
и СФ данного фильтра:
 (4.3.5)
(4.3.5)
Данная дробно-рациональная функция от z имеет L- кратный полюс при z = 0 и L нулей, определяемых корнями полинома числителя, которые зависят от отсчётов ИХ ЦФ h(l) = a1. Выражение для ЧХ фильтра имеет вид:
 (4.3.6)
(4.3.6)
4.3.2 Рекурсивные цифровые фильтры
Структурная схема РЦФ, реализующая общий алгоритм (4.3.1), представлена на рис. 4.3.2.
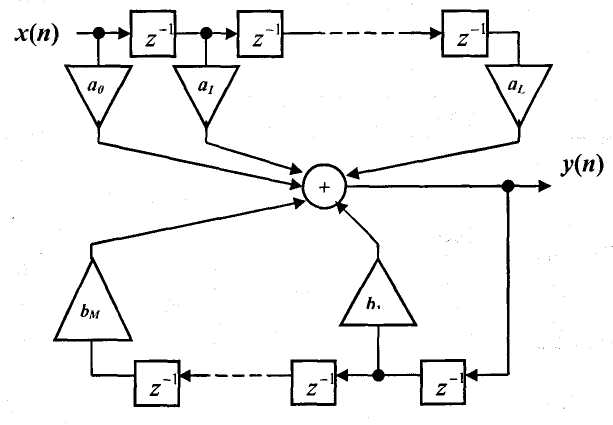
Рисунок 4.3.2 – Структурная схема РЦФ
Выполнив z - преобразование левой и правой части РУ (4.3.1), получим:
 (4.3.7)
(4.3.7)
откуда следует выражение для СФ РЦФ:
 M
> L. (4.3.8)
M
> L. (4.3.8)
4.3.3 Устойчивость рекурсивных цифровых фильтров
За счёт наличия обратной связи с выхода на вход РЦФ обладает неограниченной ИХ. Такая система требует исследования на устойчивость. ЦФ устойчив, если |y(n)| при n → ∞ не превышает некоторого положительного числа A, независимо от начальных условий в системе. Используя уравнение (4.3.1) при отсутствии внешнего воздействия, проведём анализ свободных колебаний:
 (4.3.9)
(4.3.9)
Отдельное свободное
колебание в линейной стационарной
системе определяется выражением
 ,
т.е. при t = nTД
имеем
,
т.е. при t = nTД
имеем
 .
Обозначив
.
Обозначив
 ,
найдём решение в виде
,
найдём решение в виде
 ,
подставив которое в исходное уравнение,
получим характеристическое уравнение,
определяющее
:
,
подставив которое в исходное уравнение,
получим характеристическое уравнение,
определяющее
:
 (4.3.10)
(4.3.10)
Данному уравнению
удовлетворяют полюсы СФ РЦФ. При
найденных корнях этого уравнения
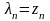 ,
,
 ,
общее решение уравнения (4.3.10) можно
представить в виде:
,
общее решение уравнения (4.3.10) можно
представить в виде:
 (4.3.11)
(4.3.11)
где ограниченные коэффициенты А1, А2, …, АМ определяются начальными условиями.
Фильтр будет устойчив, если все полюсы СФ H(z) (4.3.8) удовлетворяют условию:

 ,
(4.3.12)
,
(4.3.12)
т.е. лежат внутри единичного круга с центром в точке z = 0 , т.к. в этом случае все свободные колебания во времени определяются членами бесконечно убывающей геометрической прогрессии.
4.3.4 Синтез цифровых фильтров по заданной импульсной и частотной характеристике аналогового прототипа
В основе синтеза лежит предположение о том, что синтезируемый ЦФ должен обладать ИХ, являющейся результатом дискретизации ИХ соответствующего аналогового прототипа h(n) = h(nTд). Число отдельных членов в выражении ИХ ЦФ может быть как конечным, так и бесконечным. Это определяет структуру ЦФ: ИХ с конечным числом отсчётов соответствует НЦФ, для реализации неограниченно протяжённой ИХ требуется РЦФ.
Связь между коэффициентами ИХ и структурой ЦФ особенно проста для НЦФ. В общем случае синтез структуры ЦФ осуществляется путём применения z-преобразования к последовательности вида h(n) = h(nTд). Найдя СФ H(z) ЦФ, следует сравнить её с общим выражением для СФ РЦФ (4.3.8) и определить коэффициенты нерекурсивной и рекурсивной частей.
Степень приближения
ЧХ синтезируемого ЦФ к характеристикам
аналогового прототипа зависит от
выбранного шага дискретизации Тд.
ЧХ ЦФ вычисляется путём замены в СФ
z = exp(jωTд) .
.
Рассмотрим пример
синтеза ЦФ аналогового прототипа
интегратора (звено 1-го порядка) с ИХ
h(t)
= ae-at,
(a > 0), t
≥ 0). ЧХ этого фильтра
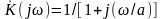 .
При построении ЦФ по двум отсчётам a,
.
При построении ЦФ по двум отсчётам a,
 его СФ и ЧХ равны:
его СФ и ЧХ равны:


При построении
РЦФ по всем отсчётам
,
(n
= 0, 1, 2, …) его СФ
 сходится при
сходится при
 и равна:
и равна:
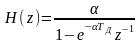 ,
,
а ЧХ РЦФ первого порядка (с памятью М = 1) равна:
 .
.
Создать ЦФ, ЧХ
которого в точности повторяли бы ЧХ
аналогового прототипа, принципиально
не возможно, так как Kцф(jω)
является периодической функцией частоты
с периодом, определяемым шагом
дискретизации Тд. Однако можно
потребовать, чтобы весь интервал
частот аналогового прототипа ωa
был преобразован в отрезок частот
ωц ЦФ, на котором
сохраняется форма характеристики K(jω),
причём
 .
Формальный переход от ЧХ аналогового
прототипа к СФ ЦФ возможен с использованием
соотношений
.
Формальный переход от ЧХ аналогового
прототипа к СФ ЦФ возможен с использованием
соотношений
 или
или
 .
Однако в этом случае получается физически
нереализуемая СФ ЦФ. В связи с этим для
синтеза ЦФ получило распространение
билинейное преобразование:
.
Однако в этом случае получается физически
нереализуемая СФ ЦФ. В связи с этим для
синтеза ЦФ получило распространение
билинейное преобразование:
 (4.3.13)
(4.3.13)
Характерной
особенностью этого закона преобразования
является то, что использование замены
переменной

 позволяет
получить:
позволяет
получить:

 ,
,
откуда вытекает соотношение между текущими частотами ωa и ωц аналоговой и цифровой систем:

 (4.3.14)
(4.3.14)
Если
частота дискретизации достаточно велика
(ωцTД
<< 1) ,
то ωa
≈ ωц.
Т.о., на низких частотах характеристики
аналогового и ЦФ практически совпадают.
В общем случае необходимо принимать
во внимание трансформацию масштаба по
оси частот ЦФ (4.3.14).
,
то ωa
≈ ωц.
Т.о., на низких частотах характеристики
аналогового и ЦФ практически совпадают.
В общем случае необходимо принимать
во внимание трансформацию масштаба по
оси частот ЦФ (4.3.14).
Практически процедура синтеза ЦФ состоит в том, что в ЧХ Ка(р) аналогового прототипа производится замена переменной по формуле (4.3.13). Полученная при этом СФ ЦФ оказывается дробно-рациональной и поэтому позволяет непосредственно записать алгоритм цифровой фильтрации.
4.3.5 Синтез ЦФ путём дискретизации дифференциального уравнения аналогового прототипа
Построение ЦФ сводится к переходу от заданного дифференциального уравнения к РУ.
Если аналоговая система описывается уравнением:
 (4.3.15)
(4.3.15)
то заменив в нём производные конечными разностями:


получим РУ:

где



Полученное уравнение
реализуется РЦФ второго порядка (М
= 2) с СФ
 и ЧХ
и ЧХ .
.
4.3.6 Погрешности цифровой фильтрации
Погрешности работы
ЦФ обусловлены квантованием уровней
сигнала. Квантованные отсчёты xкв(n)
описывают мгновенные значения
аналогового дискретного сигнала x(n)
с определённой погрешностью (шумом
квантования):
 ,
которая уменьшается (по модулю) с
уменьшением шага квантования
,
которая уменьшается (по модулю) с
уменьшением шага квантования
 (xmax,
xmin
– соответственно наибольшее и наименьшее
значения входного сигнала, Nкв
– количество уровней квантования).
В качестве дискретного принимается
уровень, ближайший к истинному. В этих
условиях погрешность
(xmax,
xmin
– соответственно наибольшее и наименьшее
значения входного сигнала, Nкв
– количество уровней квантования).
В качестве дискретного принимается
уровень, ближайший к истинному. В этих
условиях погрешность
 лежит в пределах
лежит в пределах
 .
Случайная погрешность
.
Случайная погрешность
 равномерно распределена в интервале
равномерно распределена в интервале
 ,
её математическое ожидание равно
нулю, а дисперсия
,
её математическое ожидание равно
нулю, а дисперсия
 .
Дискретный выходной отсчёт ЦФ,
обусловленный шумом квантования
,
равен
.
Дискретный выходной отсчёт ЦФ,
обусловленный шумом квантования
,
равен
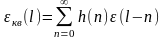 .
Математическое ожидание выходного шума
рано нулю, дисперсия
.
Математическое ожидание выходного шума
рано нулю, дисперсия
 .
Относительная погрешность ЦФ,
обусловленная шумом квантования,
определяется следующим выражением:
.
Относительная погрешность ЦФ,
обусловленная шумом квантования,
определяется следующим выражением:
 .
(4.3.16)
.
(4.3.16)
Выходной шум ЦФ, обусловленный квантованием сигнала, тем меньше, чем быстрее убывают отсчёты ИХ ЦФ.
Выводы по теме 4
1. Устройство ЦОС обладает рядом преимуществ перед устройствами обработки сигналов в непрерывном времени и широко применяется на практике в системах передачи как дискретных, так и непрерывных сообщений.
Особенно широко применяются в системах связи линейные стационарные ЦФ и цифровые перемножители.
Спектр Фурье дискретного сигнала является периодической функцией частоты дискретизации.
4. Линейчатый спектр
дискретного финитного (периодического)
сигнала с числом отчётов N определяется
дискретным преобразованием Фурье
(ДПФ). Число компонент такого спектра
 равно
N, а число амплитуд
N/2. По спектральным
компонентам
дискретные
отсчёты сигнала х(k)
определяются через ОДПФ.
равно
N, а число амплитуд
N/2. По спектральным
компонентам
дискретные
отсчёты сигнала х(k)
определяются через ОДПФ.
Существуют методы быстрого преобразования Фурье (БПФ), позволяющие существенно сократить число операций, выполняемых при расчёте ЦФ спектральными методами.
При анализе и синтезе ЦФ широко используется z-преобразование для получения спектральных характеристик входного и выходного сигналов и самого цифрового фильтра (его системной функцией H(z)). Обратным z-преобразованием определяются временные характеристики входных и выходных сигналов, а также ЦФ.
Частотный коэффициент передачи ЦФ определяется системной функцией фильтра при
 .
.Линейные стационарные цифровые фильтры с финитной импульсной характеристикой реализуются нерекурсивной схемой, а с неограниченной импульсной характеристикой – рекурсивной схемы (с обратной связью с выхода на вход).
ЦФ часто строятся по аналоговому эквиваленту. Находят применение методы синтеза ЦФ по заданным импульсной характеристике, дифференциальному уравнению, п частотной характеристике аналогового эквивалента.
Контрольные вопросы по теме 4
Изобразите обобщённую схему цифровой обработки сигналов и поясните суть происходящих в ней процессов.
Назовите три основных этапа цифровой обработки сигналов.
Что такое цифровой фильтр?
Запишите разностное уравнение для ЦФ.
Что такое импульсная реакция ЦФ?
Что такое переходная характеристика ЦФ?
Что такое передаточная функция ЦФ?
Что такое z-преобразование заданного процесса?
Список литературы по теме 4
1. Теория электрической связи: Учебник для вузов /Зюко А.Г., Кловский Д.Д., Коржик В.И., Назаров М.В. - М.: Радио и связь, 1999. - 432 с.
2. Гоноровский И.С. Радиотехнические цепи и сигналы. - М.: Радио и связь, 1986. - 512 с.
3. Баскаков С.И. Радиотехнические цепи и сигналы. Учебник для вузов. – М.: Высш. шк., 2005. – 462 с.
4. Л. Рабинер, Б. Гоулд. Теория и применение цифровой обработки сигналов / Пер. с англ. под ред. Ю.А. Александрова. – М.: Мир, 1978.
