
- •Теория электрической связи
- •Часть 1
- •Тема 1 Общие сведения о системах и сетях электросвязи
- •Тема 2 Математические модели сигналов
- •Тема 3 Методы формирования и преобразования сигналов
- •Тема 4 Цифровая обработка сигналов
- •Тема 5 Математические модели каналов связи. Преобразование сигналов в каналах связи
Тема 3 Методы формирования и преобразования сигналов
Лекция 3.1 Преобразование колебаний в нелинейных и параметрических цепях
3.1.1 Классификация электрических цепей
Любая электрическая цепь описывается дифференциальным уравнением:
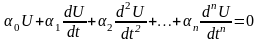 .
(3.1.1)
.
(3.1.1)
При
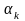 =
const электрическая цепь
называется линейной (ЛЭЦ). Она
состоит из линейных элементов:
сопротивления R,
индуктивности L и
ёмкости C. Для линейной
цепи справедлив принцип суперпозиции.
В спектре сигнала, прошедшего через
ЛЭЦ, невозможно появление новых частот,
не содержащихся в спектре входного
сигнала.
=
const электрическая цепь
называется линейной (ЛЭЦ). Она
состоит из линейных элементов:
сопротивления R,
индуктивности L и
ёмкости C. Для линейной
цепи справедлив принцип суперпозиции.
В спектре сигнала, прошедшего через
ЛЭЦ, невозможно появление новых частот,
не содержащихся в спектре входного
сигнала.
При
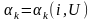 цепь называется нелинейной
электрической цепью (НЭЦ). Она
состоит из нелинейных R(i),
L(i)
и C(u).
Для НЭЦ принцип суперпозиции не
справедлив. В спектре сигнала, прошедшего
через НЭЦ, возникают новые частоты, не
содержащиеся в спектре входного сигнала.
цепь называется нелинейной
электрической цепью (НЭЦ). Она
состоит из нелинейных R(i),
L(i)
и C(u).
Для НЭЦ принцип суперпозиции не
справедлив. В спектре сигнала, прошедшего
через НЭЦ, возникают новые частоты, не
содержащиеся в спектре входного сигнала.
При
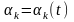 цепь называется
параметрической
(ПЭЦ) и
состоит из элементов, характеристики
(параметры) которых зависят от времени.
Для ПЭЦ справедлив принцип суперпозиции,
а в спектре выходного сигнала возможно
появление новых частот. Основу ПЭЦ
составляют нелинейные элементы, параметры
которых могут изменяться во времени
под воздействием управляющих напряжений
или токов.
цепь называется
параметрической
(ПЭЦ) и
состоит из элементов, характеристики
(параметры) которых зависят от времени.
Для ПЭЦ справедлив принцип суперпозиции,
а в спектре выходного сигнала возможно
появление новых частот. Основу ПЭЦ
составляют нелинейные элементы, параметры
которых могут изменяться во времени
под воздействием управляющих напряжений
или токов.
3.1.2 Аппроксимация нелинейных характеристик
Для анализа и расчета НЭЦ необходимо задать вольт-амперные (ВАХ) или иные аналогичные характеристики нелинейных элементов (НЭ) в аналитической форме. Реальные характеристики обычно имеют сложный вид, затрудняющий точное их описание с помощью достаточно простого аналитического выражения. Поэтому в этих случаях применяют различные способы аппроксимации характеристик, т. е. их представления относительно простыми функциями, приближенно отображающими истинные характеристики.
Выбор оптимальной аппроксимации зависит от вида нелинейной характеристики, а также от режима работы НЭ. Одним из наиболее распространенных способов аппроксимации является аппроксимация степенным полиномом, основанная на разложении нелинейной ВАХ i(u) в ряд Тейлора, сходящийся в окрестностях рабочей точки U0:
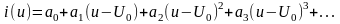 , (3.1.2)
, (3.1.2)
где коэффициенты ai, i = 1, …, n определяются выражением:
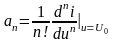 .
(3.1.3)
.
(3.1.3)
Коэффициент a1 представляет собой крутизну характеристики в рабочей точке и = U0, a2 – первую производную крутизны (с коэффициентом 1/2!), а3 – вторую производную крутизны (с коэффициентом 1/3!) и т. д. При заданной форме ВАХ величины коэффициентов ai, i = 1, …, n существенно зависят от положения рабочей точки Uo нa характеристике. Количество членов разложения n зависит от заданной точности расчётов.
Степенную аппроксимацию используют при анализе работы нелинейных цепей при воздействии относительно малых внешних воздействий.
При больших
амплитудах сигнала используют
кусочно-линейную аппроксимацию
нелинейной характеристики. Данный
способ основан на приближённой замене
реальной характеристики отрезками
прямых линий с различными наклонами.
Аппроксимация определяется двумя
параметрами – напряжением начала
характеристики
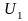 и крутизной S, имеющей
размерность проводимости. Математическая
форма аппроксимированной ВАХ имеет
вид:
и крутизной S, имеющей
размерность проводимости. Математическая
форма аппроксимированной ВАХ имеет
вид:
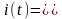 (3.1.4)
(3.1.4)
где – так называемое напряжение отсечки.
3.1.3 Усиление гармонических колебаний
Режим работы усилителей с нелинейной ВАХ в зависимости от напряжения входного сигнала можно условно разделить на квазилинейный (режим слабых сигналов) и нелинейный (режим сильных сигналов).
Н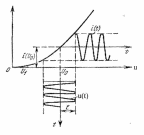
i
а рис. 3.1.1 представлен первый режим работы, при котором напряжение входного сигнала u(t) не выходит за пределы точки U1 и ВАХ i(u) удовлетворительно аппроксимируется степенным полиномом (3.1.2).Рисунок 3.1.1 – Слабо-нелинейный режим работы усилителя
Подставив в (3.1.2)
и(t) = Ecos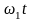 ,
получим:
,
получим:
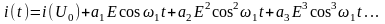 . (3.1.5)
. (3.1.5)
С помощью тригонометрических соотношений:
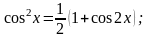
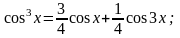
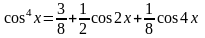 и
т.д., последнее выражение (3.1.5) приводится
к виду:
и
т.д., последнее выражение (3.1.5) приводится
к виду:
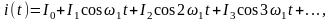 (3.1.6)
(3.1.6)
где
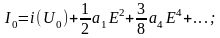
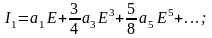
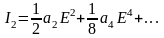 и
т.д. – соответственно амплитуда постоянной
составляющей и гармоник основной
частоты.
и
т.д. – соответственно амплитуда постоянной
составляющей и гармоник основной
частоты.
Из этого выражения видны последствия нелинейности ВАХ при усилении гармонического сигнала:
- амплитуда I1
первой гармоники (основной частоты
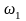 )
связана с амплитудой входного сигнала
Е нелинейным соотношением,
обусловленным нечётными степенями
аппроксимирующего ВАХ полинома (3.1.2):
)
связана с амплитудой входного сигнала
Е нелинейным соотношением,
обусловленным нечётными степенями
аппроксимирующего ВАХ полинома (3.1.2):
- ток i(t)
содержит высшие гармоники с частотами
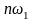 ,
кратными основной частоте
.
Чётные гармоники (с частотами 2ω1,
4ω1,…) обусловлены чётными
степенями, а нечётные гармоники (с
частотами 3ω1, 5ω1,…)
– нечётными степенями полинома.
,
кратными основной частоте
.
Чётные гармоники (с частотами 2ω1,
4ω1,…) обусловлены чётными
степенями, а нечётные гармоники (с
частотами 3ω1, 5ω1,…)
– нечётными степенями полинома.
Р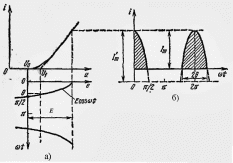 абота
усилителя во втором (нелинейном) режиме
характеризуется большой амплитудой
входного сигнала Е, сдвигом рабочей
точки
абота
усилителя во втором (нелинейном) режиме
характеризуется большой амплитудой
входного сигнала Е, сдвигом рабочей
точки
 влево и кусочно-линейной аппроксимацией
ВАХ (рис. 3.1.2, а).
влево и кусочно-линейной аппроксимацией
ВАХ (рис. 3.1.2, а).
Рисунок 3.1.2 – Нелинейный режим работы усилителя
При гармоническом
входном сигнале ток i(t)
приобретает импульсную форму (рис.
3.1.2, б). Угол
 ,
соответствующий изменению тока от
максимального значения Iт
до нуля, называется углом
отсечки тока. Длительность импульсов
тока равна 2
(рис. 3.1.2, б). Из рис. 3.1.2, а следует
выражение:
,
соответствующий изменению тока от
максимального значения Iт
до нуля, называется углом
отсечки тока. Длительность импульсов
тока равна 2
(рис. 3.1.2, б). Из рис. 3.1.2, а следует
выражение:
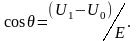 (3.1.7)
(3.1.7)
Амплитуды постоянной составляющей и гармоник определяются соответствующими коэффициентами ряда Фурье. Общее выражение для амплитуды n-ой гармоники имеет вид:
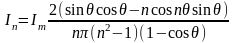 .
(3.1.8)
.
(3.1.8)
Отношение
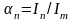 называется
коэффициентом n-ой (n
= 0, 1, 2, …) гармоники или коэффициентами
Берга.
называется
коэффициентом n-ой (n
= 0, 1, 2, …) гармоники или коэффициентами
Берга.
Графики зависимости
коэффициентов
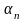 ,
а также отношения
,
а также отношения
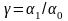 от угла отсечки
показаны на рис. 3.1.3. При
=
0 ток равен нулю (нелинейный элемент
заперт на протяжении всего периода);
при
= 180° отсечка тока отсутствует и режим
работы становится линейным.
от угла отсечки
показаны на рис. 3.1.3. При
=
0 ток равен нулю (нелинейный элемент
заперт на протяжении всего периода);
при
= 180° отсечка тока отсутствует и режим
работы становится линейным.
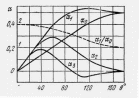

а) б)
Рисунок 3.1.3
– Графики зависимости коэффициентов
и
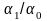 от угла отсечки
от угла отсечки
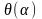 и спектры импульсов при различных
и спектры импульсов при различных
Из рассмотрения графиков и спектрограмм тока следует:
1) при работе с
углом отсечки меньше 180° отношение
амплитуды первой гармоники
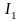 к постоянной составляющей
к постоянной составляющей
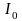 больше
единицы, между тем как в линейном режиме
это отношение не превышает единицы (при
больше
единицы, между тем как в линейном режиме
это отношение не превышает единицы (при
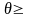 180°);
180°);
2) с уменьшением
отношение
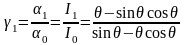 растёт;
растёт;
3) с повышением номера гармоники максимумы функций ап( ) перемещаются в область малых значений .
Все эти обстоятельства оказывают существенное влияние на выбор режима работы усилителя в зависимости от реализуемых им функций: усилении сигналов, умножении частоты и т.п.
Для максимизации
Iп надо при
заданном параметре SU1
найти такой оптимальный угол
отсечки
,
который максимизирует коэффициент
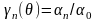 .
При Е = const
.
При Е = const
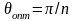 .
Оптимальными для умножения частоты в
2 и 3 раза являются углы отсечки
соответственно π/2 и π/3. Получить
существенное значение In
при п > 3 затруднительно,
поэтому для увеличения кратности
умножения частоты прибегают к
последовательному соединению отдельных
каскадов умножения.
.
Оптимальными для умножения частоты в
2 и 3 раза являются углы отсечки
соответственно π/2 и π/3. Получить
существенное значение In
при п > 3 затруднительно,
поэтому для увеличения кратности
умножения частоты прибегают к
последовательному соединению отдельных
каскадов умножения.
Для выходных
каскадов передатчика, где необходимо
обеспечить максимальный ток импульса
Iт, оптимальный
угол отсечки
определяется из условия максимизации
коэффициента
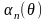 .
В этом случае для определения
.
В этом случае для определения
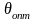 существует приближённая формула
существует приближённая формула
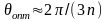 .
.
Уровень нелинейных искажений гармонического сигнала характеризуется коэффициентом гармоник, определяемым по формуле:
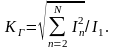 (3.1.9)
(3.1.9)
3.1.4 Преобразование частоты
Преобразованием частоты называется сдвиг спектра сигнала по оси частот на определённую постоянную величину при сохранении структуры сигнала.
При бигармоническом
воздействии
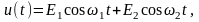 в составе тока появляются частоты
в составе тока появляются частоты
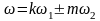 ,
,
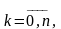
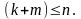 Гармоникам частоты
соответствуют значениям т = 0
(
Гармоникам частоты
соответствуют значениям т = 0
(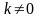 ),
гармоникам частоты
),
гармоникам частоты
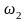 – значениям k = 0
(
– значениям k = 0
(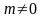 ).
Частоты, получаемые при значениях т
и k, не равных
нулю одновременно, называют
комбинационными. При этом число
(k + т) называют
порядком комбинационной частоты.
).
Частоты, получаемые при значениях т
и k, не равных
нулю одновременно, называют
комбинационными. При этом число
(k + т) называют
порядком комбинационной частоты.
Из качественного рассмотрения полученных результатов следует, что простой резистивный НЭ в сочетании с избирательной линейной цепью позволяет осуществить ряд преобразований, таких, как нелинейное резонансное усиление, умножение и преобразование частоты сигнала, выпрямление, детектирование модулированных сигналов, амплитудная модуляция, и др.
3.1.5 Нелинейное резонансное усиление
В радиопередающих устройствах широко применяются резонансные усилители мощности, отличительной особенностью которых является работа при больших амплитудах входных напряжений, т.е. на нелинейных участках ВАХ активных элементов, с отсечкой тока коллектора (рис. 3.1.4).
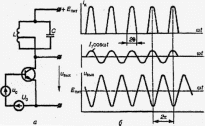
Рисунок 3.1.4 – Схема нелинейного резонансного усилителя (а) и временные диаграммы его работы (б)
Ток
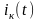 в выходной цепи усилителя при работе
с отсечкой имеет косинусоидальную
импульсную форму и содержит наряду с
постоянной составляющей и полезной
первой гармоникой ряд высших гармоник,
которые должны быть подавлены
(отфильтрованы). Эту задачу решает
параллельный колебательный контур,
настроенный на частоту
входного колебания. Основное преимущество
нелинейного режима – относительно
высокий КПД, под которым понимается
отношение полезной активной мощности
в выходной цепи усилителя при работе
с отсечкой имеет косинусоидальную
импульсную форму и содержит наряду с
постоянной составляющей и полезной
первой гармоникой ряд высших гармоник,
которые должны быть подавлены
(отфильтрованы). Эту задачу решает
параллельный колебательный контур,
настроенный на частоту
входного колебания. Основное преимущество
нелинейного режима – относительно
высокий КПД, под которым понимается
отношение полезной активной мощности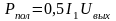 ,
выделяемой в резонансном контуре, к
мощности
,
выделяемой в резонансном контуре, к
мощности
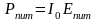 ,
потребляемой от источника питания:
,
потребляемой от источника питания:
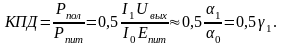
Анализ этого
выражения и графика (рис. 3.1.3, а)
показывает, что КПД максимально при
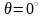 .
С ростом
КПД уменьшается и при
.
С ростом
КПД уменьшается и при
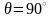 равно
равно
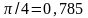 .
Поэтому, с точки зрения эффективности
использования источника питания, выгоден
режим с малым
,
когда КПД усилителя приближается к 1.
Однако при этом резко снижается
коэффициент
.
Поэтому, с точки зрения эффективности
использования источника питания, выгоден
режим с малым
,
когда КПД усилителя приближается к 1.
Однако при этом резко снижается
коэффициент
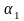 и для получения требуемой полезной
мощности приходится существенно
увеличивать амплитуду входного сигнала.
Принимая во внимание требование
линейности колебательной характеристики,
на практике идут на некоторое снижение
КПД и выбирают угол отсечки, близкий к
и для получения требуемой полезной
мощности приходится существенно
увеличивать амплитуду входного сигнала.
Принимая во внимание требование
линейности колебательной характеристики,
на практике идут на некоторое снижение
КПД и выбирают угол отсечки, близкий к
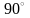 .
.
3.1.6 Параметрические цепи
Электрические цепи, в которых хотя бы один из параметров изменяется по какому-либо заданному закону, называются параметрическими (ПЦ). Предполагается, что изменение (модуляция) параметра или параметров осуществляется электронным способом при помощи управляющего колебания.
Важная роль ПЦ обусловлена их способностью преобразовывать спектры входных сигналов, а также возможностью создания малошумящих параметрических усилителей.
3.1.6.1 Преобразование частоты
Преобразователь
частоты состоит из смесителя –
параметрического безынерционного
элемента, и гетеродина – вспомогательного
генератора гармонических колебаний с
частотой
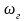 ,
служащего для параметрического управления
смесителем. Под действием напряжения
гетеродина дифференциальная крутизна
ВАХ смесителя периодически изменяется
во времени по закону:
,
служащего для параметрического управления
смесителем. Под действием напряжения
гетеродина дифференциальная крутизна
ВАХ смесителя периодически изменяется
во времени по закону:
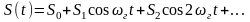 .
.
При воздействии
на вход смесителя сигнала с амплитудной
модуляцией (АМ)
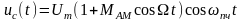 в выходном токе появляется составляющая:
в выходном токе появляется составляющая:
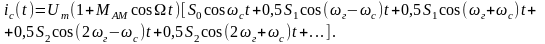
Ток на промежуточной
частоте
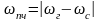 :
:
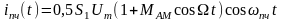
является АМ-сигналом с тем же законом, что и входной сигнал. Для выделения спектральных составляющих на промежуточной частоте в выходную цепь преобразователя включают полосовой фильтр, настроенный на промежуточную частоту.
3.1.6.2 Параметрическое усиление
Параметрическое усиление сигналов основано на особых свойствах параметрических реактивных элементов, которые в определённых условиях могут выступать в роли «посредников», передающих часть энергии от внешних управляющих источников (генератора накачки) к цепям, несущим полезный сигнал.
Рассмотрим
колебательный контур (рис. 3.1.5, а),
образованный постоянной индуктивностью
L, параметрической
ёмкостью С(t) и
сопротивлением потерь R,
в котором возбуждены собственные
колебания
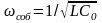 ,
где
,
где
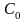 – среднее значение ёмкости.
– среднее значение ёмкости.
Дважды за период
собственных колебаний, в те моменты
времени, когда напряжение на конденсаторе
экстремально, его ёмкость скачком
уменьшается на величину
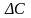 .
Возвращение в исходное состояние, т.е.
положительный перепад ёмкости, происходит
в момент времени, когда напряжение на
конденсаторе проходит через нуль (рис.
3.1.5, б). В связи с тем, что работа внешних
сил, выполняемая в моменты отрицательных
перепадов ёмкости, всегда положительна
независимо от знака напряжения на
обкладках, при такой накачке будет
наблюдаться однонаправленный приток
энергии в колебательный контур.
.
Возвращение в исходное состояние, т.е.
положительный перепад ёмкости, происходит
в момент времени, когда напряжение на
конденсаторе проходит через нуль (рис.
3.1.5, б). В связи с тем, что работа внешних
сил, выполняемая в моменты отрицательных
перепадов ёмкости, всегда положительна
независимо от знака напряжения на
обкладках, при такой накачке будет
наблюдаться однонаправленный приток
энергии в колебательный контур.
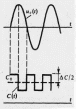
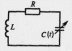
а) б)
Рисунок 3.1.5 –
Схема контура (а), графики входного
сигнала
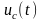 и
изменения ёмкости
и
изменения ёмкости
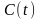 (б)
(б)
Возвращение ёмкости
в исходное состояние будет совершаться
в моменты времени, когда напряжение на
конденсаторе равно нулю, т.е. без затраты
энергии. Максимальная энергия, запасаемая
в конденсаторе, равна
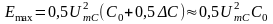 .
.
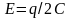 и
и
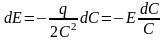 ,
следовательно, за период собственных
колебаний система получит энергию
накачки
,
следовательно, за период собственных
колебаний система получит энергию
накачки
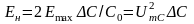 .
В то же время средняя мощность потерь
в контуре
.
В то же время средняя мощность потерь
в контуре
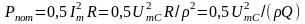 ,
где
,
где
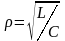 – характеристическое сопротивление,
– характеристическое сопротивление,
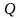 – добротность и
– добротность и
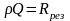 – активное резонансное сопротивление
контура. Энергия, рассеиваемая в резисторе
за период колебаний Т, равна
– активное резонансное сопротивление
контура. Энергия, рассеиваемая в резисторе
за период колебаний Т, равна
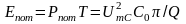 .
Если
.
Если
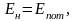 то за счёт действия источника накачки
происходит компенсация потерь в контуре.
Таким образом, регулируя относительную
величину
то за счёт действия источника накачки
происходит компенсация потерь в контуре.
Таким образом, регулируя относительную
величину
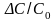 ,
т.е. глубину модуляции ёмкости, можно
осуществить как параметрическое усиление
сигнала, так и параметрическую генерацию.
,
т.е. глубину модуляции ёмкости, можно
осуществить как параметрическое усиление
сигнала, так и параметрическую генерацию.
Лекция 3.2 Формирование и детектирование сигналов амплитудной модуляции
В телекоммуникационных системах для передачи сообщений используется модуляция высокочастотных несущих, в качестве которых используется гармонический сигнал:
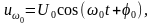
характеризующийся тремя параметрами: амплитудой U0, фазой φ0 и постоянной мгновенной частотой ω0. Изменяя эти параметры во времени по закону первичного сигнала b(t), получаем соответственно сигналы амплитудной (AM), фазовой (ФМ) и частотной (ЧМ) модуляции.
Зависимость меняющихся параметров несущей от первичного сигнала называют модуляционной характеристикой (МХ).
Система модуляции называется прямой, если модулированный сигнал u(t) в любой момент t зависит только от значения модулирующего сигнала b(t) в момент t. В этом случае b(t) входит непосредственно в выражение сигнала u(t). К прямым относятся AM, балансная (БАМ) и ФМ. Остальные системы модуляции, в которых u(t) зависит от общего поведения сигнала b(t), называются непрямыми. Среди них особый интерес представляют интегральные системы, в которых b(t) входит в выражение u(t) под интегралом.
Система модуляции называется линейной, если u(t) можно получить из b(t) с помощью линейных операций. Линейные системы могут быть прямыми (например, амплитудная – AM) и непрямыми (например, однополосная – ОМ).
3.2.1 Линейная амплитудная модуляция
Сигнал с линейной АМ описывается выражением:
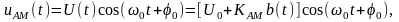 (3.2.1)
(3.2.1)
где U(t) ≥ 0 – огибающая AM сигнала; КАМ – крутизна характеристики модулятора, – амплитуда несущей частоты. Сигнал (3.2.1) можно записать в виде:
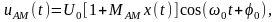 (3.2.2)
(3.2.2)
где
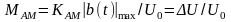 – коэффициент глубины амплитудной
модуляции,
– коэффициент глубины амплитудной
модуляции,
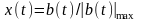 – нормированный модулирующий
(низкочастотный) сигнал, |х(t)|
≤ 1.
– нормированный модулирующий
(низкочастотный) сигнал, |х(t)|
≤ 1.
На
рис. 3.2.1, а
приведена векторная диаграмма AM
сигнала. Направление вектора неизменно,
а его длина меняется при изменении b(t).
При
гармоническом модулирующем сигнале
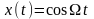 ,
где
,
где
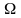 – модулирующая (низкая) частота, и
– модулирующая (низкая) частота, и
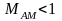 АМ сигнал:
АМ сигнал:
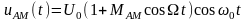 (3.2.2)
(3.2.2)
и
Um
меет вид, приведенный на рис. 3.2.1, б).
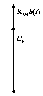
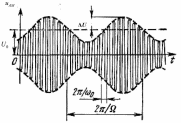
а) б)
Рисунок 3.2.1 – Векторная (а) и временная (б) диаграммы
АМ – сигнала
Раскрыв скобки в выражении (3.2.2) и представив произведение косинусов в виде косинуса суммы и разности углов, получим:
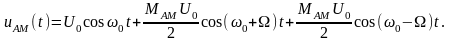 (3.2.3)
(3.2.3)
Этот сигнал содержит
три компоненты: на несущей частоте ω0
(первое слагаемое), на верхней боковой
частоте
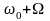 (второе слагаемое) и нижней боковой
частоте
(второе слагаемое) и нижней боковой
частоте
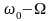 (третье слагаемое). Амплитудные
спектры (на положительных частотах)
первичного и AM сигнала
(3.2.3) приведены на рис. 3.2.2.
(третье слагаемое). Амплитудные
спектры (на положительных частотах)
первичного и AM сигнала
(3.2.3) приведены на рис. 3.2.2.
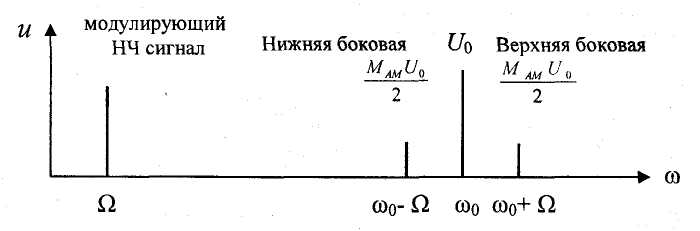
Рисунок 3.2.2 – Спектры гармонического модулирующего и АМ сигналов
Средняя за период
низкочастотного сигнала мощность
несущей в AM сигнале
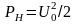 ,
а средняя мощность двух боковых частот
составляет
,
а средняя мощность двух боковых частот
составляет
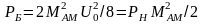 .
Суммарная средняя мощность
.
Суммарная средняя мощность
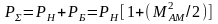 .
Полезная мощность AM
сигнала (определяемая боковыми
составляющими, дающими информацию о
первичном сигнале) составляет лишь
.
Полезная мощность AM
сигнала (определяемая боковыми
составляющими, дающими информацию о
первичном сигнале) составляет лишь
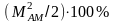 от мощности несущей и
от мощности несущей и
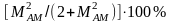 от общей средней мощности. При
от общей средней мощности. При
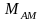 =
1 эти доли составляют соответственно
50 и 33 % (по 16,5% на каждую боковую). На
практике (во избежание перемодуляции
и для уменьшения искажений при модуляции
и детектировании)
=
1 эти доли составляют соответственно
50 и 33 % (по 16,5% на каждую боковую). На
практике (во избежание перемодуляции
и для уменьшения искажений при модуляции
и детектировании)
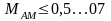 .
.
На рис. 3.2.3 даны
амплитудные спектры первичного и AM
сигналов при условии, что спектр b(t)
содержит составляющие от
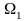 до
до
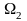 .
Спектр верхней боковой полосы (ВБП)
является масштабной копией спектра
модулирующего сигнала, сдвинутой в
область высоких частот на величину
.
Спектр нижней боковой полосы (НБП) также
повторяет спектр сигнала b(t),
но располагается зеркально относительно
несущей частоты
.
Ширина спектра АМ-сигнала равна
удвоенному значению наивысшей частоты
FB
в спектре модулирующего низкочастотного
сигнала, т.е.
.
Спектр верхней боковой полосы (ВБП)
является масштабной копией спектра
модулирующего сигнала, сдвинутой в
область высоких частот на величину
.
Спектр нижней боковой полосы (НБП) также
повторяет спектр сигнала b(t),
но располагается зеркально относительно
несущей частоты
.
Ширина спектра АМ-сигнала равна
удвоенному значению наивысшей частоты
FB
в спектре модулирующего низкочастотного
сигнала, т.е.
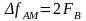 (для
приведённого на рис. 3.2.3 случая
(для
приведённого на рис. 3.2.3 случая
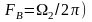 .
.

со сплошным спектром
3.2.2 Использование параметрических элементов для амплитудной модуляции и детектирования
Реализацию AM
можно рассматривать как частный случай
операции преобразования частоты. При
рассмотрении параметрической реализации
преобразования частоты можно исходить
из схемы перемножителя (рис. 3.2.5), взяв
в качестве входного сигнал с АМ по закону
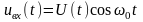 ,
а в качестве управляющего – гармонический
сигнал
,
а в качестве управляющего – гармонический
сигнал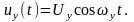
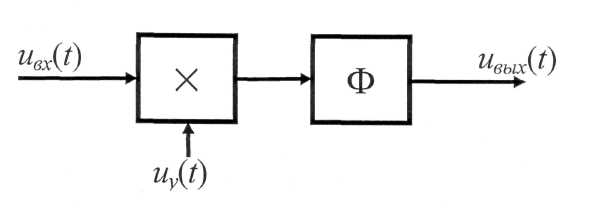
Рисунок 3.2.5 – Схема перемножения двух сигналов
Сигнал на выходе перемножителя равен:
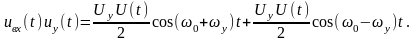
Фильтр (Ф) на выходе перемножителя пропускает с одинаковым коэффициентом передачи K лишь одно из слагаемых: при преобразовании вверх выходным сигналом является первое слагаемое, а при преобразовании вниз – второе слагаемое:
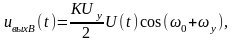
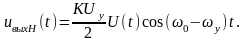
При преобразовании частоты (вверх или вниз) выходной сигнал пропорционален амплитуде входного сигнала и сигнала управления. Формы сигналов на входе и выходе параметрического преобразователя частоты совпадают.
Преобразователи частоты (перемножители двух функций) используют в приёмных и передающих устройствах при формировании и обработке сигналов АМ, ЧМ и ФМ.
Схема (3.2.5) может
быть использована для детектирования
АМ сигналов. Метод детектирования
посредством перемножения принимаемого
и опорного (управляющего) сигналов
называют когерентным, поскольку
предполагается знание в месте приёма
как частоты ω0 используемой
несущей, так и фазы, вносимой каналом
 в передаваемый сигнал s(t).
Детектор при этом называют синхронным.
Результат синхронного детектирования
существенно зависит от погрешности
фазирования ∆θ передатчика и
приёмника. Если опорный сигнал на приёме
в передаваемый сигнал s(t).
Детектор при этом называют синхронным.
Результат синхронного детектирования
существенно зависит от погрешности
фазирования ∆θ передатчика и
приёмника. Если опорный сигнал на приёме
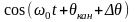 ,
то сигнал на выходе ФНЧ
,
то сигнал на выходе ФНЧ
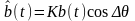 ,
где K – константа.
При
,
где K – константа.
При
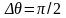 выходной результат равен нулю. Знание
в месте приёма параметров ω0
и
обеспечивается специальным устройством
их оценивания, входящим в общую систему
синхронизации работы передающего и
приёмного устройств.
выходной результат равен нулю. Знание
в месте приёма параметров ω0
и
обеспечивается специальным устройством
их оценивания, входящим в общую систему
синхронизации работы передающего и
приёмного устройств.
3.2.3 Использование нелинейных элементов для амплитудной модуляции и детектирования
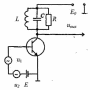 На
рис. 3.2.6 приведена однотактная схема
преобразования частоты на базе биполярного
п-р-п транзистора.
На
рис. 3.2.6 приведена однотактная схема
преобразования частоты на базе биполярного
п-р-п транзистора.
Рисунок 3.2.6 – Однотактная нелинейная схема преобразования частоты
При АМ
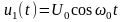 – сигнал несущей,
– сигнал несущей,
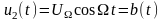 – первичный сигнал. Пользуясь
полиномиальной аппроксимацией для
характеристики iк
= f(ибэ), можно
написать:
– первичный сигнал. Пользуясь
полиномиальной аппроксимацией для
характеристики iк
= f(ибэ), можно
написать:
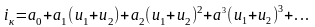 .
(3.2.4)
.
(3.2.4)
Резонансный контур в коллекторной цепи выделяет полезные продукты преобразования частоты (АМ). Если удовлетворительная аппроксимация характеристики iк = f(ибэ) возможна лишь полиномом выше второй степени, то на выходе нелинейной схемы появятся составляющие тока, приводящие к искажениям, которые оцениваются коэффициентом нелинейных искажений Kни (отношение амплитуд составляющих высших гармоник к первой гармонике).
3.2.4 Амплитудная модуляция без несущей
Линейная АМ обладает рядом существенных недостатков: во-первых, имеет низкие энергетические характеристики, а, во-вторых, ширина спектра АМ сигнала в 2 раза превышает ширину спектра модулирующего сигнала. По этим причинам на практике применяют более эффективные методы модуляции: АМ с подавленной несущей частотой (АМ-ПН) или балансной АМ (БАМ), а также однополосную модуляцию (ОМ или ОБП).
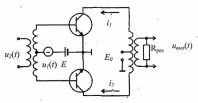 АМ-ПН
или БАМ можно реализовать в двухтактной
нелинейной схеме преобразования
частоты, показанной на рис. 3.2.7.
АМ-ПН
или БАМ можно реализовать в двухтактной
нелинейной схеме преобразования
частоты, показанной на рис. 3.2.7.
Рисунок 3.2.7 – Двухтактная нелинейная схема преобразования
частоты
В этой схеме благодаря трансформатору со средней точкой напряжение и2(t) поступает на базы двух транзисторов в противофазе, напряжение же и1(t) поступает на базы транзисторов в фазе. При аппроксимации нелинейной характеристики полиномом третьей степени токи в верхнем i1 и нижнем i2 транзисторах при одинаковых параметрах двух плеч (балансе) определяется формулой:
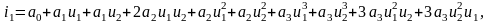
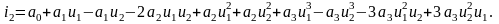 Выходное
напряжение пропорционально разностному
току:
Выходное
напряжение пропорционально разностному
току:
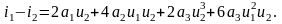 (3.2.6)
(3.2.6)
Для первой гармоники несущей в составе тока (3.2.6) получаем:
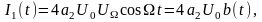
что соответствует неискажённой балансной модуляции.
3.2.5 Однополосная модуляция
В спектре ОМ сигнала присутствует только одна из боковых полос (ВБП или НБП). Ширина спектра частот ОМ сигнала равна ширине спектра частот первичного сигнала FВ, т.е. в 2 раза уже, чем AM сигнала.
ОМ сигналы по внешним характеристикам напоминают обычные АМ сигналы. ОМ сигнал можно получить из сигнала AM путём выделения (фильтрации) одной из боковых полос частот. Сигнал ОМ можно представить в виде:
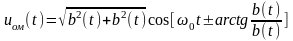 ,
(3.2.7)
,
(3.2.7)
где
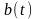 – функция, сопряжённая по Гильберту
функции
,
т.е. его можно рассматривать как сигнал
с амплитудно-фазовой модуляцией, в
котором амплитуда изменяется по закону
– функция, сопряжённая по Гильберту
функции
,
т.е. его можно рассматривать как сигнал
с амплитудно-фазовой модуляцией, в
котором амплитуда изменяется по закону
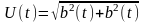 ,
а фаза – по закону
,
а фаза – по закону
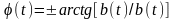 .
.
3.2.6 Нелинейное (некогерентное) детектирование АМ-сигналов
Этот метод
детектирования не требует знания фазы
.
На рис. 3.2.8 представлена схема однотактного
коллекторного детектора. Для того чтобы
нагрузка в коллекторной цепи выполняла
роль ФНЧ (для выделения полезного
продукта детектирования), должны
выполняться условия
 и
и
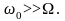 .
При этом для полезного сигнала с низкой
частотой
сопротивление нагрузки практически
равно R, а для
высокочастотных компонент оно близко
к нулю.
.
При этом для полезного сигнала с низкой
частотой
сопротивление нагрузки практически
равно R, а для
высокочастотных компонент оно близко
к нулю.
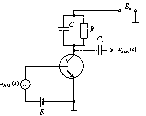
Рисунок 3.2.8 – Схема нелинейного (некогерентного) детектора
АМ-сигнала
За счёт додетекторного
усиления AM сигнал в цепи
базы достаточно интенсивен для того,
чтобы можно было использовать
кусочно-линейную аппроксимацию ВАХ iк
= f(ибэ) при
напряжении смещения, равным напряжению
отсечки Е =
.
Тогда угол отсечки
=
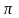 /2
независимо от изменения во времени
амплитуды AM сигнала
U(t)cos(
/2
независимо от изменения во времени
амплитуды AM сигнала
U(t)cos(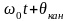 )
в цепи базы (
)
в цепи базы (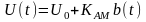 ).
Ток постоянной составляющей в цепи
коллектора равен:
).
Ток постоянной составляющей в цепи
коллектора равен:
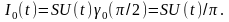
Напряжение на
нагрузке коллекторной цепи равно
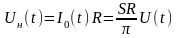 .
Зависимость полезного сигнала на выходе
детектора от модулированного сообщением
параметра несущей называют характеристикой
детектирования. В данном случае
– она линейная, а коэффициент передачи
детектора (отношение выходного напряжения
к амплитуде входного)
.
Зависимость полезного сигнала на выходе
детектора от модулированного сообщением
параметра несущей называют характеристикой
детектирования. В данном случае
– она линейная, а коэффициент передачи
детектора (отношение выходного напряжения
к амплитуде входного)
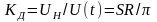 .
Полезный сигнал на выходе детектора
повторяет форму амплитуды входного
сигнала. Такой детектор называют
линейным, он не вносит искажений
в передаваемое сообщение. Напряжение
на выходе разделительной ёмкости Ср
(рис. 3.2.8) равно:
.
Полезный сигнал на выходе детектора
повторяет форму амплитуды входного
сигнала. Такой детектор называют
линейным, он не вносит искажений
в передаваемое сообщение. Напряжение
на выходе разделительной ёмкости Ср
(рис. 3.2.8) равно:
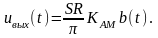
Если на вход
рассмотренного линейного детектора
подать AM-ПН сигнал, то
выходной сигнал не будет воспроизводить
форму первичного сигнала. Во избежание
искажений при детектировании АМ-ПН
сигнала надо в цепь базы схемы рис. 3.2.8
включить помимо напряжения смещения Е
ещё два источника: принимаемого
сигнала БАМ и восстановленного сигнала
несущей
 .
.
Лекция 3.3 Формирование и детектирование сигналов угловой модуляции
3.3.1 Свойства и характеристики сигналов угловой модуляции в частотной и временной областях
Модулированные сигналы, получаемые в результате изменения по закону первичного сигнала b(t) частоты или фазы несущей:
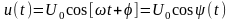 ,
(3.3.1)
,
(3.3.1)
называются сигналами
с угловой модуляцией (УМ).
Аргумент несущей частоты
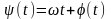 – полная фаза сигнала определяет
текущее значение фазового угла. Амплитуда
сигнала УМ и его средняя мощность
остаются неизменными.
– полная фаза сигнала определяет
текущее значение фазового угла. Амплитуда
сигнала УМ и его средняя мощность
остаются неизменными.
На практике различают два вида УМ: фазовая модуляция (ФМ) и частотная модуляция (ЧМ). Основные математические выражения для сигналов ЧМ и ФМ представлены в таблице 3.3.1.
Таблица 3.3.1 – Математические выражения для ЧМ и ФМ

Как
следует из последних выражений,
представленных в таблице 3.3.1, при
элементарном первичном сигнале
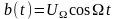 и постоянной частоте
сигналы ЧМ и ФМ практически не различимы.
В сигнал
и постоянной частоте
сигналы ЧМ и ФМ практически не различимы.
В сигнал
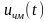 входит
интеграл первичного сигнала
входит
интеграл первичного сигнала
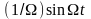 ,
а в
,
а в
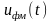 – сама функция
– сама функция
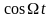 .
.
Графики зависимостей
девиации частоты
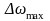 и фазы
и фазы
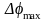 от частоты модулирующего сигнала Ω
представлены на рис. 3.3.1.
от частоты модулирующего сигнала Ω
представлены на рис. 3.3.1.
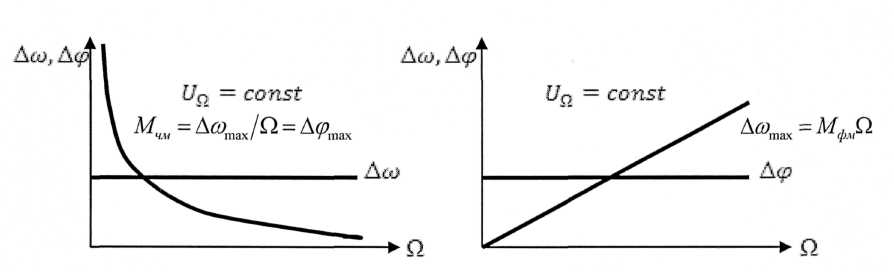
Рисунок 3.3.1 –
Графики зависимости
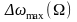 и
и
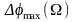
для сигналов с ЧМ (а) и ФМ (б)
Сигнал с УМ гармоническим сигналом можно представить в виде суммы гармонических колебаний:
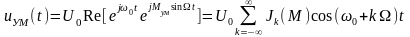 ,
(3.3.2)
,
(3.3.2)
г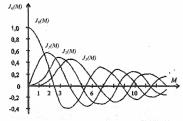 де
Jk(M)
–функция Бесселя k-го
порядка от аргумента М (М – любое
вещественное число). На рис. 3.3.2
показаны графики функции Бесселя
де
Jk(M)
–функция Бесселя k-го
порядка от аргумента М (М – любое
вещественное число). На рис. 3.3.2
показаны графики функции Бесселя
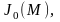
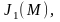
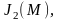
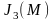 при положительном аргументе М.
Справедливо соотношение
при положительном аргументе М.
Справедливо соотношение .
.
Рисунок 3.3.2 – Графики функций Бесселя
Обычно считают, что можно пренебречь спектральными составляющими с номером k > (М+1), т. е. ширина спектра при тональной УМ равна:
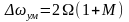 или
или
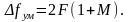 (4.3.3)
(4.3.3)
На рис. 3.3.3 показан амплитудный спектр сигнала (3.3.2) на положительных частотах при некотором значении М и = 1. Практическая ширина полосы частот при УМ в М + 1 раз шире, чем при AM.
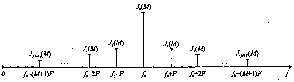
Рисунок 3.3.3 – Амплитудный спектр при УМ моногармоническим сигналом (на положительных частотах)
Для узкополосной
УМ (М << 1)
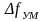 = 2F и в спектре
сигнала имеется только несущая и две
боковые составляющие (как при AM).
Этот результат, с учетом
,
следует из общей формулы (3.3.2) при М
<< 1 (при малых индексах J0(M)
≈1, J1(M)
= М/2, Jk(M)
= 0 при k ≥ 2):
= 2F и в спектре
сигнала имеется только несущая и две
боковые составляющие (как при AM).
Этот результат, с учетом
,
следует из общей формулы (3.3.2) при М
<< 1 (при малых индексах J0(M)
≈1, J1(M)
= М/2, Jk(M)
= 0 при k ≥ 2):
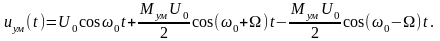
Для широкополосной УМ (М >> 1) из (3.3.3) имеем:
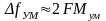 и
и
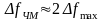 ,
(3.3.4)
,
(3.3.4)
т.е. ширина спектра при ЧМ равна удвоенной величине девиации частоты и не зависит от частоты модуляции F. Этот случай представляет основной практический интерес, так как при больших М помехоустойчивость УМ существенно выше, чем AM. Спектр УМ при негармоническом первичном сигнале определить трудно. Но он всегда сложнее, чем при AM при том же первичном сигнале b(t).
3.3.2 Методы формирования ЧМ и ФМ сигналов
На рис. 3.3.4 представлена схема получения ЧМ, основанная на изменении ёмкости (или индуктивности) контура, определяющего частоту генерации генератора гармонических колебаний, посредством присоединения к нему реактивного двухполюсника, управляемого первичным сигналом b(t).
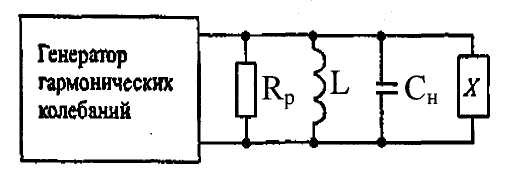
гармонических колебаний
Частота генерации
LC-генератора равна
резонансной частоте контура
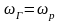 .
Резонансная частота ωр
меняется, если параллельно контуру
включить реактивное сопротивление X,
управляемое первичным сигналом b(t).
Проще всего реализуется параллельное
подключение к контуру управляемой
ёмкости С~[b(t)].
Достигается это при помощи варикапа
– управляемого полупроводникового
диода, работающего в запертом состоянии.
При параллельном подключении ёмкости
к контуру
.
Резонансная частота ωр
меняется, если параллельно контуру
включить реактивное сопротивление X,
управляемое первичным сигналом b(t).
Проще всего реализуется параллельное
подключение к контуру управляемой
ёмкости С~[b(t)].
Достигается это при помощи варикапа
– управляемого полупроводникового
диода, работающего в запертом состоянии.
При параллельном подключении ёмкости
к контуру
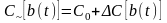 и его резонансная частота (а, следовательно,
и частота генерации) определяется
формулой:
и его резонансная частота (а, следовательно,
и частота генерации) определяется
формулой:
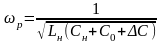 =
=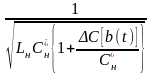 , (3.3.5)
, (3.3.5)
где
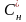 =
Сн + С0 –
суммарная начальная ёмкость контура.
=
Сн + С0 –
суммарная начальная ёмкость контура.
Построив зависимость
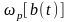 согласно этому выражению (рис. 3.3.5),
можно выбрать рабочий (линейный) участок
характеристики, на котором справедлива
аппроксимация:
согласно этому выражению (рис. 3.3.5),
можно выбрать рабочий (линейный) участок
характеристики, на котором справедлива
аппроксимация:
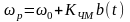 ,
(3.3.6)
,
(3.3.6)
где
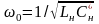 .
.
П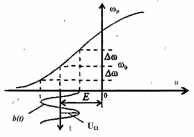 ри
гармоническом модулирующем сигнале
ри
гармоническом модулирующем сигнале
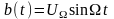 имеем
имеем
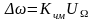 .
Максимально допустимые значения UΩ
(следовательно, и максимально
допустимые значения ∆ω) определяются
протяжённостью линейного участка кривой
.
Для увеличения девиации частоты
пользуются умножением частоты.
.
Максимально допустимые значения UΩ
(следовательно, и максимально
допустимые значения ∆ω) определяются
протяжённостью линейного участка кривой
.
Для увеличения девиации частоты
пользуются умножением частоты.
Рисунок 3.3.5 – Зависимость резонансной частоты контура
от сигнала b(t)
Эта схема может
использоваться и для получения ФМ, если
управление варикапом осуществляется
сигналом
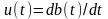 .
Тогда мгновенная резонансная частота
генератора меняется по закону
.
Тогда мгновенная резонансная частота
генератора меняется по закону
 ,
где k – константа.
Мгновенная фаза колебания
,
где k – константа.
Мгновенная фаза колебания что соответствует ФМ.
что соответствует ФМ.
3.3.3 Методы детектирования сигналов УМ
3.3.3.1 Синхронное (параметрическое) детектирование
На входы перемножителя
(рис. 3.3.6) поступает входной сигнал
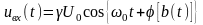 (
(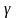 –коэффициент
передачи канала связи) и опорное колебание
–коэффициент
передачи канала связи) и опорное колебание
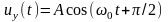 .
Выходной сигнал (после ФНЧ с коэффициентом
передачи K) равен:
.
Выходной сигнал (после ФНЧ с коэффициентом
передачи K) равен:
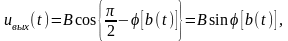
где
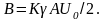
Если
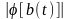 мало, то
мало, то
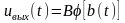 .
Следовательно, обеспечено неискаженное
детектирование фазы. При детектировании
ЧМ сигнала, поскольку
.
Следовательно, обеспечено неискаженное
детектирование фазы. При детектировании
ЧМ сигнала, поскольку
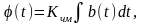 схема синхронного детектора должна
быть дополнена блоком дифференцирования.
схема синхронного детектора должна
быть дополнена блоком дифференцирования.
Рисунок 3.3.6 – Схема синхронного детектора
3.3.3.2 Нелинейные схемы детектирования
Одной из разновидностей
нелинейных схем детектирования при УМ
является фазовый детектор. Он может
быть построен по схеме нелинейного
детектора АМ сигналов с тремя источниками
в цепи базы (смещения Е, сигнала
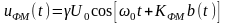 и опорного колебания
и опорного колебания
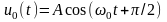 )
при условии, что характеристику
)
при условии, что характеристику
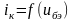 можно аппроксимировать квадратичной
зависимостью (рис. 3.3.7). Тогда:
можно аппроксимировать квадратичной
зависимостью (рис. 3.3.7). Тогда:
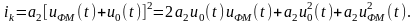
Полезный продукт на коллекторной нагрузке определяется первым слагаемым:
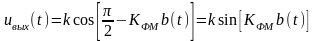 ,
,
г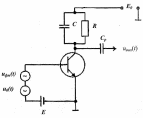 де
k – константа.
де
k – константа.
Рисунок 3.3.7 – Схема нелинейного фазового детектора
При малой девиации фазы (индексе модуляции) имеем:
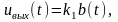
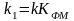 .
.
Если в цепь базы схемы рис. 3.3.7 подан вместо сигнала сигнал , то сигнал на коллекторной нагрузке необходимо продифференцировать.
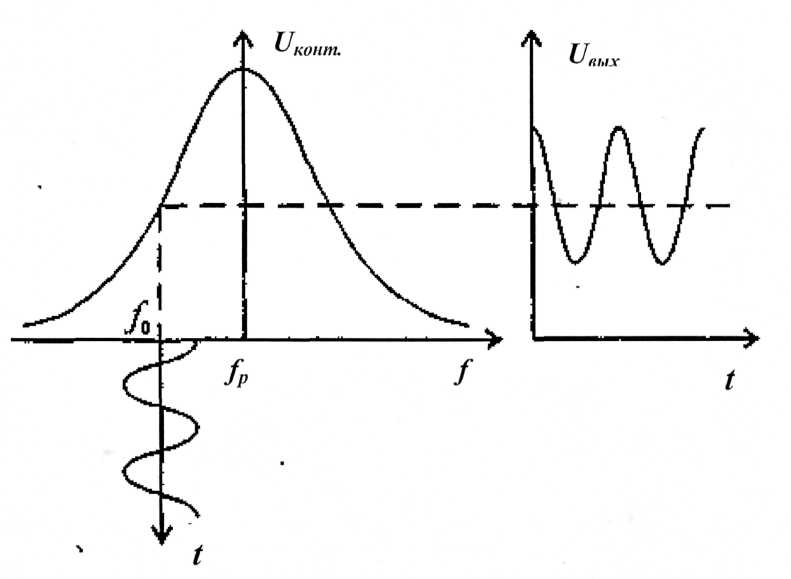 Другой
способ детектирования ЧМ сигнала основан
на его предварительном превращении
в сигнал амплитудно-частотной модуляции
(АЧМ) с помощью расстроенного
колебательного контура. Рисунок 3.3.8
иллюстрирует это преобразование.
Другой
способ детектирования ЧМ сигнала основан
на его предварительном превращении
в сигнал амплитудно-частотной модуляции
(АЧМ) с помощью расстроенного
колебательного контура. Рисунок 3.3.8
иллюстрирует это преобразование.
Рисунок 3.3.8 – Иллюстрация преобразования ЧМ в AM
Если точка f0 соответствует середине прямолинейного участка АЧХ колебательного контура и при качании частоты сигнал остаётся в пределах этого участка, то амплитуда полученного AM сигнала меняется пропорционально изменению частоты. Сигнал с выхода расстроенного колебательного контура подаётся на обычный амплитудный детектор.
Принципиальная схема частотного детектора (ЧД) с двумя расстроенными контурами приведена на рис. 3.3.9. Контура расстроены относительно средней частоты ЧМ сигнала 0, например: 1 0, 2 < 0. При чм(t) 0 она ближе к 1, чем к 2, амплитуда напряжения на входе Д1 больше, чем на на входе Д2, а напряжение в точке 1 больше чем в точке 2. При чм(t) < 0 напряжение в точке 2 больше, чем в точке 1. Полярность напряжения uнч(t) на выходе ЧД изменяется на противоположную.
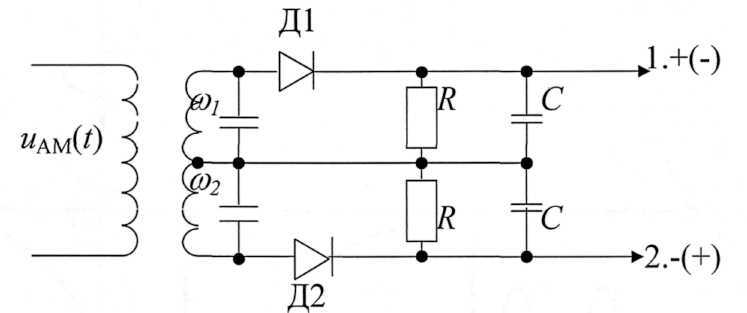
Рисунок 3.3.9 – Принципиальная схема ЧД с расстроенными
контурами
Зависимость постоянной составляющей тока в нагрузке детектора I0 от частоты входного сигнала I0 = f() называется статической характеристикой ЧД (рис. 3.3.10).
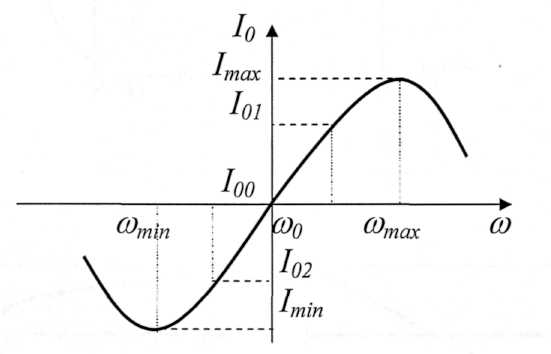
Рисунок 3.3.10 – Стандартный вид статической характеристики ЧД
Лекция 3.4 Формирование и детектирование сигналов, модулированных дискретными сообщениями. Понятие синхронизации и принципы ее обеспечения в системах электросвязи
В общем случае импульсная (дискретная, цифровая) модуляция – это процесс преобразования дискретных сигналов в сигналы, совместимые с характеристиками каналов. В импульсных системах радиосвязи применяют две ступени модуляции. Структурная схема системы связи для этого случая приведена на рис. 3.4.1.
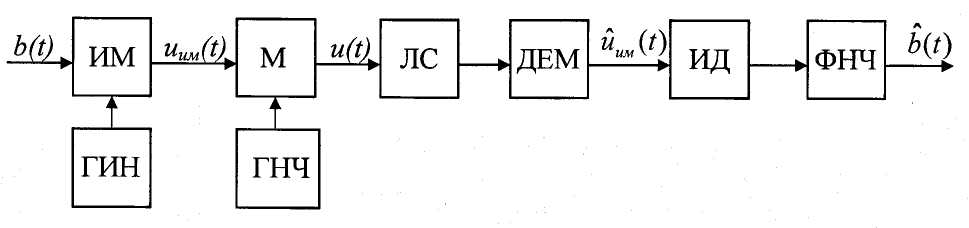
ИМ – импульсный
модулятор; ГИН – генератор импульсной
несущей; ГНЧ – генератор несущей частоты;
М – модулятор; ЛС – линия связи; ДЕМ –
демодулятор канального сигнала, выдающий
оценку сигнала ;
ИД – импульсный детектор;
–
оценка первичного сигнала, получаемая
на выходе ФНЧ.
;
ИД – импульсный детектор;
–
оценка первичного сигнала, получаемая
на выходе ФНЧ.
Рисунок 3.4.1 – Структурная схема двухступенчатой системы
передачи сообщений
На первой ступени осуществляется первичная импульсная (цифровая) модуляция. В качестве переносчиков информации («несущего колебания») на этой ступени используют импульсные последовательности. Для импульсной передачи сообщений по радиолиниям сигналом с выхода импульсного модулятора иим(t) осуществляется вторичная модуляция гармонической несущей.
3.4.1 Модуляция и детектирование импульсных переносчиков
В качестве
переносчика первичного сигнала b(t)
в импульсных системах связи используют
периодическую последовательность
видео- и радиоимпульсов. Периодическая
последовательность видеоимпульсов
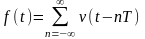 ,
где v(t)
– форма одиночного импульса, характеризуется
следующими параметрами: амплитудой h;
длительностью τи; частотой
следования Fи
= 1/Т (Т – период следования); положением
импульсов во времени относительно
тактовых точек. Изменяя один из
перечисленных параметров в соответствии
с изменением модулирующего сигнала
b(t),
можно получить четыре основных вида
импульсной модуляции (ИМ) видеоимпульсов:
амплитудно-импульсную модуляцию (АИМ),
модуляцию импульсов по длительности
или ширине (ДИМ или ШИМ), частотно-импульсную
модуляцию (ЧИМ), времяимпульсную модуляцию
(ВИМ). На рис. 3.4.2, а изображена периодическая
прямоугольная импульсная последовательность
f(t),
3.4.2, б – передаваемый первичный сигнал
b(t),
3.4.2 в, г, д, е – сигналы АИМ, ШИМ, ЧИМ,
ВИМ. Вертикальными штриховыми линиями
отмечены положения немодулированных
импульсов во времени (тактовые точки).
Предполагается, что при всех видах ИМ
изменения соответствующего параметра
пропорциональны значениям модулирующей
функции.
,
где v(t)
– форма одиночного импульса, характеризуется
следующими параметрами: амплитудой h;
длительностью τи; частотой
следования Fи
= 1/Т (Т – период следования); положением
импульсов во времени относительно
тактовых точек. Изменяя один из
перечисленных параметров в соответствии
с изменением модулирующего сигнала
b(t),
можно получить четыре основных вида
импульсной модуляции (ИМ) видеоимпульсов:
амплитудно-импульсную модуляцию (АИМ),
модуляцию импульсов по длительности
или ширине (ДИМ или ШИМ), частотно-импульсную
модуляцию (ЧИМ), времяимпульсную модуляцию
(ВИМ). На рис. 3.4.2, а изображена периодическая
прямоугольная импульсная последовательность
f(t),
3.4.2, б – передаваемый первичный сигнал
b(t),
3.4.2 в, г, д, е – сигналы АИМ, ШИМ, ЧИМ,
ВИМ. Вертикальными штриховыми линиями
отмечены положения немодулированных
импульсов во времени (тактовые точки).
Предполагается, что при всех видах ИМ
изменения соответствующего параметра
пропорциональны значениям модулирующей
функции.
Частота следования
импульсов Fи в
импульсных системах связи, как и частота
дискретизации fд,
определяются максимальной частотой
спектра первичного сигнала Fв:
Fи = fд
≥ 2Fв. Сигнал
АИМ определяетсявыражением
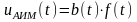 .
Спектр этого сигнала представляет
собой сумму спектров AM
сигналов на кратных гармониках kFи
спектра периодического импульсного
переносчика
.
Спектр этого сигнала представляет
собой сумму спектров AM
сигналов на кратных гармониках kFи
спектра периодического импульсного
переносчика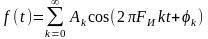 .
Спектр AM сигнала на
отдельной поднесущей kFи
находится аналогично тому, как это
осуществляется для аналоговых сигналов.
.
Спектр AM сигнала на
отдельной поднесущей kFи
находится аналогично тому, как это
осуществляется для аналоговых сигналов.
На рис. 3.4.3, б показан амплитудный спектр АИМ (на положительных частотах) при модуляции первичным сигналом со спектром, показанным на рис. 3.4.3, а. Из рис. 3.4.3, б следует метод детектирования АИМ сигнала: детектирование детектором AM сигналов можно вести на любой из поднесущих kFи (k = 0, 1, 2, ...). Проще всего выполнить детектирование посредством линейного ФНЧ, АЧХ которого изображена на рис. 3.4.3, б штриховой линией. Отфильтровка нежелательных частотных составляющих выполняется тем проще, чем лучше выполняется неравенство (Fи – Fв) > Fв или Fи > 2Fв (т.е. чем меньше интервал дискретизации первичного сигнала). Ограничив ширину спектра АИМ сигнала первым лепестком огибающей кривой на рис. 3.4.3, получаем:
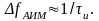 (3.4.1)
(3.4.1)
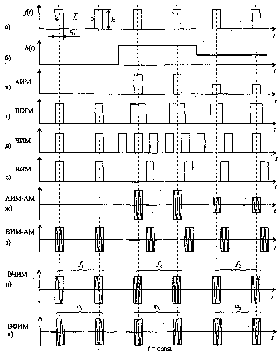
Рисунок 3.4.2 – Временные диаграммы различных видов
импульсной модуляции
Обычно скважность импульсов переносчика выбирают достаточно большой, т.е.:
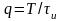 >> 1.
(3.4.2)
>> 1.
(3.4.2)
Большие временные интервалы между импульсами используют для передачи рабочих импульсов от других источников, т.е. для осуществления многоканальной передачи с временным разделением каналов. С учётом (3.4.1) и (3.4.2) следует:
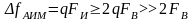 ,
,
т.е. сигнал при АИМ (это справедливо и при других видах ИМ) занимает значительно более широкую полосу частот, чем первичный сигнал b(t).

а )
)
 0
0 

б
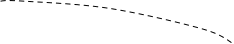 )
)


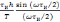
0
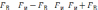
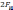
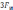
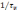 f
f
Рисунок 3.4.3 – Спектры первичного сигнала (а) и АИМ сигнала на
положительных частотах (б)
На рис. 3.4.2, ж показан сигнал АИМ после вторичной модуляции высокочастотной гармонической несущей по амплитуде. Такая двойная модуляция обозначается АИМ-АМ. На рис. 3.4.2, з показан сигнал ВИМ после вторичной модуляции гармонической несущей по амплитуде (ВИМ-АМ).
При использовании в качестве несущей периодической последовательности радиоимпульсов можно получить ещё два вида импульсной модуляции: высокочастотную импульсную модуляцию по частоте (ВЧИМ) и высокочастотную импульсную модуляцию по фазе (ВФИМ). Сигнал при этих видах модуляции показан на рис. 3.4.2, и и рис. 3.4.2, к. Сигнал ВИМ-АМ называют также сигналом высокочастотной временной импульсной модуляции (ВВИМ).
Детектирование сигналов ВИМ (или детектирование сигналов ВИМ-АМ на второй ступени демодуляции), которые часто используются на практике, можно проводить различными методами. Один из них – превращение ВИМ в АИМ. Для этого интегрирующее устройство включается при нулевых начальных условиях в тактовый интервал и выключается при появлении переднего фронта импульса сигнала ВИМ. Уровни сигнала на интеграторе определяют сигнал АИМ. Последний детектируется обычным образом.
3.4.2 Методы вторичной модуляции и демодуляции
Вторичная модуляция (манипуляция) – это процесс преобразования дискретного (цифрового) первичного сигнала в синусоидальный. Так же как и аналоговую цифровую модуляцию можно определить как процесс управления амплитудой, частотой или фазой радиочастотной несущей в соответствие с передаваемой информацией. Отсюда и основные типы манипуляции: амплитудная (АМн, ASK – amplitudeshiftkeying), частотная (ЧМн, FSK – frequencyshiftkeying) и фазовая (ФМн, PSK – phaseshiftkeying). В последнее время широкое применение находят комбинированные виды манипуляции – амплитудно-фазовая (АФМ, APK – amplitudephasekeying), квадратурная амплитудная (КАМ, QAM – quadratureamplitudemodulation), а также разновидности ФМн. Наиболее распространённые форматы цифровой манипуляции представлены в табл. 3.4.1.
В
общем случае при М-арной
передаче сигналов модулятор получает
k
исходных (канальных) битов и в каждый
тактовый интервал времени формирует
один из
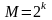 возможных
сигналов. Частным случаем М-уровней
манипуляции является бинарная с k
= 1.
возможных
сигналов. Частным случаем М-уровней
манипуляции является бинарная с k
= 1.
При ФМн, ЧМн
и АМн соответственно фаза
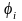 ,
частота
,
частота
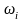 и амплитуда несущей (энергия сигнала
и амплитуда несущей (энергия сигнала
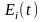 )
могут принимать М дискретных
значений; при АФМ М дискретных
значений могут принимать как амплитуда,
так и фаза несущей.
)
могут принимать М дискретных
значений; при АФМ М дискретных
значений могут принимать как амплитуда,
так и фаза несущей.
Таблица 4.4.1 – Форматы основных видов цифровой манипуляции
-
Аналитическое
представление
Временная
диаграмма сигнала
Векторная
диаграмма
а) ФМн (PSK)
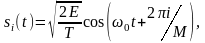
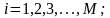
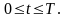
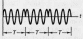
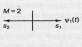
б) ЧМн (FSK)


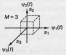
в) АМн (АSK)
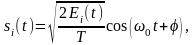
г) АФМ (APK)
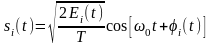 ,
,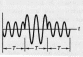

Е – энергия символа, T – длительность символа, M – количество сигналов (уровней манипуляции),
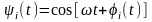 – фаза символа
– фаза символа
В приёмных устройствах цифровых систем связи в соответствии с двумя ступенями модуляции обратное преобразование сигналов осуществляется двухступенчатой системой демодуляции. На первой ступени осуществляется демодуляция (восстановление дискретного или цифрового сигнала), на второй – детектирование (принятие решения относительно символьного значения принятого сигнала). В зависимости от того, используется или нет информация о фазе несущей, приём сигналов называется когерентным или некогерентным. При идеальном когерентном приёме демодулятор перемножает и интегрирует входной сигнал с прототипами всех исходных сигналов (определяет корреляцию). Сигналы – прототипы дублируют алфавит всех передаваемых сигналов по всем параметрам, включая фазу несущей частоты. Не смотря на большую по сравнению с некогерентными сложность когерентных приёмников, они обеспечивают меньшую вероятность ошибки.
3.4.3 Синхронизация в системах электросвязи
Для нормального функционирования цифрового приёмника или демодулятора необходимо наличие некоторого уровня синхронизации сигнала. Например, при когерентной фазовой демодуляции приёмник должен генерировать опорные сигналы, фаза которых идентична фазе элементов сигнального алфавита передатчика. В процессе принятия решения относительно значения принятого символа (по принципу максимального правдоподобия) эти сигналы сравниваются с поступающими.
При генерации подобных опорных сигналов приёмник должен быть синхронизирован по несущей частоте, т.е. фаза принимаемой несущей частоты и её копии в приёмнике должны быть согласованы (необходимое условие когерентного детектирования). Этот процесс называется фазовой автоподстройкой частоты (ФАПЧ). В результате ФАПЧ гетеродин приёмника синхронизируется по частоте и фазе с принятым сигналом.
Приёмник должен точно знать также моменты времени начала и конца поступающих символов. Эта информация необходима для определения соответствующего интервала интегрирования символа (интервал накопления энергии перед принятием решения относительно значения символа). Если приёмник интегрирует по интервалу несоответствующей длины или по интервалу, захватывающему два символа, способность к принятию точного решения снижается.
Символьная (тактовая) и фазовая синхронизации необходимы для генерации в приёмнике копии переданного сигнала: для фазовой синхронизации – это точная копия несущей, для символьной – это импульсная последовательность, синхронизированная по скорости передачи символа.
Во многих системах связи требуется еще более высокий уровень синхронизации, который обычно называется кадровой (цикловой) синхронизацией. Кадровая синхронизация требуется при передаче сообщений блоками, содержащими фиксированное число символов (например, блочные помехоустойчивые коды, системы связи с временным разделением каналов). При блочном кодировании декодер должен знать расположение границ между кодовыми словами, что необходимо для верного декодирования сообщения. При использовании систем с временным разделением каналов (ВРК) нужно знать расположение границ между отдельными пользователями, что необходимо для верного направления информации. Кадровая синхронизация обеспечивается генерацией импульсной последовательности, синхронизированной по времени с моментами начала и конца кадра, а по скорости – со скоростью передачи кадров.
Большинство систем цифровой связи, использующих когерентную модуляцию, требуют всех трех уровней синхронизации: фазовой, символьной и кадровой. Системы с некогерентным приёмом точной синхронизации фазы не требуют, поэтому достаточно только символьной и кадровой синхронизации. Кроме того, некогерентным системам необходима частотная синхронизация. Частотная синхронизация отличается от фазовой тем, что копия несущей, генерируемая приёмником, может иметь произвольные сдвиги фазы относительно принятой несущей. Структура приёмника упрощается, если не предъявляются требования относительно определения точного значения фазы поступающей несущей. Однако, это упрощение влечет за собой ухудшение зависимости достоверности передачи от ОСШ.
Имеются два базовых подхода для обеспечения синхронизации по несущей частоте в приёмнике. Один сводится к замешиванию при передаче, обычно по частоте, специального сигнала, называемого пилот-сигналом, который можно извлечь из принимаемого сигнала и по его частоте и фазе синхронизировать местный генератор несущей приёмника. При одновременной передаче по каналу модулированной несущей (пилот-сигнала) и информационного сигнала, приёмник для захвата и отслеживания несущей частоты использует замкнутую петлю ФАПЧ. ФАПЧ имеет узкую полосу пропускания, вследствие чего она слабо подвержена воздействию частотных компонент и информационного сигнала.
Второй подход, более предпочтительный на практике, сводится к непосредственной оценке фазы несущей по модулированному сигналу. Этот подход имеет явное преимущество, поскольку вся мощность передатчика направлена на передачу информационного сигнала.
Выводы по теме 3
Все электрические цепи подразделяются на линейные (ЛЭЦ), нелинейные (НЭЦ) и параметрические (ПЭЦ). Для ЛЭЦ справедлив принцип суперпозиции, в спектре выходного сигналаотсутствуют новые частоты, отсутствующие в спектре входного сигнала. Для НЭЦ принцип суперпозиции не справедлив, в спектре выходного сигнала возникают новые частоты, не содержащиеся в спектре входного сигнала. Для ПЭЦ справедлив принцип суперпозиции, а в спектре выходного сигнала возможно появление новых частот.
Для аппроксимации реальных ВАХ безынерционных НЭЦ применяются различные функции простого вида. Наиболее распространены кусочно-линейная, степенная и показательная (экспоненциальная) аппроксимации.
Много преобразований сигналов в системах электрической связи (преобразование и умножение частоты, генерация колебаний, модуляция и демодуляция, выпрямление и др.) связано с трансформацией спектра, следовательно, они могут бытьвыполнены в НЭЦ или ПЭЦ.
Вследствие линейности амплитудной модуляции спектр AM сигнала повторяет форму спектра сообщения и занимает полосу, в два раза превышающую максимальную частоту спектра первичного (модулирующего) сигнала.
Из энергетических соображений и соображений экономии полосы частот канала представляют интерес системы с балансной модуляцией (АМ без несущей) или системы с одной боковой полосой (ОБП).
Фазовая и частотная модуляция является разновидностями угловой модуляции.
Спектр сигналов с УМ при больших индексах модуляции М шире и сложнее спектра AM.
Временные и спектральные характеристики цифрового первичного сигнала существенно зависят от выбора аналогового переносчика дискретных сообщений.
Модулированный сигнал при импульсном переносчике занимает более широкую полосу частот, чем при гармонической несущей.
Для нормального функционирования цифрового приёмника или демодулятора необходимо наличие синхронизации сигнала. Основными видами синхронизации являются: частотная и фазовая радиоприёмного устройства; символьная (тактовая) и кадровая (цикловая) демультиплексоров.
Контрольные вопросы по теме 3
1. Какая электрическая цепь называется линейной, нелинейной, параметрической?
2. Для каких цепей справедлив принцип суперпозиции?
3. На выходах каких цепей в спектрах сигналов появляются новые частоты?
4. Что такое аппроксимация?
5. Какие виды аппроксимации Вы знаете?
6. Что такое аппроксимация полиномом?
7. Назовите режимы работы усилителей с нелинейной ВАХ.
8. Поясните последствия нелинейности ВАХ при усилении гармонического сигнала.
9. Дайте определение угла отсечки тока.
10. Что такое оптимальный угол отсечки?
11. Что такое комбинационные частоты?
12. Запишите аналитическое выражение для АМ сигнала.
13. Нарисуйте временную диаграмму АМ сигнала при гармонической модуляции и при произвольном модулирующем сигнале.
14. Нарисуйте спектр АМ сигнала при гармонической модуляции и при произвольном спектре модулирующего сигнала.
15. Что такое глубина модуляции?
16. Нарисуйте принципиальную схему амплитудного модулятора.
17. Рассчитайте спектр тока на выходе модулятора и спектр напряжения на контуре модулятора.
28. Что такое СМХ?
19. Каковы энергетические показатели АМ?
В чём состоят преимущества и недостатки однополосной модуляции.
Запишите аналитические выражения для ЧМ и ФМ сигналов.
Что такое девиация частоты?
Чему равен индекс ЧМ?
Дайте определение девиации фазы и индекса ФМ.
Нарисуйте временную диаграмму ЧМ сигнала при гармонической модуляции.
Нарисуйте спектр ЧМ сигнала для очень малых и больших значений индекса ЧМ.
Нарисуйте принципиальную схему частотного модулятора.
Что такое СМХ частотного модулятора?
Нарисуйте принципиальную схему частотного детектора.
Что такое СХД?
Нарисуйте принципиальную схему синхронного детектора.
Назовите основные виды импульсной модуляции.
Нарисуйте спектрограмму АИМ сигнала на положительных частотах и прокомментируйте её.
Дайте определение вторичной модуляции и назовите основные её методы.
Для чего в цифровых приёмниках необходима синхронизация?
Назовите основные виды синхронизации и их назначение.
Список литературы по теме 3
1. Теория электрической связи: Учебник для вузов /Зюко А.Г., Кловский Д.Д., Коржик В.И., Назаров М.В. - М.: Радио и связь, 1999. - 432 с.
2. Гоноровский И.С. Радиотехнические цепи и сигналы. - М.: Радио и связь, 1986. - 512 с.
3. Баскаков С.И. Радиотехнические цепи и сигналы. Учебник для вузов. – М.: Высш. шк., 2005. – 462 с.
