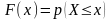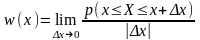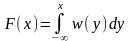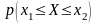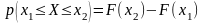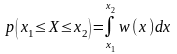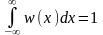- •Теория электрической связи
- •Часть 1
- •Тема 1 Общие сведения о системах и сетях электросвязи
- •Тема 2 Математические модели сигналов
- •Тема 3 Методы формирования и преобразования сигналов
- •Тема 4 Цифровая обработка сигналов
- •Тема 5 Математические модели каналов связи. Преобразование сигналов в каналах связи
Тема 2 Математические модели сигналов
Лекция 2.1 Математические модели детерминированных сигналов
2.1.1 Прямое и косвенное описание сигналов
В ТЭС применяют два основных способа представления сигналов: пространственно-временное и спектрально-частотное. В первом случае математической моделью сигнала может быть функциональная зависимость, аргументом которой является время. Во втором случае заданная функция времени (сигнал) представляется в виде суммы гармоник основной частоты, параметрами которых являются амплитуды и их фазы. Для определения этих параметров производится разложение исходной функции х(t) по базисным функциям.
Способы представления сигналов, являющихся реализациями как случайных, так и детерминированных процессов, подразделяются на прямые и косвенные.
К прямым способам описания относится аналитическое представление реализаций процесса временными функциями на основе функциональной связи значений сигнала в данный момент с его значениями в прошлом.
К косвенным способам относятся аналитические представления процессов производными функциями, полученными путём преобразования временных зависимостей процесса. Характерным примером косвенного описания процесса является его спектральное описание.
Косвенное описание процессов находит основное применение в задачах анализа, состоящих в получении косвенного описания системы при известном её прямом описании. Получение прямого описания системы по заданному косвенному является задачей синтеза. Последняя задача в общем случае не имеет однозначного решения.
2.1.2 Динамическое представление сигналов
Многие задачи, решаемые в процессе разработки, производства и эксплуатации систем связи, требуют специфической формы представления сигнала. При этом необходимо располагать информацией не только о мгновенных значениях сигнала, но и о его поведении на всей временной оси от «прошлого» до «будущего». В теории линейных электрических цепей изучаются методы определения откликов цепей на воздействие конкретных элементарных сигналов. В ТЭС приходится определять отклики различных систем на воздействие, в общем случае, сложных сигналов. В связи с этим представляет интерес представления сложных сигналов в виде суммы элементарных сигналов, реакция на которые исследуемой системы может быть получена относительно простым (известным) путём.
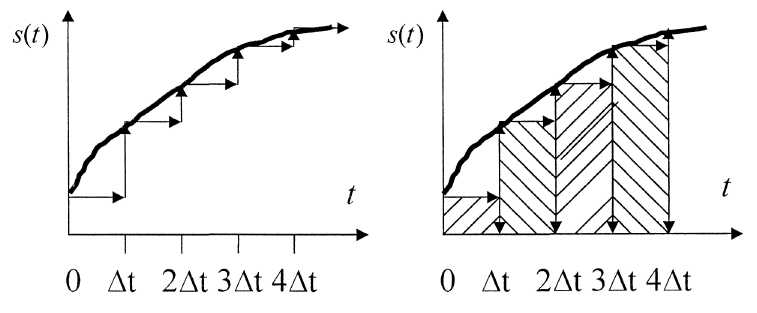
В динамических моделях реальный сигнал приближенно представляется суммой некоторых элементарных сигналов, возникающих в последовательные моменты времени. Устремив к нулю длительность отдельных элементарных сигналов, в пределе можно получить точное представление исходного сигнала. Такой способ описания сигналов называется динамическим представлением, подчеркивая этим развивающийся во времени характер процесса.
Существуют два способа динамического представления.
1) В качестве элементарных сигналов используются ступенчатые функции, возникающие через равные промежутки времени ∆t (рис. 2.1.1, а). Высота каждой ступеньки равна приращению сигнала на интервале времени ∆t.
2) Элементарными сигналами служат прямоугольные импульсы. Эти импульсы непосредственно примыкают друг к другу и образуют последовательность, вписанную в кривую или описанную вокруг нее (рис. 2.1.1, б).
Для динамического описания сигналов используются следующие виды элементарных функций:
- функция включения
(Хэвисайда)
 ;
;
- δ-функция (функция Дирака).
а) б)
Рисунок 2.1.1 – Способы динамического представления сигналов (стрелками показаны пути изменения во времени отдельных
элементарных слагаемых)
Формулы динамического представления произвольного сигнала посредством функций включения и δ-функций имеют вид:
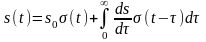 ,
,
где
 – начальное значение сигнала;
– начальное значение сигнала;
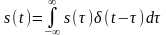 ,
,
т. е. интеграл по
времени произведения непрерывной
функции на
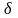 -
функцию равен значению непрерывной
функции в точке сосредоточения
–
импульса. Это свойство называется
фильтрующим свойством
-
функции.
-
функцию равен значению непрерывной
функции в точке сосредоточения
–
импульса. Это свойство называется
фильтрующим свойством
-
функции.
Физическая размерность - функции с-1.
2.1.3 Представление сигналов в метрических и топологических пространствах
Линейным или
векторным называется пространство
сигналов, для элементов которого
выполняются правила сложения и умножения
на любое число из некоторого множества{λ},
называемого множеством скаляров.
Сложение векторов производится
покоординатно, т.е.
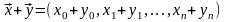 и принадлежит данному пространству,
а произведение
и принадлежит данному пространству,
а произведение
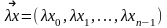 и также принадлежит данному
пространству. Операция суммирования
коммутативна
и также принадлежит данному
пространству. Операция суммирования
коммутативна
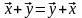 и ассоциативна
и ассоциативна
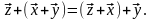 В линейном пространстве существует
нулевой элемент 0, такой, что
В линейном пространстве существует
нулевой элемент 0, такой, что
 + 0 =
и каждому элементу
соответствует противоположный
элемент
+ 0 =
и каждому элементу
соответствует противоположный
элемент
 ,
так что
+ (
)
= 0.
,
так что
+ (
)
= 0.
Вектор,
образованный суммированием п
линейно
независимых (базисных) векторов
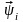 со скалярными коэффициентами хi
называется их линейной
комбинацией
=
со скалярными коэффициентами хi
называется их линейной
комбинацией
=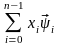 .
Множество векторов
.
Множество векторов
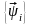 называется линейно
независимым (базисом),
если условие:
называется линейно
независимым (базисом),
если условие:
= 0 (2.1.4)
выполняется лишь тогда, когда все xi = 0, т. е. линейно независимым называется множество , для которого ни одна из его компонент не может быть образована линейной комбинацией других. Размерность линейного пространства определяется числом любых линейно независимых базисных векторов , образующих это пространство.
Система линейно независимых векторов образует координатный базис в линейном пространстве. Сигнал s(t) в таком базисе можно представить в виде:
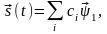
где числа {c1, c2 , …} – проекции сигнала s(t) относительно выбранного базиса.
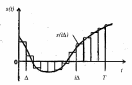 При
переходе к n-мерному
пространству некоторое приближённое
представление о сигнале s(t)
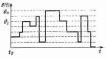
можно составить по её отображению
последовательностью прямоугольных
импульсов, имеющих на интервалах i∆t
значения s(i∆t)
(рис. 2.1.2).
При
переходе к n-мерному
пространству некоторое приближённое
представление о сигнале s(t)
можно составить по её отображению
последовательностью прямоугольных
импульсов, имеющих на интервалах i∆t
значения s(i∆t)
(рис. 2.1.2).
Рисунок 2.1.2 – Отображение непрерывной функции
последовательностью прямоугольных импульсов
При условном представлении функции s(t) на интервале (0; T) «вектором», для его определения потребуется п = Т/∆t координат si= s(i∆t), т. е.:
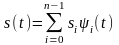 ,
(2.1.5)
,
(2.1.5)
где
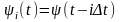 – элементарные базисные функции;
– элементарные базисные функции;
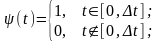
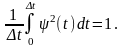
Вектор
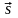 ,
соответствующий сигналу s(t),
в n-мерном пространстве
единичных ортов
,
соответствующий сигналу s(t),
в n-мерном пространстве
единичных ортов
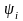 будет полностью определяться его
координатами
= (s0, s1,
…, sn-1).
будет полностью определяться его
координатами
= (s0, s1,
…, sn-1).
В векторном пространстве длина вектора называется его нормой. Нормированные пространства определяются заданием нормы || ||, удовлетворяющей следующим аксиомам:
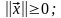
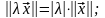
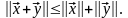
Вещественные аналоговые и комплексные сигналы имеют соответственно норму:
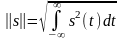 ,
(2.1.6)
,
(2.1.6)
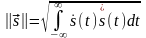 ,
(2.1.7)
,
(2.1.7)
где
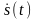 – комплексная, а
– комплексная, а
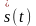 – комплексно-сопряженная функция.
– комплексно-сопряженная функция.
Квадрат нормы носит название энергии сигнала:
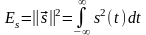 .
.
Эта энергия выделяется на резисторе с R = 1Ом при воздействии напряжения s(t).
Линейное пространство, в котором определено расстояние (метрика) между элементами (векторами) пространства, удовлетворяющее следующим правилам:
d(
,
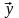 )
– вещественное неотрицательное число;
)
– вещественное неотрицательное число;
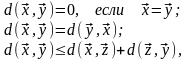
где х, у, z – элементы пространства, называется метрическим.
Совокупность п линейно независимых векторов образует n-мерное евклидово пространство Rn. Любой вектор , относящийся к Rn, определяется совокупностью его координат: = (x0, x1, …, xn-1). Пространство Rn можно определить как множество точек, представленных концами векторов, норма которых равна:
||
||
=
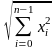 .
.
Расстояние между двумя векторами и определяется как норма разности векторов:
d(
,
)
= ||
-
||
=
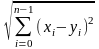 .
.
В Rn существует понятие скалярного произведения двух векторов и :
(
,
)
=
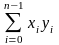 =
||
||∙||
||cosφ
, (2.1.8)
=
||
||∙||
||cosφ
, (2.1.8)
где φ – угол между двумя векторами.
Координаты вектора представляют собой проекции вектора на координатные оси. Из последнего соотношения (2.1.8) вытекает очевидное неравенство:
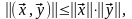 (2.1.9)
(2.1.9)
известное как
неравенство Буняковского-Шварца. Знак
равенства имеет место только при
коллинеарности (совпадении по форме)
векторов
и
,
т. е.
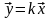 (k – скаляр).
(k – скаляр).
При п
→ ∞ пространство Rn
переходит в бесконечномерное
пространство Гильберта L2.
Гильбертовым пространством является,
в частности, пространство всех
непрерывных комплексных функций
аргумента t, заданных
на интервале
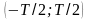 ,
в котором скалярное произведение и
квадрат нормы определены соотношениями:
,
в котором скалярное произведение и
квадрат нормы определены соотношениями:
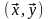 =
=
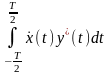 ,
(2.1.10)
,
(2.1.10)
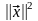 =
=
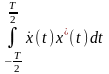 =
=
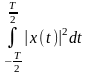 .
(2.1.11)
.
(2.1.11)
Элементы в L2 характеризуются интегрируемым квадратом: если элементы этого пространства – вещественные сигналы s(t), определенные на интервале , то выполняется условие:
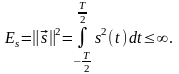 (2.1.12)
(2.1.12)
Гильбертово пространство обозначается при этом L2(T). При Т → ∞ получаем пространство L2(∞). Для некоторых сигналов пространства L2(∞) условие (2.1.12) при Т → ∞ может не выполняться, но выполняется условие:
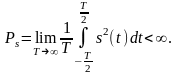 (2.1.13)
(2.1.13)
В этом случае можно вместо (2.1.10) ввести скалярное произведение с размерностью мощности (для токов и напряжений на единичном сопротивлении):
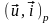 =
=
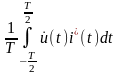 . (2.1.14)
. (2.1.14)
Квадрат нормы вектора в этом случае равен:
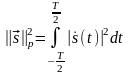 = P.
(2.1.15)
= P.
(2.1.15)
Квадрат расстояния между двумя векторами в вещественном пространстве L2(T) определяется соотношениями:
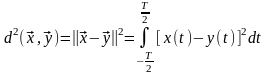 . (2.1.16)
. (2.1.16)
Пространство L2 представляет собой естественное обобщение пространства Rn, получаемое путём перехода от дискретизированной функции к функции непрерывного аргумента.
Пространство L2 имеет особое значение, т. к. оно позволяет применить общие геометрические представления к сообщениям, сигналам и помехам, определённым как функции непрерывного аргумента. Устремляя в (2.1.5) п → ∞, получаем представление непрерывной функции x(t) в пространстве Гильберта:
x(t)
=
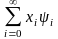 .
(2.1.17)
.
(2.1.17)
Функция x(t),
принимающая на каждом интервале i∆t
одно из т возможных значений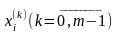 ,
на отрезке длительностью Т полностью
определена
,
на отрезке длительностью Т полностью
определена
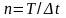 значениями
значениями
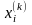 или, совокупностью коэффициентов
или, совокупностью коэффициентов
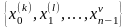
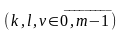 ,
называемой n-набором.
При m = 2 коэффициент
принимает значение 0 или 1, n-набор
представляет собой просто кодовую
комбинацию n - значного
двоичного (т = 2) кода, отображающую
символ (букву, цифру) передаваемого
сообщения. Двоичные п-наборы
отображаются векторами (точками) в
пространстве Хэмминга 2n.
Скалярное произведение в этом
пространстве задаётся функцией:
,
называемой n-набором.
При m = 2 коэффициент
принимает значение 0 или 1, n-набор
представляет собой просто кодовую
комбинацию n - значного
двоичного (т = 2) кода, отображающую
символ (букву, цифру) передаваемого
сообщения. Двоичные п-наборы
отображаются векторами (точками) в
пространстве Хэмминга 2n.
Скалярное произведение в этом
пространстве задаётся функцией:
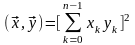 ,
,
где Σ – сумма в обычном смысле. Отсюда норма двоичного вектора:
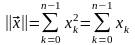
определяется количеством содержащихся в нём единиц. Эту норму называют также весом вектора (кодовой комбинации) и обозначают w. Расстояние в пространстве Хэмминга:
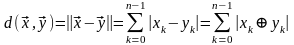 ,
,
где знак
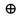 означает операцию суммирования по
модулю 2 (mod 2). В пространстве
Хэмминга расстояние между двоичными
векторами определяется по числу позиций
в кодовой комбинации, в которых
векторы
и
имеют различающиеся символы.
означает операцию суммирования по
модулю 2 (mod 2). В пространстве
Хэмминга расстояние между двоичными
векторами определяется по числу позиций
в кодовой комбинации, в которых
векторы
и
имеют различающиеся символы.
2.1.4 Операторы и функционалы
Эти два понятия расширяют понятие функции как математической модели сигнала.
Величина у = f(x) называется функцией независимой переменной х, если каждому значению х (из множества его возможных значений) соответствует определённое значение у.
Функционал устанавливает соответствие между множеством чисел, с одной стороны, и некоторым множеством функций – с другой. Функционал Ф устанавливает зависимость числа от функции: у = Ф[f(х)]. Примером функционала является определённый интеграл, величина которого (при неизменных пределах) зависит от вида подынтегральной функции.
Функциональный оператор устанавливает соответствие между двумя множествами функций, т.е. с помощью оператора L устанавливается зависимость функции от функции: y(f) = L[x(t)]. Так как функции могут быть представлены векторами и множество функций определяется как векторное пространство, то действие оператора может быть описано в геометрических терминах как преобразование пространства X векторов в пространство Y векторов . Обратное преобразование Y в X обозначают L-1. В задачах преобразования сообщений и сигналов используются наряду с линейными операторами также нелинейные и параметрические операторы.
Лекция 2.2 Разложение функций в ортогональные ряды по базисным функциям
2.2.1 Ортогональные системы функций и обобщенный ряд Фурье
Произвольную кусочно-непрерывную функцию f(х), для которой выполняется условие:
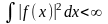 ,
(2.2.1)
,
(2.2.1)
можно представить в виде суммы ряда:
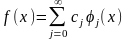 ,
(2.2.2)
,
(2.2.2)
где
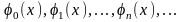 – бесконечная система действительных
функций, попарно ортогональных на
отрезке [а, b]:
– бесконечная система действительных
функций, попарно ортогональных на
отрезке [а, b]:
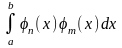 = 0 при n
≠ m;
= 0 при n
≠ m;
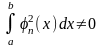 .
(2.2.3)
.
(2.2.3)
Интеграл в выражении (2.2.1) вычисляется по области определения f(х).
Функция
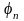 (х),
для которой выполняется условие:
(х),
для которой выполняется условие:
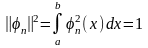 ,
(2.2.4)
,
(2.2.4)
называется
нормированной функцией, а система
нормированных функций
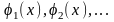 ,
в которой каждые две различные функции
взаимно ортогональны, называется
ортонормированной системой.
,
в которой каждые две различные функции
взаимно ортогональны, называется
ортонормированной системой.
Умножив обе части уравнения (2.2.2) на φn(х) и проинтегрировав в пределах а, b, получим:
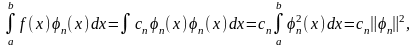
откуда следует важное соотношение:
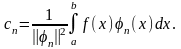 (2.2.5)
(2.2.5)
Ряд (2.2.2), в котором коэффициенты сп определены по формуле (2.2.5), называется обобщенным рядом Фурье по данной системе ортогональных функций φn(х).
Обобщенный ряд
Фурье при заданной системе функций
φn(х) и
при фиксированном числе слагаемых
ряда (2.2.2) обеспечивает наилучшую
аппроксимацию (в смысле минимума СКО)
данной функции f(х),
т.е. СКО
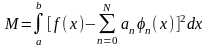 достигает минимума, когда коэффициенты
ряда ап = сп.
достигает минимума, когда коэффициенты
ряда ап = сп.
Ортогональная
система называется полной, если
среднеквадратическую ошибку М можно
сделать сколь угодно малой при увеличении
числа членов в ряде, т.е.
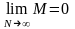 .
Условием полноты является соотношение
.
Условием полноты является соотношение
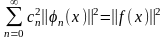 ,
которое применительно к сигналам s(t)
имеет энергетический смысл:
,
которое применительно к сигналам s(t)
имеет энергетический смысл:
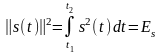 ,
(2.2.8)
,
(2.2.8)
где Es – энергия сигнала в промежутке t2 – t1, выделяемая на резисторе с сопротивлением 1 Ом.
В соответствии с этой формулой энергия сигнала:
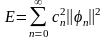 ,
(2.2.9)
,
(2.2.9)
а при использовании ортонормированной системы функций φn(t):

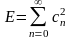 .
(2.2.10)
.
(2.2.10)
Промежуток времени t2 – t1 , в котором определяется E, является интервалом ортогональности для системы функций φn(t).
Средняя за время t2 – t1 мощность сигнала равна:
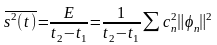 .
(2.2.11)
.
(2.2.11)
Выбор наиболее рациональной ортогональной системы функций зависит от цели, преследуемой при разложении сложной функции в ряд. Среди разнообразных задач, требующих разложения сложного сигнала, наиболее важными являются:
- точное разложение на простейшие ортогональные функции;
- аппроксимация сигналов, процессов или характеристик, когда требуется свести к минимуму число членов ряда (при заданной допустимой погрешности).
При решении первой задачи наибольшее распространение получила ортогональная система основных тригонометрических функций – синусов и косинусов. При решении второй задачи – приближенном разложении функций – применяются разнообразные ортогональные системы функций: полиномы Чебышева, Эрмита, Лагерра, Лежандра и многие другие.
2.2.2 Спектральное представление периодических функций
Периодическую функцию x(t) = x(t - пТ) (T – период повторения) можно представить в виде обобщённого ряда Фурье по базисным функциям основной тригонометрической системы, попарно ортогональным на интервале (-T/2; Т/2):
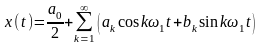 ;
;
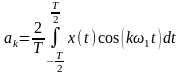 ,
,
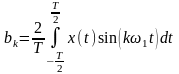 .
(2.2.12)
.
(2.2.12)
Этот ряд можно записать в виде:
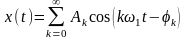 ;
;
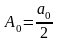 ,
,
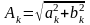 ,
,
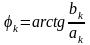 ,
(2.2.13)
,
(2.2.13)
т.е. периодическую
функцию x(t)
можно представить суммой гармонических
колебаний с частотами, кратными
основной частоте f1
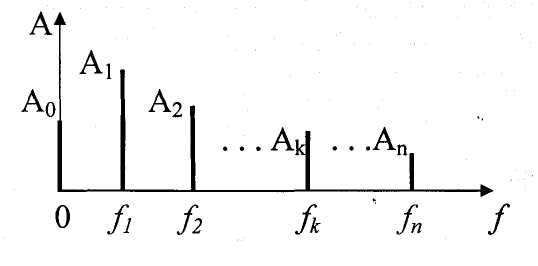
= 1/T (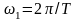 )
с амплитудами Аk
и начальными фазами φk.
Совокупность амплитуд Аk
(k = 0, 1, 2, ...)
образует амплитудный спектр, а
совокупность фаз φk
(k = 0, 1,
2, ...) – фазовый спектр функции.
Линейчатый амплитудный спектр
периодической функции х(t)
изображён на рисунке 2.2.1.
)
с амплитудами Аk
и начальными фазами φk.
Совокупность амплитуд Аk
(k = 0, 1, 2, ...)
образует амплитудный спектр, а
совокупность фаз φk
(k = 0, 1,
2, ...) – фазовый спектр функции.
Линейчатый амплитудный спектр
периодической функции х(t)
изображён на рисунке 2.2.1.
Воспользовавшись формулой Эйлера:
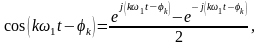
ряд Фурье (2.2.13) можно представить в комплексной форме:
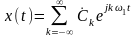 ,
(2.2.14)
,
(2.2.14)
где
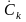 – комплексная амплитуда, определяемая
по формуле:
– комплексная амплитуда, определяемая
по формуле:
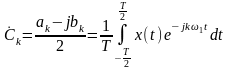 .
(2.2.15)
.
(2.2.15)
Сумма в (2.2.14)
охватывает как положительные, так и
отрицательные значения k
(появляются «отрицательные частоты»).
Это выражение можно интерпретировать
как представление гармонического
сигнала единичной амплитуды с положительной
частотой
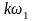 в виде суммы двух гармонических
колебаний (половинной амплитуды) на
положительной
и отрицательной частоте -
(рис. 2.2.2).
в виде суммы двух гармонических
колебаний (половинной амплитуды) на
положительной
и отрицательной частоте -
(рис. 2.2.2).
Для вещественных функций x(t) амплитудный спектр – чётная функция частоты аk = а-k, bk = -b-k, Ak = А-k, фазовый – нечётная функция частоты φk = -φ-k(,). Как следствие:
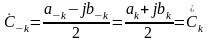 ,
,
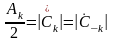 ,
,
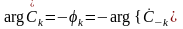 .
.
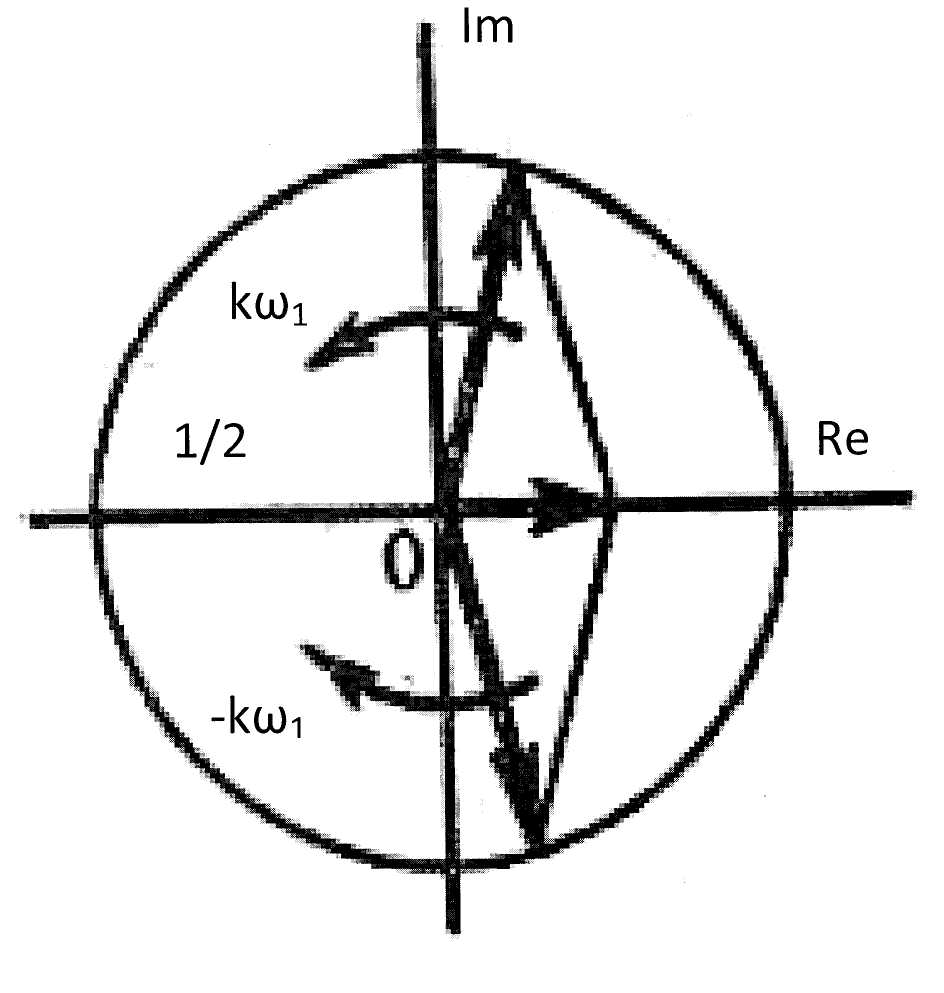 Рисунок
2.2.2 – Представление гармонического
колебания в виде двух комплексных
составляющих с положительной и
Рисунок
2.2.2 – Представление гармонического
колебания в виде двух комплексных
составляющих с положительной и
отрицательной частотами
2.2.3 Спектральное представление непериодических функций
Разложение в тригонометрический ряд Фурье (2.2.14) может быть обобщено на случай непериодических функций х(t) путём устремления Т → ∞ или f1 = 1/Т → 0:
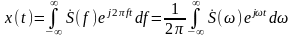 ,
(2.2.16)
,
(2.2.16)
где
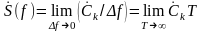 – спектральная
плотность
(СП) непериодического сигнала,
– спектральная
плотность
(СП) непериодического сигнала,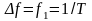 – частотный разнос между линиями
спектра периодического сигнала, т.е.
непериодическая функция x(t)
представляется
суммой гармонических компонент
– частотный разнос между линиями
спектра периодического сигнала, т.е.
непериодическая функция x(t)
представляется
суммой гармонических компонент
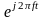 (на
положительных и отрицательных частотах)
с бесконечно малыми амплитудами
(на
положительных и отрицательных частотах)
с бесконечно малыми амплитудами
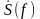 df.
Модуль
df.
Модуль
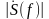 определяет
сплошной (непрерывный) спектр
непериодического сигнала, a
arg
=
определяет
сплошной (непрерывный) спектр
непериодического сигнала, a
arg
=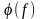 – сплошной
(непрерывный) фазовый спектр непериодического
сигнала.
– сплошной
(непрерывный) фазовый спектр непериодического
сигнала.
Исходя из определения с учётом (2.2.15) следует формула для определения СП:
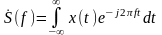 .
(2.2.17)
.
(2.2.17)
Спектр по Фурье можно записать в виде:
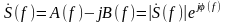 ,
(2.2.18)
,
(2.2.18)
где
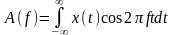 – чётная,
– чётная,
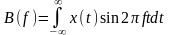 – нечётная функция частоты.
– нечётная функция частоты.
Из последних
выражений видно, что для вещественных
функций х(t)
амплитудный спектр
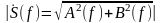 является чётной функцией частоты,
фазовый спектр
является чётной функцией частоты,
фазовый спектр
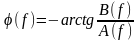 – нечётная функция частоты. Дискретный
(линейчатый) спектр амплитуд
– нечётная функция частоты. Дискретный
(линейчатый) спектр амплитуд
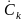 периодической функции х(t)
= x(t
+ nT) можно найти
по формуле:
периодической функции х(t)
= x(t
+ nT) можно найти
по формуле:
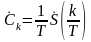 .
(2.2.19)
.
(2.2.19)
Пара преобразований
Фурье x(t)
→
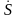 (f)
(прямое) и
(f)
→ х(t) (обратное)
описывается линейным оператором. Поэтому
для этих преобразований справедлив
принцип суперпозиции (наложения): СП
сигнала
(f)
(прямое) и
(f)
→ х(t) (обратное)
описывается линейным оператором. Поэтому
для этих преобразований справедлив
принцип суперпозиции (наложения): СП
сигнала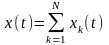 определяется
суммой СП слагаемых хk(t).
определяется
суммой СП слагаемых хk(t).
Скалярное произведение функций x(t) и y(t) (в общем случае комплексных) в пространстве Гильберта L2(T) можно выразить и через их СП по Фурье:
(x,y)
=
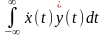 =
=
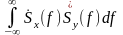 .
(2.2.20)
.
(2.2.20)
Это соотношение называют обобщённой формулой Рэлея (или соотношением Парсеваля).
В ТЭС важную роль
играют характеристики
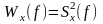 и
и
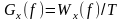 =
=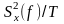 ,
имеющих смысл соответственно спектральной
плотности энергии (СПЭ):
,
имеющих смысл соответственно спектральной
плотности энергии (СПЭ):
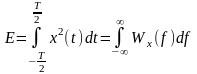 (2.2.21)
(2.2.21)
и мощности (СПМ) сигнала длительностью T:
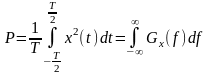 .
(2.2.22)
.
(2.2.22)
По определению эти характеристики являются чётными функциями частоты, следовательно, можно записать:
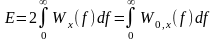 ,
,
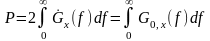 ,
(2.2.23)
,
(2.2.23)
где
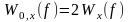 и
и
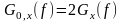 – СПЭ и СПМ, определённые на
положительных частотах.
– СПЭ и СПМ, определённые на
положительных частотах.
2.2.4 Представление функций полиномами Лежандра, Чебышева, Лагерра, Эрмита, функциями Хаара, Радемахера и Уолша
В тех случаях, когда требуется аппроксимировать заданную функцию f(x) с помощью ограниченного числа членов ряда, применяют различные ортогональные системы специальных не гармонических функций. Условия ортонормированности этих функций на заданном интервале (a, b) записываются в форме:
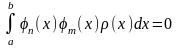 при n
≠ m.
при n
≠ m.
Множитель
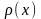 под знаком интеграла называется
весовой функцией (функцией веса).
Говорят, что функции
под знаком интеграла называется
весовой функцией (функцией веса).
Говорят, что функции
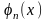 и
и
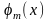 ортогональны
с весом
,
т.е. ортогональны функции
ортогональны
с весом
,
т.е. ортогональны функции
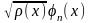 .
.
Для представления непрерывных сигналов наиболее употребительны ортогональные полиномы и функции:
- Лежандра [ = 1, а = - 1, b = 1];
- Чебышева [ = (1 – t2)-1/2, а = - 1, b = 1];
- Лагерра [ = tαe-t, а = 0, b = ∞];
- Эрмита [
=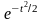 ,
а = - ∞, b = ∞];
,
а = - ∞, b = ∞];
- Якоби [ = (1 –t)λ(1 + t)μ, а = - 1, b = 1] и т.д.
Для представления дискретных сигналов широкое распространение получили кусочно-постоянные функции Хаара, Радемахера и Уолша.
Тип разложения выбирают из соображения удобства.
2.2.5 Теорема Котельникова
В настоящее время широкое распространение получили цифровые системы связи. По каналам таких систем все виды сообщений, в том числе и аналоговые, передаются в цифровой форме. Это обусловлено, прежде всего, следующими достоинствами цифровых сигналов:
- их большей устойчивостью к возможным искажениям в канале;
- возможностью непосредственного ввода информации для последующей обработки в цифровых ЭВМ;
- возможностью преобразований непрерывного сигнала в цифровой и обратно практически с любой заданной точностью.
Первой операцией, выполняемой при преобразовании аналогового (непрерывного) сигнала в дискретный (цифровой) является его дискретизация.
Теорема Котельникова (отсчетов, Найквиста), лежащая в основе дискретизации, формулируется следующим образом: непрерывный сигнал s(t), спектр которого ограничен сверху частотой FB, полностью определяется отсчетами мгновенных значений s(k∆t) в точках, отстоящих друг от друга на интервалы ∆t ≤ l/2FВ. Интервал ∆t называется интервалом Котельникова (Найквиста), а fд = 1/∆t – частотой дискретизации. Эта теорема позволяет представить непрерывную функцию s(t) в виде ряда Котельникова:
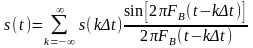 .
(2.2.24)
.
(2.2.24)
Базисными в разложении Котельникова являются так называемые функции отсчёта вида:
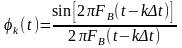 ,
(2.2.25)
,
(2.2.25)
обладающие следующими свойствами:
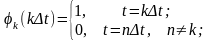
- спектральная
плотность функции
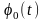 равномерна
в полосе частот |f|
< FB
и равна
равномерна
в полосе частот |f|
< FB
и равна
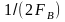 ;
;
- функции отсчетов ортогональны с весом единица на бесконечном интервале времени.
Ряд Котельникова точно определяет функцию s(t) в точках отсчета (коэффициентами ряда являются сами выборки из функции s(k∆t)) и определяет функцию s(t) в любой момент t (рис. 2.2.3).
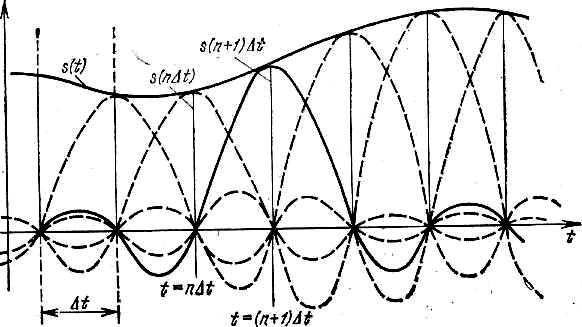
Рисунок 2.2.3 – Представление сигнала рядом Котельникова
Теоретически дискретизация осуществляется с помощью -импульсов:
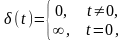
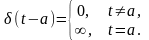
Отсчёты функции
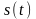 получаются
в результате её перемножения на
периодическую последовательность
-
импульсов
получаются
в результате её перемножения на
периодическую последовательность
-
импульсов
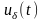 с
периодом Т = t,
спектр которой является дискретным
(рис. 2.2.4):
с
периодом Т = t,
спектр которой является дискретным
(рис. 2.2.4):
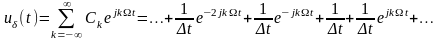 ,
,
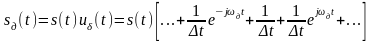 –
дискретизированный
сигнал,
–
дискретизированный
сигнал,
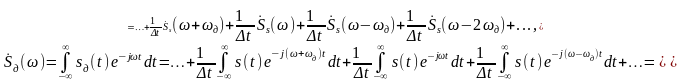 где
где
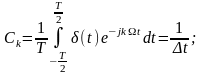
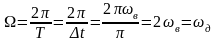 – частота дискретизации, s(t)
– исходный сигнал, uδ(t)
– последовательность
-
импульсов,
– частота дискретизации, s(t)
– исходный сигнал, uδ(t)
– последовательность
-
импульсов,
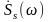 –
спектр исходного сигнала
.
–
спектр исходного сигнала
.
- импульсов
Спектр дискретизированного сигнала (рис. 2.2.5, б) содержит спектры исходного сигнала Ss() (рис. 2.2.5, а), тот же спектр, смещённый на величину, кратную частоте дискретизации вправо Ss( - nд), и влево Ss( + nд), n = 1, 2, 3, ….
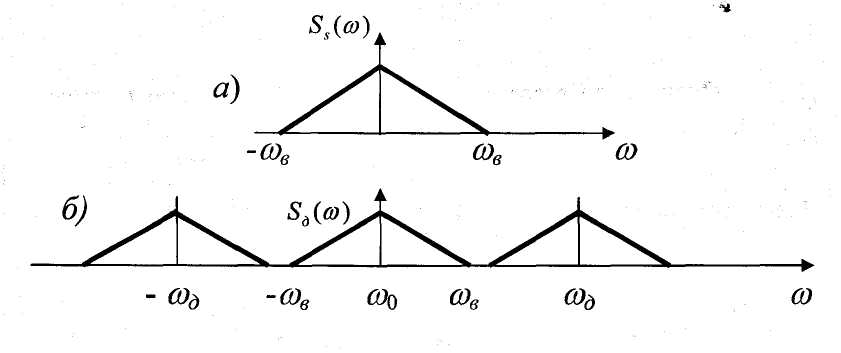
Рисунок 2.2.5 – Спектр исходного (а) и дискретизированного
(б) сигналов
В реальных системах связи дискретизация осуществляется последовательностью импульсов, имеющих, в отличие от - импульсов, конечную длительность. В результате процесса дискретизации получается последовательность реальных, например, прямоугольных импульсов, амплитуда которых соответствует значениям непрерывного сигнала в тактовые моменты времени (амплитудно-импульсная модуляция АИМ):
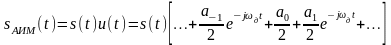 ,
,
где – периодическая последовательность импульсов.
В квадратных скобках – ряд Фурье для последовательности импульсов конечной длительности. Спектр АИМ сигнала аналогичен спектру дискретизированного сигнала при дискретизации -импульсами, но амплитуда составляющих спектра убывает с ростом номера гармоники (рис. 2.2.6) :
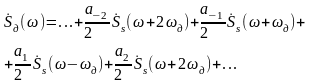
Восстановление
исходного сигнала по последовательности
отсчетов осуществляется путем формирования
для каждого отсчета s(k∆t)
функции
 с соответствующей амплитудой и последующим
суммированием всех функций (рис 2.2.7)
с соответствующей амплитудой и последующим
суммированием всех функций (рис 2.2.7)
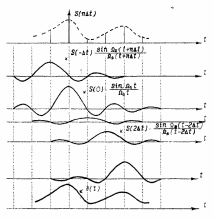
Рисунок 2.2.7 – Восстановления исходной функции по
последовательности отсчетов
Устройством, формирующим отклик вида (six)/x при воздействии δ – импульса, является идеальный фильтр нижних частот (ИФНЧ) с АЧХ и ИХ характеристиками, представленными на рис. 2.2.8.
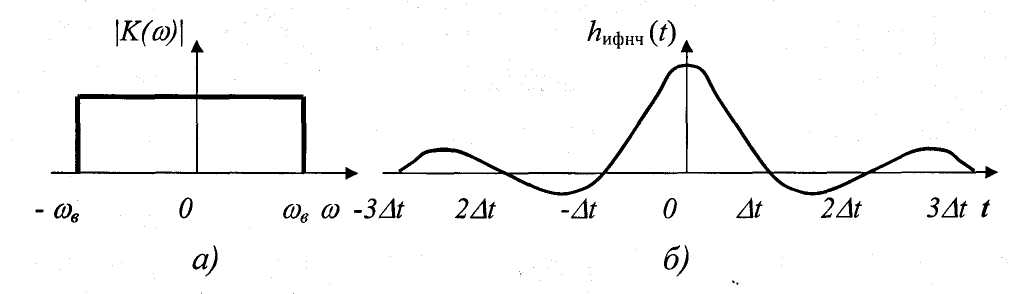
Рисунок 2.2.8 – АЧХ (а) и ИХ (б) ИФНЧ
Реальные сигналы,
имеющие конечную длительность и
неограниченный спектр, не соответствуют
в точности модели сигнала с ограниченным
спектром, и применение к ним теоремы
Котельникова связано с погрешностями
при восстановлении сигналов по ряду
Котельникова и неопределенностью
выбора шага дискретизации
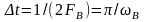 или частоты дискретизации fд.
Для практических условий достаточно
восстановление функций с заданной
точностью. Поэтому теорема Котельникова
является приближенной для функций с
неограниченным спектром. Погрешность
дискретизации определяется энергией
спектральных составляющих сигнала,
лежащих за пределами частоты в
=2πFв:
или частоты дискретизации fд.
Для практических условий достаточно
восстановление функций с заданной
точностью. Поэтому теорема Котельникова
является приближенной для функций с
неограниченным спектром. Погрешность
дискретизации определяется энергией
спектральных составляющих сигнала,
лежащих за пределами частоты в
=2πFв:
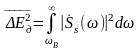 .
(2.2.26)
.
(2.2.26)
На практике частоту отсчетов часто определяют по формуле:
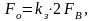 (2.2.27)
(2.2.27)
где kз
– коэффициент запаса, обычно 1,5 ≤ kз
≤ 6;
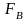 – принятая из некоторых соображений
верхняя частота в спектре сигнала
s(t),например,
с учетом доли полной энергии, сосредоточенной
в ограниченном частотой
спектре сигнала.
– принятая из некоторых соображений
верхняя частота в спектре сигнала
s(t),например,
с учетом доли полной энергии, сосредоточенной
в ограниченном частотой
спектре сигнала.
Лекция 2.3 Случайные процессы и их основные характеристики
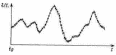
Случайными называются процессы X(t), реализации которых в каждом опыте точно предсказать невозможно. В отличие от детерминированных для них нельзя заранее утверждать, что X(t) в некоторый момент t будет иметь определённое значение. Например, для непрерывного случайного процесса (СП) можно лишь говорить о некоторой вероятности того, что в этот момент значение X(t) окажется в интервале между значениями х и х + ∆х, т.е. её значения при фиксированном значении аргумента представляют собой случайные величины Х(ti) = Xi.
Случайность процесса X(t) проявляется в том, что вид наблюдаемой функции случайным образом меняется от одного наблюдения к другому. Получаемая в результате каждого отдельного опыта функция х(t) не случайна. Её называют реализацией случайной функции. Совокупность всех возможных реализаций {x(r)(t)} образует СП (или случайную функцию) X(t) = {x(r)(t)}. Для непрерывного СП число реализаций образует несчётное множество.
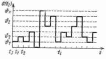
На рис. 2.3.1 показаны четыре реализации СП. Наличие случайности результатов многократных наблюдений одного и того же процесса не означает отсутствие в этом процессе никаких закономерностей: средние результаты, найденные по большому числу наблюдений, устойчивы, т.е. случайные явления и процессы подчиняются определённым статистическим закономерностям.
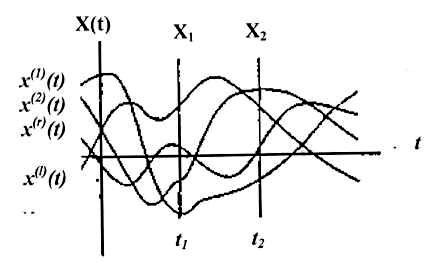
Рисунок 2.3.1 – Задание СП через совокупность его реализаций
Если на графике множества реализаций СП X(t) выбрать сечение t1, то множество {x(r)(t1)} значений реализаций в этот момент образует случайную величину (СВ) X. Значения этой СВ заранее неизвестны. Но можно установить некоторые закономерности, по которым можно судить о том, что в данном сечении СВ с вероятностью р будет принимать значение в определённых пределах [х, х + ∆х].
2.3.1 Плотность вероятности и интегральная функция распределения
Для непрерывных СП X(t) распределение вероятностей в заданном сечении t1 характеризуется одномерной плотностью вероятностей (ПВ):
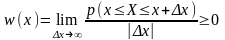 ,
,
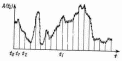
выражающей отношение вероятности того, что СВ X(t) примет значения в интервале x ≤ X ≤ х + ∆х, к величине интервала ∆х. На рис. 2.3.2, а изображён типовой график одномерной ПВ.
Вероятность того, что СВ X примет значение в интервале (х1; х2) определяется выражением:
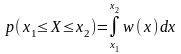 .
.
Интеграл в бесконечных пределах от функции w(x) равен единице 1 (условие нормировки для достоверного события):
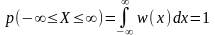 .
.
Другой важной характеристикой СВ X является интегральная функция распределения (ИФР) F(x), определяемая как вероятность того, что СВ X не превзойдёт некоторого значения х:
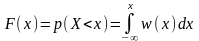 .
.
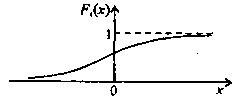
График ИФР F(x) приведён на рис. 2.3.2, б.

a) б)
Рисунок 2.3.2 – Типовой график одномерной ПВ (а) и одномерной ИФР (б)
В прикладных задачах часто предполагают, что ИФР являются дифференцируемыми функциями и определяют w(x) как производную от ИФР:
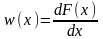 .
(2.3.1)
.
(2.3.1)
Основные сведения об этих законах и их свойствах приведены в таблице 2.3.1.
Таблица 2.3.1 – Основные свойства ИФР и ПВ случайной величины
Название и обозначение |
Функция распределения F(x) |
Плотность вероятности w(x) |
Определение |
|
|
Физическая размерность |
безразмерная |
размерность
|
Взаимосвязь |
|
|
Особенности функции |
F(x2)F(x1) при x2x1 (неубывающая) |
w(x)0 (неотрицательная) |
Расчет вероятности
|
|
|
Свойство нормировки |
|
|
Для более полного описания СП нужно располагать его n-мерной ПВ w(x1, х2, ..., хn; t1, t2, ..., tn) или n-мерной ИФР F(x1, x2, ..., хn; t1, t2, ..., tn), выражающих свойства СП в произвольных сечениях t1, t2, ..., tn. В общем случае n-мерная ПВ определяется аналогично (2.3.1) как:
 .
.
2.3.2 Числовые характеристики
На практике часто ограничиваются рассмотрением менее полных, но более простых характеристик СП, называемых числовыми характеристиками или моментами. Числовыми характеристиками СП могут служить начальный и центральный момент k-го порядка, определяемые соответственно как:
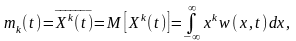
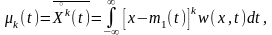
где
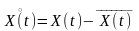 – разность между СВ Х
и её
математическим ожиданием,
представляющая
собой отклонение СВ от среднего значения,
называется центрированным
значением
СВ. Черта сверху означает усреднение
по множеству реализаций. Моменты
полностью определяются одномерным
распределением и в общем случае
произвольного СП являются детерминированными
функциями времени. В частности, начальный
момент первого порядка
– разность между СВ Х
и её
математическим ожиданием,
представляющая
собой отклонение СВ от среднего значения,
называется центрированным
значением
СВ. Черта сверху означает усреднение
по множеству реализаций. Моменты
полностью определяются одномерным
распределением и в общем случае
произвольного СП являются детерминированными
функциями времени. В частности, начальный
момент первого порядка
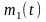 называется
начальный математическим
ожиданием СВ
(МО):
называется
начальный математическим
ожиданием СВ
(МО):
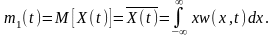 (2.3.2)
(2.3.2)
Центральный момент второго порядка называется дисперсией:
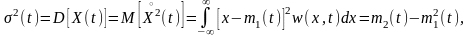 (2.3.3)
(2.3.3)
Величина
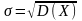 называется стандартным или
среднеквадратическим отклонением.
Дисперсия характеризует разброс СВ
относительно её среднего значения.
называется стандартным или
среднеквадратическим отклонением.
Дисперсия характеризует разброс СВ
относительно её среднего значения.
МО
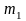 и дисперсия
и дисперсия
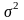 являются
важными характеристиками СВ, однако
они не дают достаточного представления
об изменчивости СП во времени. При
совместном исследовании СВ X(t1)
и X(t2)
сечений t1
и t2
вводится
понятие смешанного центрального момента
второго порядка, называемого функцией
корреляции
(ФК):
являются
важными характеристиками СВ, однако
они не дают достаточного представления
об изменчивости СП во времени. При
совместном исследовании СВ X(t1)
и X(t2)
сечений t1
и t2
вводится
понятие смешанного центрального момента
второго порядка, называемого функцией
корреляции
(ФК):
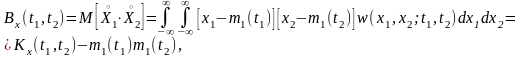 где
где
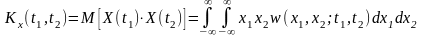 –
ковариационная
функция;
w(x1,
x2;
t1,
t2)
– двумерная
плотность вероятности.
–
ковариационная
функция;
w(x1,
x2;
t1,
t2)
– двумерная
плотность вероятности.
ФК характеризует степень статистической взаимосвязи значений Х1 и Х2 СП Х(t) в моменты t1 и t2, разделённые интервалом τ = t2 – t1. Убывание ФК с увеличением τ свидетельствует об ослаблении связи между мгновенными значениями процесса. Отрицательное значение ФК при каких-либо значениях τ свидетельствует о том, что положительным отклонениям процесса в одном сечении соответствуют преимущественно отрицательные отклонения в другом сечении и наоборот. Если СВ Х1 и Х2 статистически независимы, то их двумерная ПВ определяется произведением одномерных ПВ: w(x1, х2; t1, t2) = w(x1; t1)w(х2; t2); ФК между двумя такими сечениями равна нулю.
2.3.3 Стационарные случайные процессы
СП можно разделить на стационарные и нестационарные. Стационарным СП в строгом смысле называется такой СП, для которого ПВ (или ИФР) любого порядка не зависит от сдвига процесса во времени на произвольную величину τ. Это означает, что для любых n и τ справедливо равенство:
w(x1, х2, ..., хn; t1, t2, ..., tn) = w(x1, х2, ..., хn; t1 - τ , t2 - τ, ..., tn- τ).
Отсюда следует, что все одномерные ПВ должны быть идентичными, т.е. не должны зависеть от времени:
w(x, t)= w(x, t – τ) = w(x). (2.3.4)
Все двумерные ПВ могут зависеть только от интервала τ = t2 – t1:
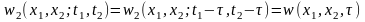 (2.3.5)
(2.3.5)
и не зависят от положения этого интервала во времени.
Стационарным СП в широком смысле называется такой СП, свойства которого описываются только одномерной ПВ, удовлетворяющей условию (2.3.4) и двумерной ПВ, удовлетворяющей условию (2.3.5). Соответственно для СП, стационарного в широком смысле, параметры т1 и σ2 не зависят от времени, а ФК зависит только от τ. Из определения стационарности в широком смысле, СП следует, что его ФК – чётная функция от τ: В(τ) = В(-τ).
2.3.4 Эргодические процессы
Дальнейшее упрощение анализа СП достигается при использовании условия эргодичности процесса. Стационарный СП называется эргодическим, если усреднение любой его вероятностной характеристики по множеству реализаций эквивалентно усреднению по времени одной теоретически бесконечно длинной реализации. Условие эргодичности СП включает в себя и условие его стационарности.
Достаточное условие (условие Слуцкого) эргодичности стационарного (в широком смысле) СП можно записать в виде:
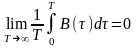 .
.
В соответствии с определением эргодического процесса выражения для его основных параметров выглядят следующим образом (волнистой чертой обозначена операция усреднения по времени):
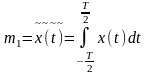 ,
,
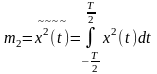 ,
,
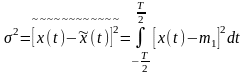 ,
,
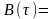
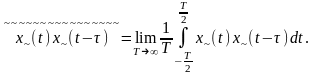
ФК эргодического СП также можно получить усреднением во времени:
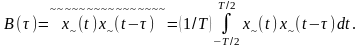
Если x(t)
представляет собой электрический
сигнал, то
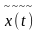 –
постоянная составляющая СП,
–
постоянная составляющая СП,
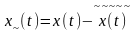 – переменная составляющая СП,
– переменная составляющая СП,
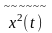 – средняя мощность СП, σ2
– средняя мощность переменной составляющей
СП.
– средняя мощность СП, σ2
– средняя мощность переменной составляющей
СП.
Графики типовых ФК приведены на рис. 2.3.3.
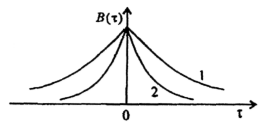
Рисунок 2.3.3 – Функция корреляции СП с медленно (1) и
быстро (2) убывающими связями
Основные свойства ФК стационарного эргодического СП:
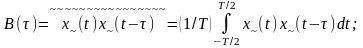
ФК чётная
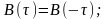
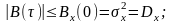
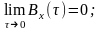
КФ характеризует статистическую связь сечений внутри СП. Если связь между сечениями X(t1) и X(t2) отсутствует, то
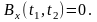 Отсутствие связи влечёт отсутствие
корреляции, но не наоборот. Только для
нормального СП отсутствие корреляции
влечёт отсутствие связи;
Отсутствие связи влечёт отсутствие
корреляции, но не наоборот. Только для
нормального СП отсутствие корреляции
влечёт отсутствие связи;для абстрагирования от дисперсии (учитываются только связи внутри СП) используют нормированную ФК (коэффициент корреляции):
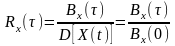 ;
;
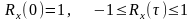 ;
;
интервал корреляции равен основанию прямоугольника с высотой, равной единице, площадь которого равна площади под кривой
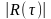 при
при
 (рис. 2.3.4) и определяют методом равновеликого
прямоугольника:
(рис. 2.3.4) и определяют методом равновеликого
прямоугольника:
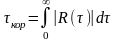 ;
;
8) взаимная ФК двух процессов X(t) и Y(t) равна:
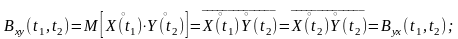
ФК суммы независимых СП Z(t) = X(t) + Y(t) равна:
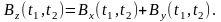
2.3.5 Нормальное (гауссовское) распределение
Нормальный
(гауссов) закон распределения СВ чаще
других встречается в природе. Нормальный
процесс особенно характерен для помех
канала связи. Он особенно удобен для
анализа. Поэтому СП, распределение
которых не слишком сильно отличается
от нормального, часто заменяют нормальным
процессом. Кроме того, в соответствии
с центральной предельной теоремой
теории вероятности сумма независимых
СВ х1, х2, …,
хn, имеющих
одинаковое распределение с конечной,
отличной от нуля дисперсией
,
при n → ∞ стремится
к нормальному распределению со средним
значением
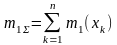 и дисперсией
и дисперсией
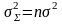 .
Одномерная ПВ нормального процесса
определяется выражением:
.
Одномерная ПВ нормального процесса
определяется выражением:
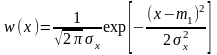 .
(2.3.6)
.
(2.3.6)
Это распределение
полностью определяется двумя параметрами:
МО т1 и дисперсией
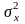 .
.
Свойства нормального СП:
ПВ положительная
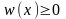 ;
;ПВ симметрична относительно x = m1;
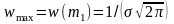 ;
;;
при изменении m1 кривая без изменения формы смещается вдоль оси х;
чем больше дисперсия , тем меньше величина максимума ПВ и тем она шире;
с вероятностью
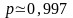 мгновенные
значения нормального СП находятся в
пределах
мгновенные
значения нормального СП находятся в
пределах
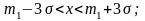
ИФР, соответствующая нормальному закону, имеет вид:
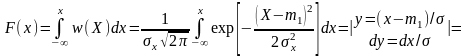
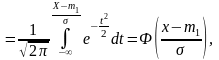
где
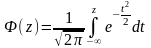 – неэлементарная табулированная
функция, называемая интегралом
вероятности, представляет собой
вероятность того, что нормированное
случайное отклонение не превзойдет
величину z.
– неэлементарная табулированная
функция, называемая интегралом
вероятности, представляет собой
вероятность того, что нормированное
случайное отклонение не превзойдет
величину z.
Вероятность того, что нормальная СВ X не выйдет за пределы интервала [x1, x2] равна:
р(x1
≤ X ≤ x2)
=
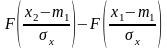 .
.
На рисунке 2.3.5 приведен вид нормального закона для различных значений при m1 = 0.
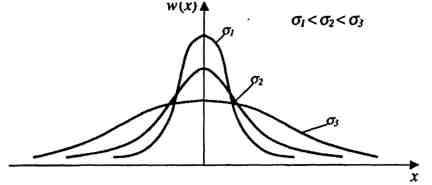
Рисунок 2.3.5 – Нормальный закон распределения
Лекция 2.4 Спектральный анализ случайных процессов. Ортогональные разложения случайных функций
2.4.1 Спектральный анализ случайных процессов
Для
описания СП наряду с ФК
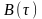 широко
используются спектральные
характеристики, в частности спектральная
плотность мощности (СПМ)
широко
используются спектральные
характеристики, в частности спектральная
плотность мощности (СПМ)
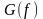 ,
называемая также энергетическим
спектром (ЭС) СП.
,
называемая также энергетическим
спектром (ЭС) СП.
ЭС стационарного СП и его ФК связаны между собой парой интегральных преобразований Фурье, что было строго доказано Н. Винером и А.Я. Хинчиным (теорема Винера-Хинчина):
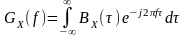 ,
, 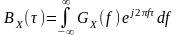 . (2.4.1)
. (2.4.1)
Средняя
мощность функции
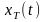 ,
совпадающей с реализацией СП
на интервале
,
совпадающей с реализацией СП
на интервале
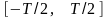 ,
при
,
при
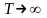 равна:
равна:
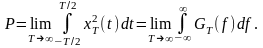
Предел
функции под интегралом в этом выражении
определяет СПМ, т.е.
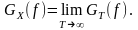 Строго говоря, это определение справедливо
только для эргодических СП, т.к. оно
характеризует распределение мощности
по частоте единственной реализации
Строго говоря, это определение справедливо
только для эргодических СП, т.к. оно
характеризует распределение мощности
по частоте единственной реализации
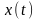 .
Для определения СПМ совокупности
реализаций
.
Для определения СПМ совокупности
реализаций
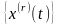 необходимо провести усреднение по
ансамблю возможных значений
необходимо провести усреднение по
ансамблю возможных значений
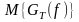 .
.
ЭС СП обладают следующими свойствами:
1)
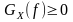 .
Из этого факта и теоремы Винера – Хинчина
вытекает важное следствие для
корреляционной функции
.
Из этого факта и теоремы Винера – Хинчина
вытекает важное следствие для
корреляционной функции
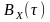 – она является положительно
определенной, т.е. имеет неотрицательное
преобразование Фурье.
– она является положительно
определенной, т.е. имеет неотрицательное
преобразование Фурье.
2)
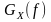 – четная функция:
– четная функция:
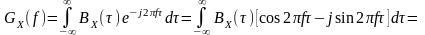
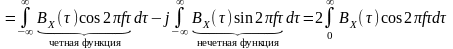 .
.
На этом свойстве основано понятие одностороннего ЭС, существующего только в области положительных частот
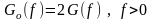 .
.
3)
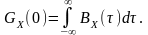
4)
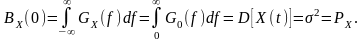
5) Нормированный энергетический спектр:
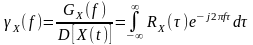 ,
,
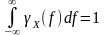 .
.
6) Эффективная ширина спектра – величина площади под кривой одностороннего энергетического спектра, отнесенная к спектральной плотности на некоторой характерной частоте f0 (обычно соответствующей максимуму спектральной плотности):
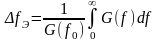 .
.
Произведение
эффективной ширины спектра
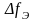 на интервал корреляции τкор величина
приближенно постоянная
τкор ≈ const.
на интервал корреляции τкор величина
приближенно постоянная
τкор ≈ const.
2.4.2 Примеры энергетических спектров некоторых стационарных СП
СП,
характеризуемый равномерной на всех
частотах СПМ
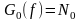 ,
называют «белым шумом» (рис. 2.4.1, а).
Если спектр
,
называют «белым шумом» (рис. 2.4.1, а).
Если спектр
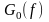 ограничен сверху частотой
ограничен сверху частотой
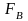 ,
то процесс называется «квазибелым
шумом» (рис. 2.4.1, б), его дисперсия
,
то процесс называется «квазибелым
шумом» (рис. 2.4.1, б), его дисперсия
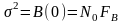 .
.
Корреляционная функция квазибелого шума имеет вид (рис. 2.4.2):

Рисунок 2.4.1 – СПМ белого (а) и квазибелого (б) шума
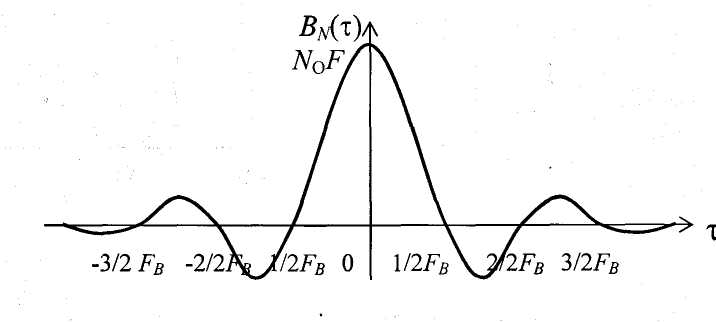
При
 ,
где k – целое число,
значения
проходят через нуль. Это означает, что
сечения процесса, разделённые интервалом
,
не коррелированны между собой. Устремив
,
где k – целое число,
значения
проходят через нуль. Это означает, что
сечения процесса, разделённые интервалом
,
не коррелированны между собой. Устремив ,
от квазибелого шума приходим к абсолютно
СП (белому шуму), у которого два
несовпадающих сечения не коррелированны:
ФК белого шума выражается
-
функцией:
,
от квазибелого шума приходим к абсолютно
СП (белому шуму), у которого два
несовпадающих сечения не коррелированны:
ФК белого шума выражается
-
функцией:
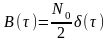 .
.
Белый
шум является математической идеализацией
реального процесса, т.к. средняя мощность
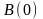 ,
необходимая для создания такого процесса,
оказывается бесконечно большой. Вместе
с тем, случаи, когда спектр реальной
помехи можно аппроксимировать белым
шумом, на практике встречаются достаточно
часто. Примером такой помехи является
тепловой шум (
,
необходимая для создания такого процесса,
оказывается бесконечно большой. Вместе
с тем, случаи, когда спектр реальной
помехи можно аппроксимировать белым
шумом, на практике встречаются достаточно
часто. Примером такой помехи является
тепловой шум (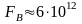 Гц).
Гц).
2.4.3 Ортогональные разложения случайных функций
Ортогональные
разложения детерминированных сигналов
можно использовать также для отдельных
реализаций СП. По отношению к СП в целом
коэффициенты такого разложения меняются
от реализации к реализации. Следовательно,
СП на интервале
 можно разложить в ряд по детерминированным
функциям
можно разложить в ряд по детерминированным
функциям
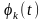 :
:
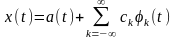 ,
(2.4.2)
,
(2.4.2)
где
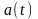 – среднее значение случайного процесса,
а
– среднее значение случайного процесса,
а
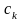 – коэффициенты разложения, являющиеся
случайными величинами. Для СП сходимость
этого ряда (2.4.2) необходимо понимать в
среднеквадратичном смысле:
– коэффициенты разложения, являющиеся
случайными величинами. Для СП сходимость
этого ряда (2.4.2) необходимо понимать в
среднеквадратичном смысле:
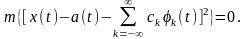 (2.4.3)
(2.4.3)
При выборе функций
разложения для СП необходимо учитывать
то, что в общем случае коэффициенты
разложения
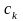 оказываются
коррелированными. При теоретических
исследованиях проще оперировать с
некоррелированными коэффициентами. В
этом случае задача отыскания функций
усложняется и сводится к решению
интегрального уравнения:
оказываются
коррелированными. При теоретических
исследованиях проще оперировать с
некоррелированными коэффициентами. В
этом случае задача отыскания функций
усложняется и сводится к решению
интегрального уравнения:
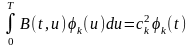 ,
(2.4.4)
,
(2.4.4)
связывающего
функции разложения с ФК СП
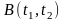 .
Представление СП в виде ряда (2.4.2) с
некоррелированными и имеющими нулевые
средние значения коэффициентами
называется каноническим разложением
или разложением Карунена - Лоэва.
.
Представление СП в виде ряда (2.4.2) с
некоррелированными и имеющими нулевые
средние значения коэффициентами
называется каноническим разложением
или разложением Карунена - Лоэва.
Для белого шума любая система ортогональных функций обеспечивает некоррелированность коэффициентов разложения.
В соответствии с (2.4.2) СП без постоянной составляющей можно представить в виде ряда Фурье:
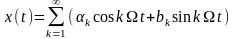 ,
(2.4.5)
,
(2.4.5)
коэффициенты которого случайные и, в общем случае, коррелированные величины. Для некоррелированности коэффициентов разложения в ряде Фурье необходимо выполнение одного из условий:
- случайный процесс периодичен с периодом Т;
- интервал разложения достаточно большой ;
- СП представляет собой белый шум.
Возведя обе части равенства (2.4.5) в квадрат и проинтегрировав на интервале от 0 до Т, с учетом ортогональности тригонометрических функций получим выражение:
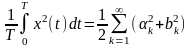 ,
(2.4.6)
,
(2.4.6)
аналогичное равенству Парсеваля, в котором обе части являются случайными величинами.
Если СП не содержит частот выше , то он может быть представлен в виде ряда Котельникова:
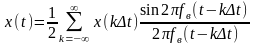 , (2.4.7)
, (2.4.7)
где
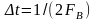 .
.
Если СП имеет
равномерную СПМ
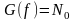 в полосе частот от минус
до плюс
,
то
в полосе частот от минус
до плюс
,
то
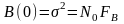 и
и
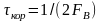 .
Следовательно, интервал времени
=
.
Следовательно, интервал времени
=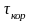 ,
а отсчеты представляют собой ближайшие
некоррелированные значения СП. При
использовании ряда Котельникова для
СП длительностью Т получим выражение,
аналогичное (2.4.6):
,
а отсчеты представляют собой ближайшие
некоррелированные значения СП. При
использовании ряда Котельникова для
СП длительностью Т получим выражение,
аналогичное (2.4.6):
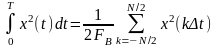 ,
(2.4.8)
,
(2.4.8)
где
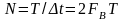 .
.
Лекция 2.5 Случайные последовательности
2.5.1 Марковские случайные процессы
Среди различных типов СП можно выделить некоторые процессы, которые полностью характеризуются простейшими плотностями вероятности. К ним относится так называемый абсолютно СП или белый шум. В этом процессе значения Х1, Х2, …, Хn, взятые в различные моменты t1, t2, ..., tn, статистически независимы друг от друга, как бы близко эти моменты ни располагались друг от друга. Следовательно, его совместная (двумерная) плотность вероятности (ПВ) равна произведению одномерных плотностей:
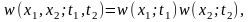
а многомерная:
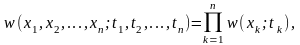
т.е. в рассматриваемом случае все n-мерные ПВ определяются одномерной ПВ.
Следующий по сложности процесс получается, когда вся информация о нём содержится в двумерной ПВ w(x1, x2; t1, t2). Такими являются гауссовские СП или простые марковские СП. Для определения ФК, МО и дисперсии гауссовского СП требуется знание лишь двумерной ПВ. Если все сечения гауссовского СП не коррелированны, то его n-мерная ПВ выражается через одномерные ПВ и имеет вид:
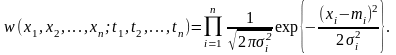
Это выражение
определяет условие статистической
независимости отдельных сечений СП.
Если гауссовские СВ Xi
при различных
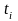 не коррелированны, то они также
статистически независимы.
не коррелированны, то они также
статистически независимы.
Отличительной особенностью простого марковского СП является минимальное последействие: для него вероятность нахождения СП X(t) в заданном интервале значений в момент tn зависит только от состояния в предшествующий момент tn-1:
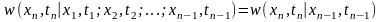 ,
,
т.е. n-мерная ПВ простого марковского СП при t1 < t2 < t3 < … < tn полностью определяется двумерной ПВ.
При некоторых дополнительных условиях переходная ПВ при t2 > t1 удовлетворяет дифференциальному уравнению 2-го порядка в частных производных:
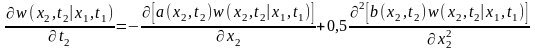 (2.5.1)
(2.5.1)
при начальном
условии
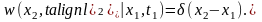 Здесь a(x2,
t2) –коэффициент
сноса, а b(х2,
t2) – коэффициент
диффузии. Данное уравнение (2.5.1) называют
уравнением Фоккера-Планка-Колмогорова.
Марковские процессы, удовлетворяющие
этому уравнению, называют диффузионными.
В зависимости от вида коэффициентов
a и b
диффузионный марковский процесс
может иметь различные распределения
вероятностей.
Здесь a(x2,
t2) –коэффициент
сноса, а b(х2,
t2) – коэффициент
диффузии. Данное уравнение (2.5.1) называют
уравнением Фоккера-Планка-Колмогорова.
Марковские процессы, удовлетворяющие
этому уравнению, называют диффузионными.
В зависимости от вида коэффициентов
a и b
диффузионный марковский процесс
может иметь различные распределения
вероятностей.
К марковским процессам относятся также процессы с независимыми приращениями. Свойством таких систем является взаимная независимость разности значений процесса X(t2) – X(t1), X(t3) – X(t2), ... , X(tn) – X(tn-1) для любой совокупности моментов времени t1 < t2 <… < tп (n ≥ 3). Для определения функции распределения любого порядка для такого процесса достаточно знать только одномерные распределения X(t) и X(tk) – X(tk-1), т.е. одномерную и двумерную функции распределения процесса. Если распределение приращений X(t) – X(t - τ) зависит только от τ, то процесс с независимыми приращениями называется однородным.
В зависимости от того, непрерывное или дискретное множество значений принимают СВ x(t) и её параметр t в области задания процесса [0, Т], различают четыре основных вида марковских СП: марковские цепи (дискретный процесс с дискретным временем), марковские последовательности (непрерывный процесс с дискретным временем), дискретный марковский процесс (дискретный процесс с непрерывным временем) и непрерывнозначный марковский процесс (непрерывный процесс с непрерывным временем). Характер временных реализаций перечисленных процессов показан в табл. 2.5.1. Помимо четырех основных видов, возможны другие, более сложные процессы марковского типа (дискретно-непрерывные, различного характера смешанные и т. д.).
Таблица 2.5.1 – Классификация Марковских процессов
-
Значение
аргумента
Значения процесса
Дискретные
Непрерывные
Дискретные
Цепь Маркова
Марковская
последовательность
Непрерывные
Дискретный
марковский процесс
Непрерывный
марковский процесс
Эволюция вероятности
перехода
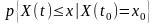 марковских процессов описывается
уравнением вида:
марковских процессов описывается
уравнением вида:
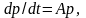 (2.5.2)
(2.5.2)
где A – некоторый линейный оператор (матрица, дифференциальный оператор и др.). Это позволяет исследовать поведение марковских процессов при помощи методов решения соответствующих дифференциальных уравнений. При этом характер решаемых физических задач может быть различным, в зависимости от заданных начальных и граничных условий для уравнения (2.5.2).
2.5.2 Винеровский процесс
Основополагающую роль при формировании более сложных марковских процессов играет винеровский процесс (ВП). Этот процесс был введён Н. Винером в качестве простой модели броуновского движения частицы, передвигающейся под воздействием множества соударений таких же частиц. ВП H(t) определяется как интеграл от нормального белого шума N(t):
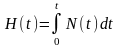 (2.5.3)
(2.5.3)
или с помощью
стохастического дифференциального
уравнения
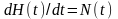 ,
где N(t)
– гауссовский стационарный СП с
нулевым МО и δ-корреляцией:
,
где N(t)
– гауссовский стационарный СП с
нулевым МО и δ-корреляцией:
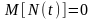 ,
,
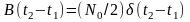 .
Поскольку последнее преобразование
(2.5.3) является линейным, то ВП остается
гауссовским. Одномерная ПВ ВП H(t),
его МО, дисперсия и ФК равны:
.
Поскольку последнее преобразование
(2.5.3) является линейным, то ВП остается
гауссовским. Одномерная ПВ ВП H(t),
его МО, дисперсия и ФК равны:
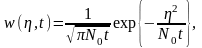 t
≠ 0,
t
≠ 0,
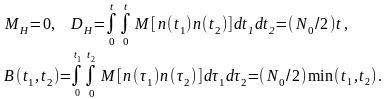
ВП является
нестационарным с дисперсией
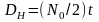 ,
пропорциональной времени; т.е. его
реализации имеют возрастающий во времени
разброс траекторий. Для ВП коэффициент
сноса в (2.5.3) a(η, t)
= 0, а коэффициент диффузии b(η,
t) = N0/2
= const; поэтому ВП часто
называют диффузионным. Важной
особенностью ВП является то, что его
реализации нигде не дифференцируемы,
хотя являются непрерывными с вероятностью
единица. Это следствие особых свойств
ВП H(t),
производная от которого N(t)
не существует.
,
пропорциональной времени; т.е. его
реализации имеют возрастающий во времени
разброс траекторий. Для ВП коэффициент
сноса в (2.5.3) a(η, t)
= 0, а коэффициент диффузии b(η,
t) = N0/2
= const; поэтому ВП часто
называют диффузионным. Важной
особенностью ВП является то, что его
реализации нигде не дифференцируемы,
хотя являются непрерывными с вероятностью
единица. Это следствие особых свойств
ВП H(t),
производная от которого N(t)
не существует.
Марковские диффузионные процессы являются во многих случаях удобной математической моделью сообщений, сигналов и помех.
2.5.3 Представление случайных процессов дифференциальными уравнениями
Для описания сообщений, сигналов и помех можно воспользоваться их представлением в пространстве состояний. В зависимости от вида воздействий дифференциальные уравнения, определяющие поведение процесса в этом пространстве, могут быть детерминированными или стохастическими.
Для непрерывного времени задание состояния процесса (или системы) во времени означает задание функции (вектора состояния):
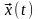 =
[x1(t),
x2(t),
…, xn(t)]T,
=
[x1(t),
x2(t),
…, xn(t)]T,
где Т – знак транспонирования матрицы.
Проведение многих реальных динамических систем хорошо описывается стохастическим векторным дифференциальным уравнением вида:
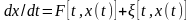 ,
(2.5.4)
,
(2.5.4)
где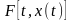 – n-мерная неслучайная
вектор-функция своих аргументов;
– n-мерная неслучайная
вектор-функция своих аргументов;
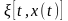 – n-мерный СП с
известными вероятностными характеристиками,
которые могут зависеть от вектора
.
В частности, если в этом выражении
(2.5.4)
является белым гауссовским шумом,
то вектор состояния
представляет
собой простой марковский процесс
соответствующей размерности. Важнейшим
свойством такого процесса является то,
что при фиксированном настоящем (сечении
t0), его
будущее состояние не зависит от прошлого
(значений процесса при t
< t0).
– n-мерный СП с
известными вероятностными характеристиками,
которые могут зависеть от вектора
.
В частности, если в этом выражении
(2.5.4)
является белым гауссовским шумом,
то вектор состояния
представляет
собой простой марковский процесс
соответствующей размерности. Важнейшим
свойством такого процесса является то,
что при фиксированном настоящем (сечении
t0), его
будущее состояние не зависит от прошлого
(значений процесса при t
< t0).
2.5.4 Модели источников сообщений, сигналов, помех
В задачах синтеза СП можно представить на основе описания поведения динамической порождающей системы (рис. 2.5.1, а), на вход которой воздействует белый шум N(t), а на выходе формируется процесс X(t) с требуемыми характеристиками.
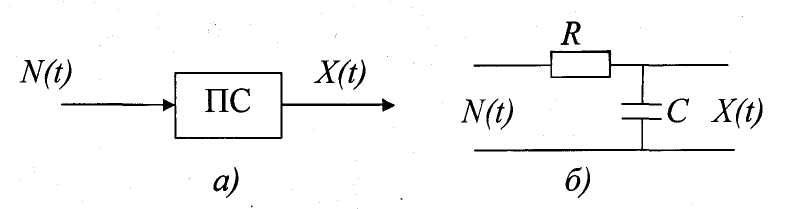
Рисунок 2.5.1 – Порождающая система (фильтр) (а) и динамическая система 1-го порядка (б)
В теории статистической
радиотехники доказано, что ФК процесса
 на выходе системы и взаимная ФК процессов
на входе
на выходе системы и взаимная ФК процессов
на входе
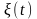 и на выходе
линейной системы, на вход которой
подается белый шум с равномерным
энергетическим спектром
и на выходе
линейной системы, на вход которой
подается белый шум с равномерным
энергетическим спектром
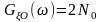 и ФК Bξ(τ)
=
и ФК Bξ(τ)
=
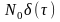 ,
соответственно равны:
,
соответственно равны:
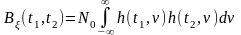 ,
,
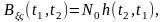
где
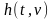 – ИХ линейной системы.
– ИХ линейной системы.
Из второго выражения
следует простой корреляционный метод
определения ИХ
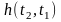 линейной системы: если на вход системы
подается белый шум, то при N0
= 1 взаимная ФК процессов на входе в
точности совпадает с ИХ
.
линейной системы: если на вход системы
подается белый шум, то при N0
= 1 взаимная ФК процессов на входе в
точности совпадает с ИХ
.
Из первого выражения
следует, что стационарный в широком
смысле СП
с ФК
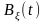 можно рассматривать как реакцию на
воздействие белого шума единичной
интенсивности линейной системы с ИХ
можно рассматривать как реакцию на
воздействие белого шума единичной
интенсивности линейной системы с ИХ
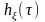 ,
удовлетворяющей интегральному уравнению:
,
удовлетворяющей интегральному уравнению:
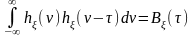 .
.
Такую линейную
систему называют формирующим
фильтром. Реакцию
на выходе произвольной линейной системы
с ИХ на воздействие процесса
можно рассматривать как реакцию на
входной белый шум
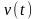 линейной системы, представляющей
последовательное соединение формирующего
фильтра и данной линейной системы (рис.
2.5.2, а):
линейной системы, представляющей
последовательное соединение формирующего
фильтра и данной линейной системы (рис.
2.5.2, а):
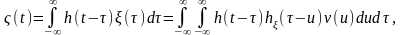
или как реакцию на воздействие белого шума линейной системы с ИХ (рис. 2.5.2, б):
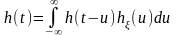 .
.
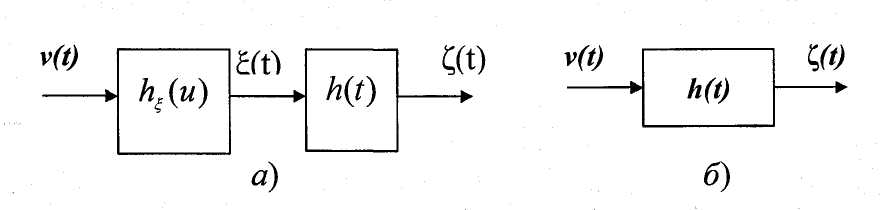
система (б)
Лекция 2.6 Комплексное и квазигармоническое представление узкополосных случайных процессов
2.6.1 Узкополосные процессы. Преобразование Гильберта
В общем случае
сигналы связи можно подразделить на
радио- и видеосигналы. Спектр видеосигнала
сосредоточен в области низких частот.
Радиосигналы обычно представляют собой
узкополосный процесс, отличительной
особенностью которого является наличие
резко выраженного максимума СПМ вблизи
некоторой частоты
,
отличной от нуля. Условие узкополосности
представляется неравенством
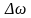 <<
,
– ширина спектра.
<<
,
– ширина спектра.
В общем случае при произвольном виде модуляции радиосигнал можно представить в форме:
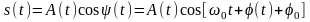 ,
(2.6.1)
,
(2.6.1)
где функции
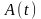 и
и
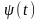 называются соответственно огибающей
и фазой радиосигнала.
Возникающей при представлении сигналов
в данном виде неопределённости в выборе
функций
и
можно
избежать при представлении огибающей
называются соответственно огибающей
и фазой радиосигнала.
Возникающей при представлении сигналов
в данном виде неопределённости в выборе
функций
и
можно
избежать при представлении огибающей
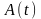 и фазы
с помощью следующих соотношений:
и фазы
с помощью следующих соотношений:
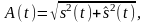
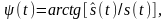 (2.6.2)
(2.6.2)
где
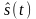 – новая функция, связанная с исходной
функцией соотношениями:
– новая функция, связанная с исходной
функцией соотношениями:
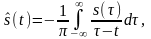
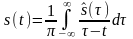 .
(2.6.3)
.
(2.6.3)
Эти
соотношения называются преобразованиями
Гильберта,
а функция
– функцией,
сопряжённой по Гильберту функции
.
В соответствии с последними выражениями
рассматриваемая функция
представлена в виде проекции вектора
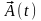 на ось абсцисс, относительно которой
отсчитывается угол
(рис. 2.6.1).
на ось абсцисс, относительно которой
отсчитывается угол
(рис. 2.6.1).
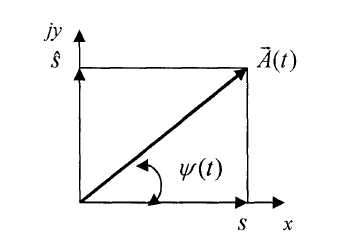 Рисунок
2.6.1 – Геометрическое представление
сигнала
Рисунок
2.6.1 – Геометрическое представление
сигнала
Основные свойства огибающей , вытекающие непосредственно из выражения (2.6.2) и справедливые при любой функции :
1) в точках, где
функция
равна нулю, имеет место равенство
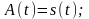
2) дифференцируя получим:
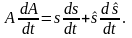
Отсюда следует
дополнительное равенство:
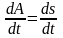 при
=
0, когда
при
=
0, когда
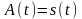 .
Следовательно, в точках, в которых
=
0, кривые
и
имеют общие касательные;
.
Следовательно, в точках, в которых
=
0, кривые
и
имеют общие касательные;
3) для того, чтобы можно было рассматривать как «простейшую» огибающую быстро осциллирующей функции , необходимо чтобы кривая касалась кривой в точках, в которых имеет амплитудное или близкое к нему значение, т.е. в точках, где = 0, функция должна принимать значения, близкие к амплитудным. Это условие обеспечивается, если функция является сопряжённой по Гильберту функции .
Перейдя в выражении
(2.6.3) к новой переменной
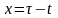 с учётом
с учётом
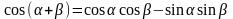 ,
найдём сопряжённую функцию
для
,
найдём сопряжённую функцию
для
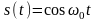 :
:
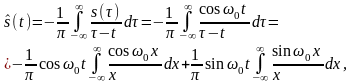
где
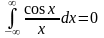 и
и
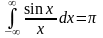 (в смысле главного значения).
(в смысле главного значения).
Следовательно,
функции
соответствует сопряжённая функция
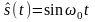 ,
которая проходит через нуль в моменты,
когда исходная функция проходит через
максимум. Аналогичным образом функции
,
которая проходит через нуль в моменты,
когда исходная функция проходит через
максимум. Аналогичным образом функции
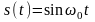 соответствует сопряжённая функция
соответствует сопряжённая функция
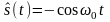 .
Подставляя
и
в выражение (2.6.2), получим для огибающей
гармонического колебания общепринятое
выражение
.
Подставляя
и
в выражение (2.6.2), получим для огибающей
гармонического колебания общепринятое
выражение
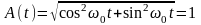 .
Аналогичный результат получается и для
и
.
Аналогичный результат получается и для
и
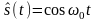 .
.
Таким образом, выражение (2.6.2) определяет огибающую в виде линии, касательной к точкам максимума исходной функции, и, в случае гармонического колебания, соединяющей два соседних максимума кратчайшим путём – прямой линией. Это свойство выражения (2.6.2) сохраняется и для сложного сигнала, если выполняется условие медленности изменения огибающей, т. е. если речь идет об узкополосном сигнале.
Если исходный сигнал представляет собой сумму спектральных составляющих:
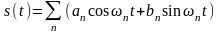 ,
(2.6.4)
,
(2.6.4)
то сопряженная функция равна:
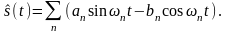 (2.6.5)
(2.6.5)
Ряд (2.6.5) называется рядом, сопряженным ряду (2.6.4).
Если сигнал представлен интегралом Фурье:
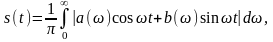 (2.6.6)
(2.6.6)
то функция может быть представлена в виде интеграла:
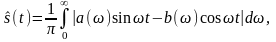 (2.6.7)
(2.6.7)
сопряжённого интегралу (2.6.6).
При преобразовании
гармонического колебания по Гильберту
его амплитуда остается неизменной,
следовательно, по модулю спектральные
плотности
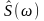 сопряженной функции
и
сопряженной функции
и
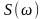 исходной
функции s(t)
равны, а фазовые характеристики
отличаются. Из сопоставления выражений
(2.6.6) и (2.6.7) непосредственно вытекает,
что все спектральные составляющие
функции
отстают по фазе на 90° от соответствующих
составляющих функции s(t).
Следовательно, в областях положительных
и отрицательных частот спектральные
плотности
и
связаны соотношениями:
исходной
функции s(t)
равны, а фазовые характеристики
отличаются. Из сопоставления выражений
(2.6.6) и (2.6.7) непосредственно вытекает,
что все спектральные составляющие
функции
отстают по фазе на 90° от соответствующих
составляющих функции s(t).
Следовательно, в областях положительных
и отрицательных частот спектральные
плотности
и
связаны соотношениями:
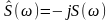 ,
,
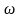 >
0, (2.6.8)
>
0, (2.6.8)
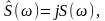 <
0. (2.6.9)
<
0. (2.6.9)
Вследствие изменения фазовой характеристики сопряженная функция по своей форме может сильно отличаться от исходной функции s(t).
Мгновенная частота узкополосного сигнала равна:
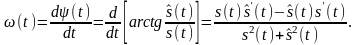 (2.6.10)
(2.6.10)
Выделив в частоте
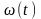 постоянную
часть
,
можно написать выражение для
постоянную
часть
,
можно написать выражение для
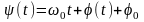 ,
в котором
,
в котором
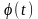 не содержит слагаемого, линейно
зависящего от времени. Тем самым
устраняется произвол в выборе «средней
частоты» сигнала
и соответственно функции
.
не содержит слагаемого, линейно
зависящего от времени. Тем самым
устраняется произвол в выборе «средней
частоты» сигнала
и соответственно функции
.
2.6.2 Огибающая и фаза случайного процесса
Высокочастотное
колебание s(t),
определяемое выражением (2.6.1), с учётом
,
при
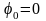 можно представить в виде суммы двух
квадратурных колебаний:
можно представить в виде суммы двух
квадратурных колебаний:
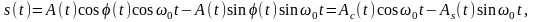 (2.6.11)
(2.6.11)
где
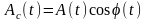 и
и
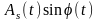 – амплитуды соответственно косинусной
и синусной составляющих колебания
,
причём:
– амплитуды соответственно косинусной
и синусной составляющих колебания
,
причём:
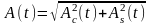 ;
;
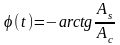 .
(2.6.12)
.
(2.6.12)
Для отыскания ПВ
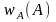 и
и
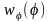 требуется знание соответствующих
ПВ
требуется знание соответствующих
ПВ
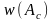 и
и
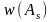 ,
а также совместной ПВ
,
а также совместной ПВ
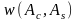 .
ПВ
и
можно определить, сопоставив
.
ПВ
и
можно определить, сопоставив
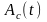 или с
:
или с
:
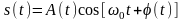 ;
.
Отличие
от
заключается в исключении слагаемого
;
.
Отличие
от
заключается в исключении слагаемого
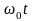 из аргумента косинуса, что означает
сдвиг всего спектра каждой из реализаций
СП на величину
в направлении нулевой частоты. При этом
сохраняется закон распределения СП
.
Поэтому, если процесс
нормальный, то и процесс
нормальный (оба СП с нулевым средним).
Среднее значение квадрата огибающей
равно:
из аргумента косинуса, что означает
сдвиг всего спектра каждой из реализаций
СП на величину
в направлении нулевой частоты. При этом
сохраняется закон распределения СП
.
Поэтому, если процесс
нормальный, то и процесс
нормальный (оба СП с нулевым средним).
Среднее значение квадрата огибающей
равно:
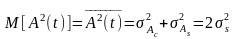 .
(2.6.13)
.
(2.6.13)
Одномерные ПВ СФ
и
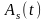 определяются выражениями:
определяются выражениями:
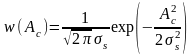 ;
;
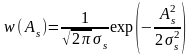 .
(2.6.14)
.
(2.6.14)
Взаимная ФК между
СП
и
при
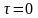
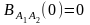 .
Следовательно,
и
в один и тот же момент времени являются
независимыми величинами. Поэтому
совместная
и двумерная ПВ
.
Следовательно,
и
в один и тот же момент времени являются
независимыми величинами. Поэтому
совместная
и двумерная ПВ
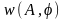 определяются выражениями:
определяются выражениями:
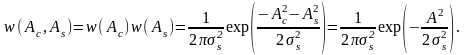 (2.6.15)
(2.6.15)
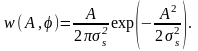 (2.6.16)
(2.6.16)
ПВ начальной фазы равна:
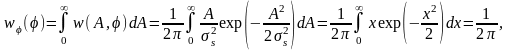
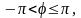 (2.6.17)
(2.6.17)
где
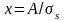 .
.
Таким образом, начальная фаза узкополосного СП распределена равномерно на отрезке [0, 2π].
Интегрируя по
переменной
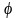 ,
получаем одномерную ПВ:
,
получаем одномерную ПВ:
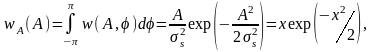 0 < А < ∞.
(2.6.18)
0 < А < ∞.
(2.6.18)
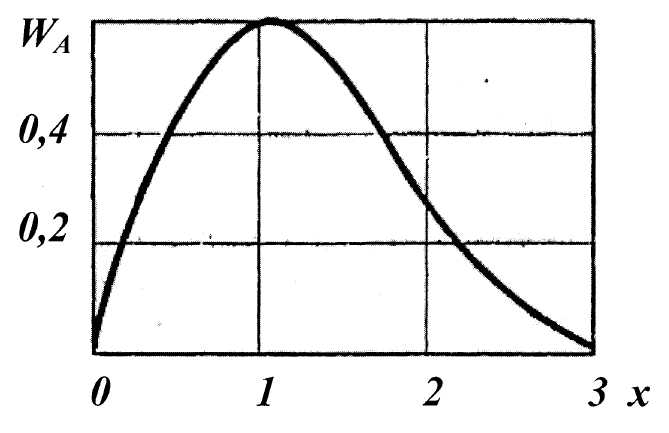
Данное распределение огибающей называется распределением Рэлея (рис. 2.6.2).
 Рисунок
2.6.2 – График распределения Рэлея
Рисунок
2.6.2 – График распределения Рэлея
Максимум значения
функция
достигает при
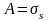 (х = 1) (наивероятнейшее значение
огибающей). Среднее значение (математическое
ожидание) огибающей равно:
(х = 1) (наивероятнейшее значение
огибающей). Среднее значение (математическое
ожидание) огибающей равно:
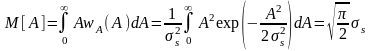 .
(2.6.19)
.
(2.6.19)
Аналогично:
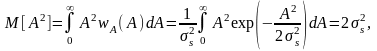 (2.6.20)
(2.6.20)
т.е. средняя мощность огибающей равна удвоенной дисперсии исходного физического сигнала.
Вероятность того, что огибающая превысит некоторый заданный уровень С, определяется формулой:
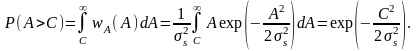 (2.6.21)
(2.6.21)
Из этой формулы
следует, что уже при
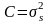 вероятность его превышения составляет
всего лишь примерно 1%. Поэтому можно
считать, что ширина дорожки, фактически
наблюдаемой на экране осциллографа, не
превышает (5-6)
вероятность его превышения составляет
всего лишь примерно 1%. Поэтому можно
считать, что ширина дорожки, фактически
наблюдаемой на экране осциллографа, не
превышает (5-6)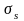 .
.
ФК огибающей узкополосного нормального процесса определяется по формуле:
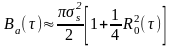 .
(2.6.22)
.
(2.6.22)
где
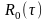 – коэффициент корреляции, представляет
собой огибающую нормированной ФК СП
s(t),
т.е. функции, определяемой выражением
(при
– коэффициент корреляции, представляет
собой огибающую нормированной ФК СП
s(t),
т.е. функции, определяемой выражением
(при
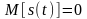 ):
):
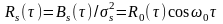 .
(2.6.23)
.
(2.6.23)
Представим в виде произведения:
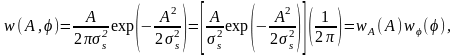
откуда непосредственно следует независимость СВ А(t) и при их отсчёте в один и тот же момент времени.
Из полученных для
и
соотношений следует общее заключение:
СП
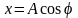 ,
в котором А и
независимые СВ, причём А распределена
по закону Рэлея, а
– равновероятна в интервале
,
в котором А и
независимые СВ, причём А распределена
по закону Рэлея, а
– равновероятна в интервале
 ,
обладает нормальной ПВ. При этом условие
узкополосности процесса
не обязательно; необходимо лишь,
чтобы А и
были связаны соотношением (2.6.26).
,
обладает нормальной ПВ. При этом условие
узкополосности процесса
не обязательно; необходимо лишь,
чтобы А и
были связаны соотношением (2.6.26).
ФК фазы определяется выражением:
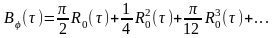 (2.6.24)
(2.6.24)
При
ряд сходится к
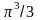 ,
т.е. дисперсия фазы
,
т.е. дисперсия фазы
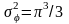 .
.
2.6.3 Функция корреляции узкополосного случайного процесса
По теореме Винера
– Хинчина ФК стационарного СП Х(t),
односторонний спектр мощности которого
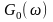 концентрируется в окрестности
некоторой частоты
>
0:
концентрируется в окрестности
некоторой частоты
>
0:
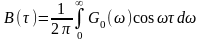 .
(2.6.25)
.
(2.6.25)
Для СП с симметричным
относительно центральной частоты
спектром
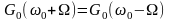 :
:
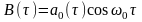 ,
(2.6.26)
,
(2.6.26)
где коэффициент
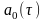 играет роль огибающей, изменяющейся
медленно по сравнению с множителем
играет роль огибающей, изменяющейся
медленно по сравнению с множителем
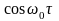 .
Введя нормированную огибающую
.
Введя нормированную огибающую
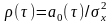 ,
получим:
,
получим:
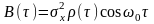 .
(2.6.27)
.
(2.6.27)
Интервал корреляции узкополосного СП определяется по формуле:
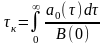 .
(2.6.28)
.
(2.6.28)
Типичная корреляционная функция узкополосного СП представлена на рис. 2.6.3.
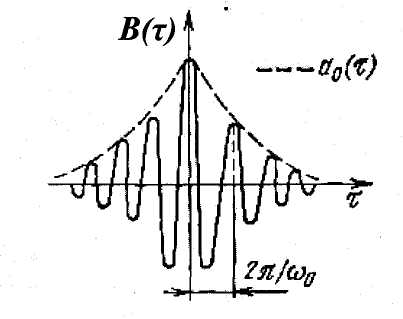
Рисунок 2.6.3 – ФК узкополосного СП
2.6.4 Комплексный (аналитический) сигнал
В радиотехнике принято представлять гармоническое колебание в форме:
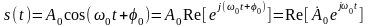 (2.6.29)
(2.6.29)
или
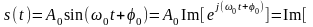
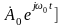 ,
(2.6.30)
,
(2.6.30)
где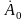 =
=
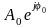 – комплексная амплитуда.
– комплексная амплитуда.
Часто символы Re и Im опускают и пишут просто:
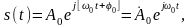 (2.6.
31)
(2.6.
31)
подразумевая действительную или мнимую часть этого выражения.
Представление колебаний в комплексной форме может быть распространено на негармонические колебания. Физическому сигналу, представленному действительной функцией , соответствует комплексный или аналитический сигнал:
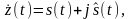 (2.6.32)
(2.6.32)
где – функция, сопряжённая по Гильберту сигналу .
Сигналу , где огибающая определена соотношением (2.6.2), соответствуют сопряженная функция:
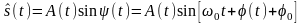 (2.6.33)
(2.6.33)
и аналитический сигнал:
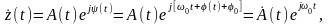 (2.6.34)
(2.6.34)
где
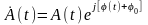 – комплексная огибающая узкополосного
сигнала.
– комплексная огибающая узкополосного
сигнала.
Модуль комплексной
огибающей, равный
(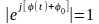 при
любом законе изменения
),
содержит информацию только об амплитудной
модуляции сигнала, а фазовый множитель
при
любом законе изменения
),
содержит информацию только об амплитудной
модуляции сигнала, а фазовый множитель
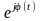 –
только об угловой модуляции. В целом
произведение
–
только об угловой модуляции. В целом
произведение
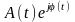 содержит полную информацию о сигнале
(за
исключением несущей частоты
,
которая предполагается известной). Это
свойство комплексной огибающей,
позволяющее при анализе узкополосных
сигналов исключать из рассмотрения
частоту
,
придает важное значение понятию
«аналитический сигнал».
содержит полную информацию о сигнале
(за
исключением несущей частоты
,
которая предполагается известной). Это
свойство комплексной огибающей,
позволяющее при анализе узкополосных
сигналов исключать из рассмотрения
частоту
,
придает важное значение понятию
«аналитический сигнал».
Основные свойства аналитического сигнала и комплексной огибающей.
1) Произведение
аналитического сигнала
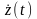 на сопряжённый
ему сигнал
на сопряжённый
ему сигнал
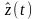 равно квадрату
огибающей исходного сигнала
:
равно квадрату
огибающей исходного сигнала
:
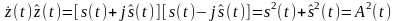 .
(2.6.35)
.
(2.6.35)
Модуль аналитического
сигнала
равен просто огибающей сигнала
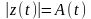 .
.
2) Спектр аналитического сигнала содержит только положительные частоты.
Спектральная
плотность
 аналитического
сигнала
определяется
суммой
аналитического
сигнала
определяется
суммой
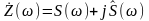 .
Но при
> 0
.
Но при
> 0
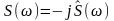 и при
< 0
и при
< 0
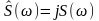 .
Следовательно:
.
Следовательно:
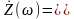 (2.6.36)
(2.6.36)
Интеграл Фурье для аналитического сигнала имеет вид:
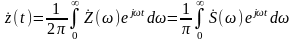 ,
(2.6.37)
,
(2.6.37)
где
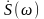 – спектральная плотность исходного
сигнала
.
– спектральная плотность исходного
сигнала
.
3) Спектральная
плотность комплексной огибающей
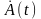 совпадает со смещённой на величину
влево (в область нижних частот) спектральной
плотностью аналитического сигнала
.
совпадает со смещённой на величину
влево (в область нижних частот) спектральной
плотностью аналитического сигнала
.
Исходя из определения спектральной плотности, запишем:
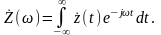
Подставив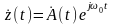 ,
получим:
,
получим:
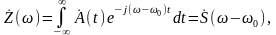 >
0. (2.6.38)
>
0. (2.6.38)
4) ФК аналитического сигнала, определяемая выражением:
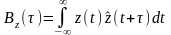 ,
(2.6.39)
,
(2.6.39)
связана с ФК исходного физического узкополосного сигнала и его огибающей соотношениями:
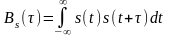 (2.6.40)
(2.6.40)
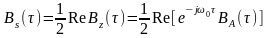 . (2.6.41)
. (2.6.41)
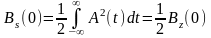 .
(2.6.42)
.
(2.6.42)
Из этого выражения
следует, что энергия аналитического
сигнала
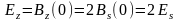 равна удвоенной энергии исходного
физического сигнала.
равна удвоенной энергии исходного
физического сигнала.
Выводы по теме 2
Сообщения, сигналы и помехи в системах электрической связи описываются функциями времени, которые являются детерминированными или случайными.
Любую непрерывную функцию, удовлетворяющую условиям Дирихле, можно представить обобщенным рядом Фурье. Частным случаем обобщенного ряда Фурье является обычный ряд Фурье для периодических функций, когда в качестве базисных используются гармонические функции кратных частот.
Периодическая функция времени имеет линейчатый дискретный спектр. Спектр непериодической функции времени – сплошной. Он определяется спектральной плотностью. Модуль спектральной плотности определяет амплитудный спектр сигнала, а аргумент – фазовый спектр.
Сигнал х(t) c финитным (ограниченным) спектром FВ представляется в обобщенный ряд по базисной системе функций
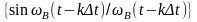 –
ряд Котельникова. Коэффициенты ряда
– это отсчеты сигнала х(kΔt)
в точках, кратных интервалу дискретизации
Δt
≤ 1/2 FВ.
–
ряд Котельникова. Коэффициенты ряда
– это отсчеты сигнала х(kΔt)
в точках, кратных интервалу дискретизации
Δt
≤ 1/2 FВ.СП чаще всего описываются косвенным путём через ПВ и ИФР.
Непрерывные источники случайных сигналов могут описываться не только косвенным способом (через функции распределения и моментные функции), но и прямым способом (через стохастические дифференциальные уравнения состояния).
Более простыми характеристиками СП являются его математическое ожидание, дисперсия и ФК.
В теории и практике электросвязи большую роль играют стационарные СП, определяемые не зависящей от времени одномерной ПВ и двумерной ПВ, зависящей от разности выбранных сечений τ.
Непрерывные и дискретные источники сообщений, сигналов и помех можно описать как прямым способом (через временные функции их реализаций), так и косвенным способом (через различные спектральные характеристики, а для СП – через функции распределения).
Основные числовые характеристики сигналов: энергия, мощность, уровни сигналов, динамический диапазон, коэффициент амплитуды, длительность, ширина спектра.
Множество величин, однозначно определяющих поведение канала (системы, цепи) в некоторый момент t, содержащее минимальное число элементов п, называют состоянием, а сами элементы этого множества (вектор состояния) – переменными состояния. Для любой заданной цепи можно составить два уравнения, позволяющих по состоянию в момент t0 и сигналу, поступающему на вход, найти состояние в момент t > t0 и выходной сигнал. Первое из них называется уравнением состояния, а второе — уравнением наблюдения. Уравнение состояния обычно задают в виде системы дифференциальных уравнений первого порядка (векторного уравнения первого порядка).
Важной особенностью метода переменных состояния является возможность непосредственного моделирования систем, описываемых уравнениями состояния с помощью аналогового или цифрового вычислительного устройства (т.е. можно получить решение формализируемой задачи). Но более важно, что метод позволяет по наблюдаемому процессу оценить сообщение, передаваемое сигналом.
Одно из приложений метода переменных состояния – возможность смоделировать любой случайный процесс (на выходе источника сообщений, отдельных звеньев канала и т.д.) как отклик некоторой динамической системы (описываемой системой дифференциальных уравнений), на вход которой воздействует стационарный центрированный гауссовский δ-коррелированный процесс. Смоделированный процесс оказывается марковским.
Контрольные вопросы по теме 2
В чём суть прямого и косвенного описания сигналов?
Назовите способы динамического представления сигналов и объясните их суть.
В чём суть фильтрующего свойства - функции?
Напишите выражение для сигнала в трёхмерном и многомерном векторном пространстве. Объясните суть такой записи.
Дайте определение линейно независимого множества.
Каковы основные свойства Евклидова пространства, пространств Гильберта и Хэмминга?
Дайте определение непрерывных и дискретных сигналов.
Какие функции называются ортогональными?
Запишите ряд Фурье в общем виде.
Что такое спектр сигнала?
Запишите выражение для спектра периодического сигнала.
Рассчитайте амплитуды гармонических составляющих для периодической последовательности прямоугольных импульсов.
Что такое ширина спектра сигнала?
Чему равна ширина спектра последовательности импульсов?
Запишите выражение для спектра непериодического сигнала.
Рассчитайте и постройте спектр одиночного прямоугольного импульса.
Какие параметры сигнала влияют на ширину спектра и на частоту гармонических составляющих спектра?
18. Сформулируйте теорему Котельникова.
19. Рассчитайте и постройте спектр дискретизированного сигнала.
Рассчитайте и постройте спектр сигнала АИМ.
Как восстановить непрерывный сигнал из отсчетов?
Чем определяются погрешности дискретизации и восстановления сигналов?
Какой процесс называется случайным?
Что такое ПВ и ИФР? Как они связаны?
Запишите выражения для числовых характеристик СП.
Какой процесс называется нормальным?
Какой процесс называется узкополосным?
Дайте определение ФКСП.
Запишите выражение для ФК стационарного, эргодического СП с нулевым средним.
Нарисуйте стандартный вид графика для ФК.
Чему равно максимальное значение ФК СП?
Каков физический смысл ФК?
Как определить интервал корреляции СП?
Что такое коэффициент корреляции СП?
35. Рассчитайте энергетический спектр СП, если известна его ФК.
36. Что такое белый шум?
Список литературы по теме 2
1. Теория электрической связи: Учебник для вузов /Зюко А.Г., Кловский Д.Д., Коржик В.И., Назаров М.В. - М.: Радио и связь, 1999. – 432 с.
2. Гоноровский И.С. Радиотехнические цепи и сигналы. - М.: Радио и связь, 1986. – 512 с.
3. Баскаков С.И. Радиотехнические цепи и сигналы. Учебник для вузов. – М.: Высш. шк., 2005. – 462 с.
4. Френкс Л. Теория сигналов / Пер. с англ. под ред. Д.Е. Вакмана. – М.: Сов. Радио, 1974. – 344 с.
5. Левин Б.Р. Теоретические основы статистической радиотехники. – 3-е изд., перераб. и доп. - М.: Радио и связь, 1989. – 656 с.
6. Тихонов В. И. Статистическая радиотехника. – М.: Радио и связь, 1982.
7. Большаков И. А., Гуткин Л. С., Левин Б. Р., Стратонович Р. Д. Математические основы современной радиоэлектроники. – М.: Сов.радио, 1968. – 208 с.
8. Гуткин Л. С. Современная радиоэлектроника м её проблемы. – М.: Сов.радио, 1980. – 192 с.
9. Скляр, Бернард. Цифровая связь. Теоретические основы и практическое применение. Пер с англ. – М.: Издательский дом «Вильямс», 2004. – 1104 с.