30. Бесконечно малые и бесконечно большие функции

Определение. Функция y = (x) называется бесконечно малой при х а, если lim (x) = 0. Функция y = f(x) называется бесконечно большой при х а (limf(x) = ), если становится больше любого наперед заданного числа или, если для любого числа М > 0 существует такое число , зависящее только от М, что из неравенства 0 < |x – a| < следует неравенство |f(x)| > M.

Теорема. Функция обратная к бесконечно малой является бесконечно большой и наоборот.

Действительно, если бесконечно малая функция (х) при х а оказывается в знаменателе дроби, то дробь неограниченно возрастает и становится бесконечно большой функцией 1/ (х) при х а.

36) Общие правила раскрытия неопределенностей

Раскрытие неопределённостей — методы вычисления пределов функций, заданных формулами, которые в результате формальной подстановки в них предельных значений аргумента теряют смысл, то есть переходят в выражения типа:

по которым невозможно судить о том, существуют или нет искомые пределы, не говоря уже о нахождении их значений, если они существуют.

Самым мощным методом является правило Лопиталя, однако и оно не во всех случаях позволяет вычислить предел. К тому же напрямую оно применимо только ко второму и третьему из перечисленных видов неопределённостей, то есть отношениям, и чтобы раскрыть другие типы, их надо сначала привести к одному из этих.

Также для вычисления пределов часто используется разложение выражений, входящих в исследуемую неопределённость, в ряд Тейлора в окрестности предельной точки.

Для раскрытия неопределённостей видов  ,  ,   пользуются следующим приёмом: находят предел (натурального) логарифма выражения, содержащего данную неопределённость. В результате вид неопределённости меняется. После нахождения предела от него берут экспоненту.

Для раскрытия неопределённостей типа   используется следующий алгоритм:

1. Выявление старшей степени переменной;

2. Деление на эту переменную как числителя, так и знаменателя.

Для раскрытия неопределённостей типа   существует следующий алгоритм:

1. Разложение на множители числителя и знаменателя;

2. Сокращение дроби.

Для раскрытия неопределённостей типа   иногда удобно применить следующее преобразование:

Пусть   и 

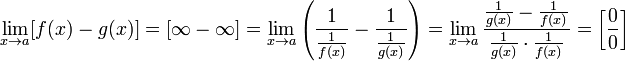
37) Опр. Средней скорости движения, мгновенной скорости, производной от функции. Алгебраический, физический, геометрический смысл производной.

Средняя (путевая) скорость — это отношение длины пути, пройденного телом, ко времени, за которое этот путь был пройден:

Средняя путевая скорость, в отличие от мгновенной скорости не является векторной величиной.

Средняя скорость равна среднему арифметическому от скоростей тела во время движения только в том случае, когда тело двигалось с этими скоростями одинаковые промежутки времени.

Мгновенная скорость есть первая производная пути по времени =  v=(ds/dt)=s'  где символы d/dt или штрих справа вверху у функции обозначают производную этой функции.  Иначе - это скорость v =s/t при t, стремящимся к нулю... :)  При отсутствии ускорения в момент измерения - мгновенная равна средней за время периода движения без ускорений Vмгн. = Vср. =S/t за этот период.

Произво́дная (функции в точке) — основное понятие дифференциального исчисления, характеризующее скорость изменения функции (в данной точке). Определяется как предел отношения приращения функции к приращению ее аргумента при стремлении приращения аргумента к нулю, если такой предел существует. Функцию, имеющую конечную производную (в некоторой точке), называют дифференцируемой (в данной точке). Процесс вычисления производной называется дифференци́рованием. Обратный процесс — интегрирование.

Геометрический смысл производной состоит в том, что значение производной функции в точке x₀равно угловому коэффициенту касательной (тангенсу угла α ), проведенной к графику функции в точке с абсциссой x₀

где k – угловой коэффициент касательной, или

Пусть материальная точка движется по координатной прямой по закону x = x(t) , т.е. координата этой точки х – известная функция времени t.

Физический смысл производной состоит в том, что производная от координаты по времени естьмгновенная скорость:

Первая формула читается так: "Вэ от тэ равно пределу отношения изменения аргумента к изменению времени, при дэльта тэ стремящимся к нулю. (Здесь предел – от слова limit – лимит).

Алгебраический смысл- производная функции в точке есть угловой коэффициент касательной к графику этой функции в этой точке

39) Сложная функция. Правило ее дифференцирования.

(правило дифференцирования сложной функции) позволяет вычислить производную композиции двух и более функций на основе индивидуальных производных. Если функция f имеет производную в точке x₀, а функция g имеет производную в точке y₀ = f(x₀), то сложная функция h(x) = g(f(x)) также имеет производную в точке x₀.