
- •Свойства определителей
- •Системы линейных уравнений
- •Решение слау.
- •Действия над матрицами.
- •6) Линейные действия над векторами. Опр. Коллинеарности и компланарности векторов.
- •7) Исследование линейной зависимость векторов на плоскости и в пространстве.
- •8) Определение базиса векторов и координат вектора. Прямоугольная система координат.
- •9) Проекция вектора на ось. Координаты точки и вектора в прямоугольной системе.
- •10) Линейные действия над векторами в координатном представлении.
- •14) Вывод уравнения окружности
- •21) Полярная система координат.
- •22) Общее уравнение кривой второго порядка. Переход к каноническим уравнениям
- •24) Угол между плоскостями. Расстояние от точки до плоскости
- •25) Вывод канонического и общего уравнения прямой в пространстве. Переход между ними
- •26. . Элементы теории множеств
- •Символика математической логики
- •Определение функции в теории множеств
- •27. Общие свойства функций
- •28. Элементарные функции
- •29. Числовые последовательности
- •30. Бесконечно малые и бесконечно большие функции
- •36) Общие правила раскрытия неопределенностей
- •37) Опр. Средней скорости движения, мгновенной скорости, производной от функции. Алгебраический, физический, геометрический смысл производной.
- •40) Производные высших порядков. Дифференциалы высших порядков.
27. Общие свойства функций
Определение. Переменная у называется функцией переменной х, если каждому допустимому значению х соответствует определенное значение у.
Основные способы задания функций:
1.
Табличный способ:
 .
.
2. Аналитический способ: y = f(x), y = x2 (формула показывает, какие алгебраические действия надо совершить над х, чтобы получить соответствующее значение у).
3. Графический способ:
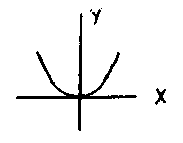
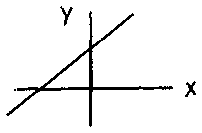
Определение. Функция имеет явную форму y = f(x), если зависимая переменная стоит слева в 1-ой степени и неявную форму, если х и у связаны более сложным образом.
Пример. у = х2, у2 + х2 = R2.
Обратная функция. Если идет процесс, связывающий несколько переменных, то выбор независимой переменной среди них может меняться.
Пример. Закон Ома имеет три равноправных формы: I = U/R, U = I R, R = U/I.
Определение. Обратная функция х = f–1(у) получается из прямой функции y = f(x), если в качестве аргумента взять у. Если y = f(x) устанавливает взаимно-однозначное соответствие между X = D(f) и Y = E(f), то х = f–1(у) выражает то же соответствие, причем Y = D(f–1), X = E(f–1).
Для перехода к обратной функции надо так преобразовать прямую функцию, чтобы аргумент х стоял слева в 1-ой степени.
Пример.
 .
.
Определение. Функция называется четной, если смена знака аргумента не меняет значения функции f(–x) = f(x) и нечетной, если смена знака аргумента меняет общий знак функции f(–x) = –f(x).
Пример. у = х2 и у = х3.
Любую функцию можно представить как сумму четной и нечетной функций. График четной функции симметричен относительно оси Оу, а нечетной – антисимметричен.
Определение. Функция называется периодической, если при изменении аргумента на постоянную величину значение функции не меняется f(x + T) = f(x). Наименьшее значение Т называется периодом.
Пример.
sin(x
+ 2 )
= sin(x).
Период Т
= 2
,
полный поворот радиус-вектора.
)
= sin(x).
Период Т
= 2
,
полный поворот радиус-вектора.
28. Элементарные функции
Среди множества функциональных зависимостей особое место занимают элементарные функции.
Основные элементарные функции:
1. Постоянная y = c, c = constR. |
|
2. Степенная y = xn, n R/{0}, D(f) зависит от n. |
|
3. Показательная у = ax, a > 0, a 1, D(f) = (–,+), E(f) = (0,– ). |
|
4. Логарифмическая y = logax, a > 0, a 1, D(f) = (0,+ ), E(f) = (–,+). |
|
5. Тригонометрические y = sinx, y = cosx, D(f) = (–,+) E(f) = [–1,+1]. |
|
y = tgx, D(f) = R\{ /2 + k },
k
=
|
|
y = ctgx, D(f) = R\{k }, k = 1, 2, . . . , E(f) = (–,+). |
|
6. Обратные тригонометрические y = arcsinx, D(f) = [–1, +1], главное значение y [– /2, /2]. |
|
y = arccosx, D(f) = [–1, +1], главное значение y [0, ]. |
|
y = arctgx, D(f) = (–, +), главное значение y (– /2, /2). |
|
y = arcctgx, D(f) = (–, +), главное значение y (0, ). |
|
Определение. Функция называется сложной, если в качестве её аргумента используется другая функция.
Выражение y = f [gf(x)] называется сложной функцией (суперпозицией), y = f(u) – внешней функцией, u = g(x) – внутренней функцией, u – называется сложным аргументом, х – независимым аргументом.
Пример. y = 3lg(1+ x2) или y = 3lg(u), где u = 1 + x2 – сложный аргумент.
Определение. Элементарными называются функции, записанные одной формулой и составленные из основных элементарных функций с помощью 4-х арифметических действий и операции суперпозиции.

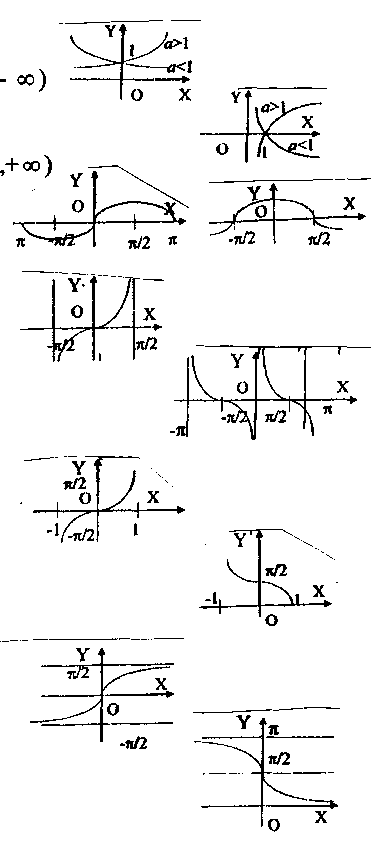

 1,
2,
. . . , E(f)
= (–,+).
1,
2,
. . . , E(f)
= (–,+).