26. . Элементы теории множеств

Под словом множество понимают совокупность некоторого числа однотипных элементов. Это базовое понятие. Множество обозначают заглавной буквой (А, B, C, . . .), а его элементы строчными буквами (a, b, c, . . .). Например, множество натуральных чисел N = {1, 2, 3, 4, . . . }.

При описании множеств используют специальные символы, которые означают:

 х Х – элемент х принадлежит множеству Х.

 х Х – элемент х не принадлежит множеству Х.

 A B – множество А является подмножеством B, т.е. состоит из части элементов множества В.

 Операция объединения А В. Объединение образуется из а А плюс b B.

 Операция пересечения А В. Пересечение образуется из элементов одновременно входящих и в А и в В.

 Операция разности А\В. Разность образуется из а А, не входящих в В.

 Операция дополнения В = В\А множества В до множества А, если В А.

 О – пустое множество (нет элементов).

 Если А = А_k и А_k А_i = 0, то А = А₁ + А₂ + . . . + А_n.

Пример. 1) {1, 2, 3} {2, 3, 4} = {1, 2, 3, 4},

2) {1, 2, 3} {2, 3, 4} = {2, 3},

3) {1, 2, 3}\{2, 3, 4} = {1},

4) {2, 3, 4} {1, 2, 3, 4} {1} = {2, 3, 4}.

Определение. Действия , , \ над подмножествами произвольного множества А составляют содержание алгебры множеств, которая называется булевой алгеброй.

Символика математической логики

Запись означает “не ”, т.е. отрицание.

– “из следует ” ( – символ импликации).

– “ эквивалентно ” ( – символ эквивалентности).

– “ и ” ( – символ конъюнкции).

– “ или ” ( – символ дизъюнкции).

– “для любого х А” ( – квантор всеобщности).

– “существует у В” ( – квантор существования).

– “для любого х из А имеет место ”.

– “существует единственный х из Х”.

Множество действительных чисел R состоит из рациональных и иррациональных чисел, изображается точками числовой оси Ох и обозначается R = (–оо, +оо). Подмножества R составляют интервалы (a, b) = {x: a < x < b}, промежутки [a, b] = {x: a x b} и их объединения [a, b), (a, b].

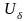Определение. -окрестностью (a) точки а R называется интервал (а – , а + ), где ( > 0), R. В проколотой -окрестности (a) исключается сама точка а – (a)\{a}.

Определение. Точка а А называется внутренней точкой множества А, если она обладает -окрестностью. Граничные точки промежутков не являются внутренними. Множество А называется открытым, если оно состоит из внутренних точек.

Определение функции в теории множеств

Определение. Между множествами Х и У установлено соответствие (Х > У), если для любого х Х указаны соответствующие ему у У.

Определение. Соответствие между Х и У называется взаимно-однозначным, если для любого х Х существует единственный элемент у У и наоборот.

Определение. Два множества Х и У называются эквивалентными (Х У), если между ними можно установить взаимно-однозначное соответствие.

Определение. Функцией y = f(x), определенной на множестве Х и принимающей значения на множестве Y, называется правило соответствия между этими множествами, при котором для каждого х Х существует единственный элемент у У.

Символическая запись: .

Множество X = D(f) – область определения функции; Y = E(f) – область значений функции; x – независимая переменная (аргумент), y – зависимая переменная (функция).

Важнейшие свойства материи – движение и причинно-следственная связь. Однако математический аппарат для описания этих свойств появился только в 17 веке, после рождения фундаментальных понятий – переменная величина и функция. Вся математика до 17 века называется математикой постоянной величины, а после 17 века – новая математика, она хорошо приспособлена для описания реальных процессов.