21) Полярная система координат.

     Для описания положения точки  P  на плоскости можно использовать полярные координаты  r  и  φ, где  r – расстояние от точки  P  до начала координат, называемого полюсом;  φ – угол, образованный лучом 0 P с положительным направлением полярной оси. При этом величина угла считается положительной, если отсчет ведется против часовой стрелки, а отрицатательная величина угла соответствует отсчету по часовой стрелке. Для числа  z = 0  полярный угол не определен. 

  Рассмотрим комплексную плоскость x0y. В качестве полярной оси выберем ось 0x; при этом начало прямоугольной системы координат играет роль полюса полярной системы координат.

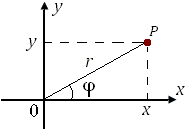  Рис. 1. Декартовы и полярные координаты точки плоскости.

      Тогда полярные координаты   связаны с декартовыми прямоугольными координатами (x,y) следующими соотношениями:

		(1)
		(2)
	,	(3)
	,	(4)
		(5)
	или        .	(6)

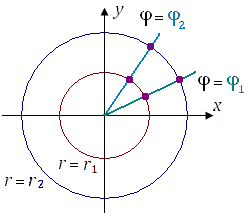
      Координатными линиями в полярной системе координат являются концентрические окружности   и лучи  . Пересечение двух таких линий определяет единственную точку плоскости.

22) Общее уравнение кривой второго порядка. Переход к каноническим уравнениям

Кривая второго порядка — геометрическое место точек, декартовы прямоугольные координаты которых удовлетворяют уравнению вида

в котором по крайней мере один из коэффициентов   отличен от нуля

Ax² + 2Bxy + Cy² + Dx + Ey + F = 0

Переход к каноническим уравнениям.

??????????????????????????????????????????????

23) Вывод трех форм уравнения плоскости в пространстве

• Уравнение плоскости в отрезках:

где  ,  ,   — отрезки, отсекаемые плоскостью на осях   и  .

• Уравнение плоскости, проходящей через точку   перпендикулярно вектору нормали  :

в векторной форме:

• Уравнение плоскости, проходящей через три заданные точки 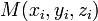 , не лежащие на одной прямой:

(смешанное произведение векторов), иначе

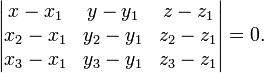
24) Угол между плоскостями. Расстояние от точки до плоскости

   Угол между плоскостями 

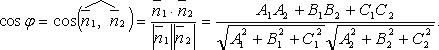
Расстояние от точки до плоскости --- это наименьшее из расстояний между этой точкой и точками плоскости. Известно, что расстояние от точки до плоскости равно длине перпендикуляра, опущенного из этой точки на плоскость. Если плоскость задана уравнением  , то расстояние   от точки   до этой плоскости можно вычислить по формуле

25) Вывод канонического и общего уравнения прямой в пространстве. Переход между ними

Переход от общих уравнений прямой к каноническим (параметрическим) требует несколько больших усилий.

Пусть прямая задана общими уравнениями:

(5)

Чтобы записать канонические (параметрические) уравнения этой прямой, необходимо найти ее направляющий вектор и координаты какой-нибудь точки на прямой. Координаты точки 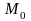найти легко – это одно из решений системы уравнений (5). Выясним, как можно найти направляющий вектор .

Пусть и – плоскости, уравнения которых входят в общие уравнения прямой, и – нормальные векторы к плоскостям и соответственно.

Так как прямая лежит в плоскости , то векторы и перпендикулярны.

Т ак как прямая лежит в плоскости , то векторы и тоже перпендикулярны.

Следовательно, в качестве можем взять векторное произведение векторов и (см. определение векторного произведения в §9).