28. Правило Лопиталя

Пусть функции f(x) и g(x) дифференцируемы в некоторой окрестности точки a, за исключением, быть может, самой точки a, и пусть   или  . Тогда, если существует предел отношения производных этих функций  , то существует и предел отношения самих функций f(x)/g(x) при x→а, причем

(1)

Таким образом, коротко правило Лопиталя можно сформулировать следующим образом: предел отношения двух бесконечно малых или двух бесконечно больших величин равен пределу отношения их производных.

Замечание. Отметим, что формула (1) справедлива только в том случае, если предел, стоящий справа, существует. Может случиться, что предел, стоящий слева существует, в то время как предел, стоящий в правой части равенства, не существует.

Например, найти  . Этот предел существует  . Но отношение производных (1+cosx)/1=1+cos x при x→∞ не стремится ни к какому пределу.

Заметим, что если отношение производных опять представляет собой неопределенность вида 0/0 или ∞/∞, то можно снова применить сформулированную теорему, то есть перейти к отношению вторых производных и так далее.

Вспомним, что к этим двум случаям сводятся случаи других неопределенностей: ∞·∞; 0·∞.

Для раскрытия неопределенностей 1∞, 10, ∞0 нужно прологарифмировать данную функцию и найти предел ее логарифма.

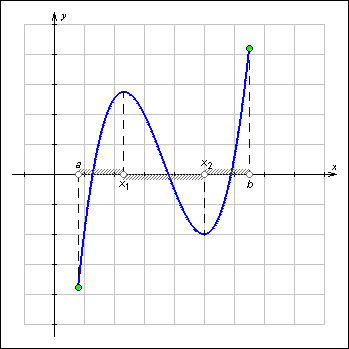
29. Интервалы монотонности функции

Функция f (x) называется возрастающей на промежутке D, если для любых чисел x₁ и x₂ из промежутка D таких, что x₁ < x₂, выполняется неравенствоf (x₁) < f (x₂).

Функция f (x) называется убывающей на промежутке D, если для любых чисел x₁ и x₂ из промежутка D таких, что x₁ < x₂, выполняется неравенство f (x₁) > f (x₂).

Рисунок 1.3.5.1. Промежутки возрастания и убывания функции

На показанном на рисунке графике функция y = f (x),   возрастает на каждом из промежутков [a; x₁) и(x₂; b] и убывает на промежутке (x₁; x₂). Обратите внимание, что функция возрастает на каждом из промежутков [a; x₁) и (x₂; b], но не на объединении промежутков 

Если функция возрастает или убывает на некотором промежутке, то она называется монотонной на этом промежутке.

Заметим, что если f – монотонная функция на промежутке D (f (x)), то уравнение f (x) = const не может иметь более одного корня на этом промежутке.

Действительно, если x₁ < x₂ – корни этого уравнения на промежутке D (f(x)), то f (x₁) = f (x₂) = 0, что противоречит условию монотонности.

30. Экстремумы функции

Точки максимума и минимума называются точками экстремума, а значения функции в этих точках - ее экстремумами.

Необходимые условия экстремума. Если точка x_о является точкой экстремума функции f(x), то либо f (x_о) = 0, либо f (x_о) не существует. Такие точки называют критическими,причем сама функция в критической точке определена. Экстремумы функции следует искать среди ее критических точек.

Первое достаточное условие. Пусть x_о - критическая точка. Если f  (x) при переходе через точку x_о меняет знак плюс на минус, то в точке x_о функция имеет максимум, в противном случае - минимум. Если при переходе через критическую точку производная не меняет знак, то в точке x_о экстремума нет.

Второе достаточное условие. Пусть функция f(x) имеет производную  f  (x) в окрестности точки x_о и вторую производную  в самой точке x_о. Если f (x_о) = 0, >0 (<0), то точка x_о является точкой локального минимума (максимума) функции f(x). Если же =0, то нужно либо пользоваться первым достаточным условием, либо привлекать высшие производные.

На отрезке [a,b] функция y = f(x) может достигать наименьшего или наибольшего значения либо в критических точках, либо на концах отрезка [a,b].

31. Второй достаточный признак экстремума.

Пусть функция f(x) имеет производную f  (x) в окрестности точки x_о и вторую производную  в самой точке x_о. Если f (x_о) = 0, >0 (<0), то точка x_о является точкой локального минимума (максимума) функции f(x). Если же =0, то нужно либо пользоваться первым достаточным условием, либо привлекать высшие производные.

32. Наибольшее и наименьшее значение функции в интервале

Наибольшим значением функции y = f(x) на промежутке X называют такое значение , что для любого справедливо неравенство .

Наименьшим значением функции y = f(x) на промежутке X называют такое значение , что для любого справедливо неравенство .

33.Интервалы выпуклости и вогнутости

График функции y=f(x) называется выпуклым на интервале (a; b), если он расположен ниже любой своей касательной на этом интервале.

График функции y=f(x) называется вогнутым на интервале (a; b), если он расположен выше любой своей касательной на этом интервале.

34.Точки перегиба

Точка графика непрерывной функции, отделяющая его выпуклую часть от вогнутой, называется точкой перегиба.

Очевидно, что в точке перегиба касательная, если она существует, пересекает кривую, т.к. с одной стороны от этой точки кривая лежит под касательной, а с другой стороны – над нею.

Определим достаточные условия того, что данная точка кривой является точкой перегиба.

Теорема. Пусть кривая определяется уравнением y = f(x). Если f ''(x0) = 0 или f ''(x0) не существует и при переходе через значениеx = x0 производная f ''(x) меняет знак, то точка графика функции с абсциссой x = x0 есть точка перегиба.

Доказательство. Пусть f ''(x) < 0 при x < x0 и f ''(x) > 0 при x > x0. Тогда при x < x0 кривая выпукла, а при x > x0 – вогнута. Следовательно, точка A, лежащая на кривой, с абсциссой x0 есть точка перегиба. Аналогично можно рассматривать второй случай, когда f ''(x) > 0 при x < x0 и f ''(x) < 0 при x > x0.

Таким образом, точки перегиба следует искать только среди таких точек, где вторая производная обращается в нуль или не существует.