14. Сравнение бесконечно малых величин

Определения. Пусть при   функции f(x) и g(x) являются бесконечно малыми. Тогда:

1. Если   , то f(x) называется бесконечно малой высшего порядка относительно g(x).

2. Если   (конечен и отличен от 0), то f(x) называется бесконечно малой n-го порядка относительно g(x).

3. Если   , то f(x) и g(x) называются эквивалентными бесконечно малыми.Эквивалентность записывается так:   .

Свойства эквивалентных бесконечно малых:

1. Разность двух эквивалентных бесконечно малых есть бесконечно малая высшего порядка относительно каждой из них.

2. Если из суммы нескольких бесконечно малых разных порядков отбросить бесконечно малые высших порядков, то оставшаяся часть, называемая главной, эквивалентна всей сумме.

15. Сравнение бесконечно больших величин

1)  , т.е. предел отношения функций существует и равен бесконечности. В этом случае говорят, что p(x) бесконечно большая функция более высокого порядка.

2)  , т.е. предел отношения функций существует и равен С - некоторой константе. В этом случае говорят, что p(x) и q(x) бесконечно большие функции одного порядка.

3)  , т.е. предел отношения функций существует и равен нулю. В этом случае говорят, что q(x) бесконечно большая функция более высокого порядка.

4) Если данный предел:   не существует, в этом случае мы ничего не можем сказать о сравниваемых функциях и поэтому говорят, что функции не сравнимы.

16. Производная и ее геометрический смысл.

Производная - это предел отношения приращения функции к приращению ее аргумента при стремлении приращения аргумента к нулю, если таковой предел существует.

Рассмотрим график функции y = f ( x ):

Из рис.1 видно, что для любых двух точек A и B графика функции:  xf(x0+ x)−f(x0)=tg , где   - угол наклона секущей AB. Таким образом, разностное отношение равно угловому коэффициенту секущей. 

производная функции в точке есть угловой коэффициент касательной к графику этой функции в этой точке.

17.Уравнение касательной и нормали к линии.

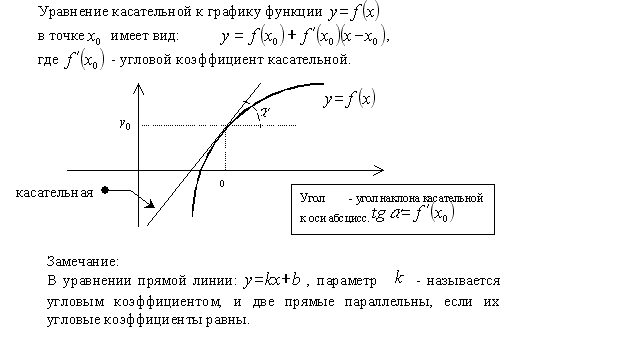
уравнение нормали

18. Правила дифференцирования

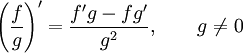При дифференцировании константу можно выносить за производную:    Правило дифференцирования суммы функций:    Правило дифференцирования разности функций:    Правило дифференцирования произведения функций (правило Лейбница):    Правило дифференцирования частного функций:    Правило дифференцирования функции в степени другой функции:   

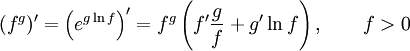
19.Производные сложной и обратной функции

Производная сложной функции

Рассмотрим сложную функцию y = y(u(x))

Теорема 4. Если функции y = y(u), u = u(x) дифференцируемы (т.е. существуют производные y'_u, u'_x), тогда сложная функция y = y(u(x)) дифференцируема и y'_x = y'_u u'_x.

Доказательство

Если аргумент x получит приращение Δx, то функция u получит приращение Δu = u(x + Δx) − u(x), а функция y получит приращение Δy = y(u + Δu) − y(u). Но тогда, воспользовавшись свойствами предела функции, получаем

Теорема доказана.

Производная обратной функции

Рассмотрим функцию y = f(x), для которой существует обратная функция x = g(y).

Теорема 5. Если обратная функция x = g(y) дифференцируема и g'(y) ≠ 0, то функцияy=f(x) дифференцируема, и 

Доказательство

Если аргумент x получит приращение Δx, то функция f получит приращение Δy = f(x + Δx) − f(x). С другой стороны, для обратной функции g приращения Δx, Δy связаны следующим образом:Δx=g(y + Δy) − g(y).

Тогда получаем

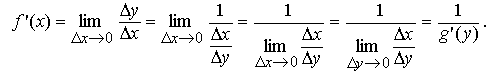
Теорема доказана.