
- •Раздел 1 Основные термины и определения теории надёжности
- •1.1 Объект, система и элементы
- •1.2 Состояния и события
- •Постепенные – это отказы, которые наступают в результате длительного, постепенного изменения одного или нескольких параметров объекта.
- •1.3 Наработка и ресурс
- •1.4 Надежность
- •Раздел 2 Показатели надежности невосстанавливаемых объектов
- •2.1 Функции распределения и надёжности наработки до отказа
- •2.2 Плотность распределения наработки до отказа
- •2.3 Вероятности отказа и безотказной работы
- •2.4 Интенсивность отказов
- •2.5 Средняя наработка до отказа
- •Раздел 3 Законы распределения наработки до отказа
- •3.1 Экспоненциальное распределение
- •3.2 Нормальное распределение (распределение Гаусса)
- •3.3 Усечённое нормальное распределение
- •3.4 Логарифмически нормальное (логнормальное) распределение
- •3.5 Распределение Рэлея
- •3.6 Распределение Вейбулла
- •3.7 Гамма-распределение
- •3.8 Смесь распределений
- •Раздел 4 Потоки отказов и показатели надежности восстанавливаемых объектов
- •4.1 Понятие потока отказов. Простейший (пуассоновский) поток
- •4.2 Показатели безотказности
- •4.3 Показатели ремонтопригодности
- •4.4 Показатели долговечности
- •4.5 Комплексные показатели надежности
- •Раздел 5 Расчёт надёжности систем без учёта восстановления Расчёт надёжности системы – это определение её показателей надёжности по известным показателям надёжности элементов.
- •5.1 Основные этапы расчёта надежности
- •5.2 Способы соединения элементов и составление структурной схемы системы
- •5.3 Методы расчета надёжности невосстанавливаемых систем
- •5.3.1 Расчет надежности систем с последовательным и параллельным соединением элементов
- •5.3.2 Расчёт надёжности систем со сложной структурой
- •6.4 Резервирование систем
- •Раздел 6 Расчёт надёжности систем с учётом восстановления
- •6.1 Граф состояний системы
- •6.2 Расчет надежности восстанавливаемой системы с помощью уравнений типа массового обслуживания
- •6.3 Матрица состояний
- •6.3 Расчет надежности восстанавливаемой системы с помощью интегральных уравнений
- •Раздел 7 Оценка надёжности объектов по результатам испытаний
- •7.1 Виды испытаний на надежность
- •7.2 Определительные испытания
- •8.3 Контрольные испытания
- •Раздел 9 Обеспечение надёжности систем при эксплуатации
- •9.1 Организация эксплуатации
- •9.2 Классификация запасных частей
- •9.3 Организация пополнения запаса
- •9.4 Расчет числа невосстанавливаемых запасных частей с периодическим пополнением по вероятности достаточности
- •9.5 Расчет количества восстанавливаемых запасных частей по вероятности достаточности
- •9.6 Техническое обслуживание
- •Раздел 10 Диагностика автоматизированных систем
- •10.1 Классификация видов диагностирования
- •10.2 Классификация методов диагностирования
- •10.3 Показатели диагностирования
- •10.4 Математические модели объектов диагностирования
- •10.5 Системы технического диагностирования
- •10.6 Таблица функций неисправностей (тфн)
- •10.7 Алгоритмы диагностирования
- •Раздел 11 Анализ надежности программного обеспечения
- •11.1 Основные понятия надежности программного обеспечения
3.6 Распределение Вейбулла
Функция распределения наработки до отказа
![]() ,
,
где
![]() – параметр формы распределения;
– параметр формы распределения;
![]() –
параметр масштаба распределения.
–
параметр масштаба распределения.
Плотность распределения наработки до отказа
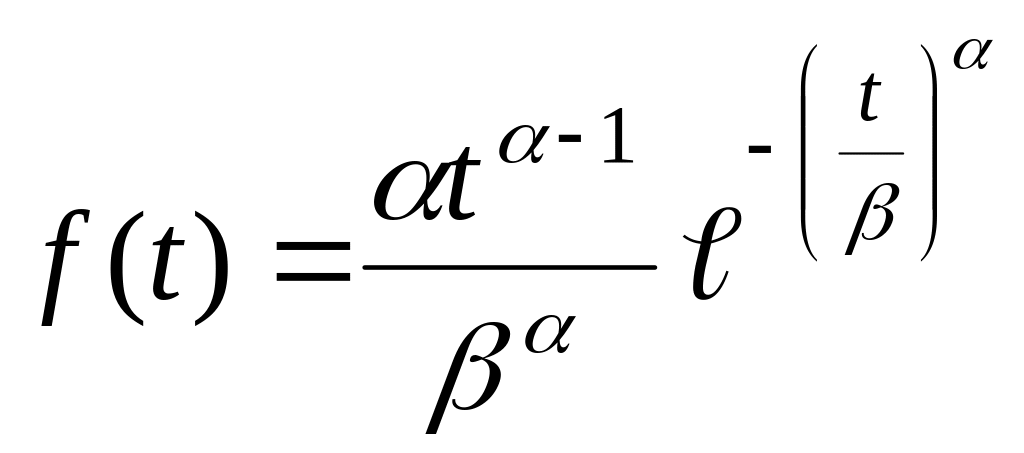 .
.
При
![]() распределение
Вейбулла совпадает с экспоненциальным
распределение
Вейбулла совпадает с экспоненциальным
(рис. 3.1), когда интенсивность отказов постоянна.
При
![]() превращается в распределение Рэлея
(рис. 3.6).
превращается в распределение Рэлея
(рис. 3.6).
При
![]() интенсивность отказов монотонно
возрастает (рис. 3.7).
интенсивность отказов монотонно
возрастает (рис. 3.7).
При
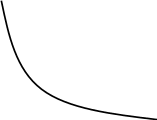
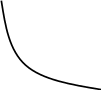
![]() монотонно убывает (рис. 3.8).
монотонно убывает (рис. 3.8).
![]()
1

Время, t
0
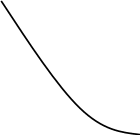
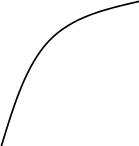
Рис.
3.7 График изменения показателей
надёжности для
распределение
Вейбулла, при
1
Время, t
0
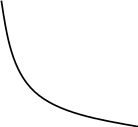
Рис.
3.8
График
изменения показателей надёжности для
распределение
Вейбулла, при
Средняя наработка до отказа
![]() ,
,
где
![]() – гамма-функция.
– гамма-функция.
Среднее квадратическое отклонение
![]() .
.
Распределение Вейбулла является достаточно универсальным, так как позволяет, варьируя его параметрами, добиваться различной формы кривой интенсивности отказов.
3.7 Гамма-распределение
Функция распределения наработки до отказа
![]() ,
,
где
– параметр формы распределения;
–
параметр масштаба распределения;
![]() – гамма-функция Эйлера.
– гамма-функция Эйлера.
Плотность распределения
![]() .
.
Средняя наработка до отказа
![]() .
.
Среднее квадратическое отклонение
![]() .
.
Графики показателей надёжности при гамма-распределении представлены на рис. 3.9.
1


0
Время, t
Рис.
3.9 График показателей надёжности для
гамма-распределения
При интенсивность отказов возрастает, при убывает, а при становится постоянной, т.е. гамма-распределение превращается в экспоненциальное.
Гамма-распределение наиболее хорошо описывает распределение суммы независимых случайных величин, каждая из которых распределена по экспоненциальному закону.
При
целом
гамма-распределение называется
распределением
Эрланга порядка
.
Сумма
случайных величин, имеющих экспоненциальное
распределение с параметром
,
имеет распределение Эрланга с параметрами
и
![]() .
Функция распределения при этом будет
иметь вид
.
Функция распределения при этом будет
иметь вид
![]() .
.
3.8 Смесь распределений
Смесь распределений определяется, как линейная комбинация нескольких распределений. При этом выражения для основных показателей надежности будут иметь вид
![]() ,
,
![]() ,
,
![]() ,
,
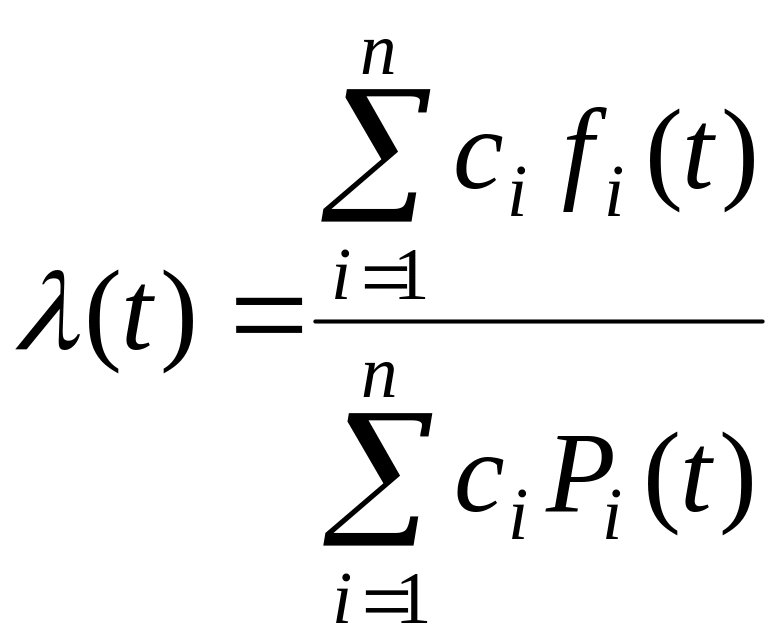 ,
,
где
![]() – коэффициент веса i-го
показателя;
– коэффициент веса i-го
показателя;
![]() .
.
Выбор того или иного закона распределения наработки до отказа определённого типа объектов должен основываться на анализе изменений их параметров на протяжении всего периода эксплуатации.
Раздел 4 Потоки отказов и показатели надежности восстанавливаемых объектов
4.1 Понятие потока отказов. Простейший (пуассоновский) поток
Поток отказов это последовательность отказов, происходящих один за другим в случайные моменты времени.
Существует множество математических описаний потоков отказов. Наиболее распространённым из них является простейший (пуассоновский) поток отказов.
Простейший (пуассоновский) поток – это поток отказов, который одновременно обладает свойствами стационарности, ординарности и отсутствия последействия.
Свойство
стационарности. Поток
называют стационарным,
если числа отказов
![]() ,
,
![]() ,
…,
,
…,
![]() соответственно на отрезках времени
соответственно на отрезках времени
![]() ,
,
![]() ,
…,
,
…,
![]() зависят
только от длительности этих отрезков
зависят
только от длительности этих отрезков
![]() ,
,
![]() ,
…,
,
…,
![]() и
не зависит от выбора общего момента
начала
отрезков. В противном случае поток
называют нестационарным.
Выполнение
требования стационарности означает,
что вероятностные характеристики потока
не зависят от времени. В частности,
закон распределения числа отказов на
любом промежутке времени
и
не зависит от выбора общего момента
начала
отрезков. В противном случае поток
называют нестационарным.
Выполнение
требования стационарности означает,
что вероятностные характеристики потока
не зависят от времени. В частности,
закон распределения числа отказов на
любом промежутке времени
![]() не зависит от самих значений
и
не зависит от самих значений
и
![]() ,
а зависит только от их разности
,
а зависит только от их разности
![]() .
.
Пример. Изменение во времени условий эксплуатации: температуры, вибрации, запылённости, квалификации обслуживающего персонала и других приводит к нестационарности.
Свойство
отсутствия последствий. Поток
отказов называют потоком
без последействия,
если
для любого набора непересекающихся
промежутков времени
,
,
…,
числа отказов на этих промежутках
![]() ,
,
![]() ,
…,
,
…,
![]() представляют собой взаимно независимые
случайные величины. В частности,
выполнение требования отсутствия
последействия означает, что распределение
числа отказов на любом промежутке
времени не зависит от течения потока
до и после этого промежутка времени.
представляют собой взаимно независимые
случайные величины. В частности,
выполнение требования отсутствия
последействия означает, что распределение
числа отказов на любом промежутке
времени не зависит от течения потока
до и после этого промежутка времени.
Пример. Последействия могут иметь место и из-за недостаточного качества восстановления, когда свойства объекта не полностью регенерируются после отказа, а также в ситуации, когда отказ одного элемента вызывает ухудшение условий работы иных элементов.
Свойство ординарности. Поток называют ординарным, если
![]()
где
![]()
вероятность
возникновения по меньшей мере двух
отказов в течение промежутка времени
длиной
вероятность
возникновения по меньшей мере двух
отказов в течение промежутка времени
длиной
![]() .
.
Ординарность означает практическую невозможность возникновения двух или более отказов одновременно.
Пример. Неординарность возникает в системе при условиях эксплуатации сверх допустимых пределов.
Вероятность
возникновения
![]() отказов
(
=0,
1, 2 …) на отрезке времени длиной
определяется
распределением Пуассона
отказов
(
=0,
1, 2 …) на отрезке времени длиной
определяется
распределением Пуассона
![]() (4.1)
(4.1)
где
![]() параметр
распределения.
параметр
распределения.
