
- •Раздел 1 Основные термины и определения теории надёжности
- •1.1 Объект, система и элементы
- •1.2 Состояния и события
- •Постепенные – это отказы, которые наступают в результате длительного, постепенного изменения одного или нескольких параметров объекта.
- •1.3 Наработка и ресурс
- •1.4 Надежность
- •Раздел 2 Показатели надежности невосстанавливаемых объектов
- •2.1 Функции распределения и надёжности наработки до отказа
- •2.2 Плотность распределения наработки до отказа
- •2.3 Вероятности отказа и безотказной работы
- •2.4 Интенсивность отказов
- •2.5 Средняя наработка до отказа
- •Раздел 3 Законы распределения наработки до отказа
- •3.1 Экспоненциальное распределение
- •3.2 Нормальное распределение (распределение Гаусса)
- •3.3 Усечённое нормальное распределение
- •3.4 Логарифмически нормальное (логнормальное) распределение
- •3.5 Распределение Рэлея
- •3.6 Распределение Вейбулла
- •3.7 Гамма-распределение
- •3.8 Смесь распределений
- •Раздел 4 Потоки отказов и показатели надежности восстанавливаемых объектов
- •4.1 Понятие потока отказов. Простейший (пуассоновский) поток
- •4.2 Показатели безотказности
- •4.3 Показатели ремонтопригодности
- •4.4 Показатели долговечности
- •4.5 Комплексные показатели надежности
- •Раздел 5 Расчёт надёжности систем без учёта восстановления Расчёт надёжности системы – это определение её показателей надёжности по известным показателям надёжности элементов.
- •5.1 Основные этапы расчёта надежности
- •5.2 Способы соединения элементов и составление структурной схемы системы
- •5.3 Методы расчета надёжности невосстанавливаемых систем
- •5.3.1 Расчет надежности систем с последовательным и параллельным соединением элементов
- •5.3.2 Расчёт надёжности систем со сложной структурой
- •6.4 Резервирование систем
- •Раздел 6 Расчёт надёжности систем с учётом восстановления
- •6.1 Граф состояний системы
- •6.2 Расчет надежности восстанавливаемой системы с помощью уравнений типа массового обслуживания
- •6.3 Матрица состояний
- •6.3 Расчет надежности восстанавливаемой системы с помощью интегральных уравнений
- •Раздел 7 Оценка надёжности объектов по результатам испытаний
- •7.1 Виды испытаний на надежность
- •7.2 Определительные испытания
- •8.3 Контрольные испытания
- •Раздел 9 Обеспечение надёжности систем при эксплуатации
- •9.1 Организация эксплуатации
- •9.2 Классификация запасных частей
- •9.3 Организация пополнения запаса
- •9.4 Расчет числа невосстанавливаемых запасных частей с периодическим пополнением по вероятности достаточности
- •9.5 Расчет количества восстанавливаемых запасных частей по вероятности достаточности
- •9.6 Техническое обслуживание
- •Раздел 10 Диагностика автоматизированных систем
- •10.1 Классификация видов диагностирования
- •10.2 Классификация методов диагностирования
- •10.3 Показатели диагностирования
- •10.4 Математические модели объектов диагностирования
- •10.5 Системы технического диагностирования
- •10.6 Таблица функций неисправностей (тфн)
- •10.7 Алгоритмы диагностирования
- •Раздел 11 Анализ надежности программного обеспечения
- •11.1 Основные понятия надежности программного обеспечения
Раздел 2 Показатели надежности невосстанавливаемых объектов
Показателями надежности – это количественные характеристики одного или нескольких свойств, составляющих надежность объекта.
Показатели надежности представляются в двух формах
вероятностная;
cтатистическая.
Вероятностная форма представляет собой некую аналитическую зависимость, в то время как статистическая форма получается по результатам испытаний на надежность и строится для некоторой совокупности объектов.
Основными показателями надёжности невосстанавливаемых объектов являются показатели безотказности.
2.1 Функции распределения и надёжности наработки до отказа
Наработка
до отказа
![]() ,
как
и любая иная случайная величина,
описывается функцией распределения
,
как
и любая иная случайная величина,
описывается функцией распределения
![]() .
Эта функция определяется как вероятность
.
Эта функция определяется как вероятность
![]() случайного события, которое заключатся
в том, что наработка до отказа
случайного события, которое заключатся
в том, что наработка до отказа
![]() меньше некоторой заданной наработки
меньше некоторой заданной наработки
![]()
![]() .
(2.1)
.
(2.1)
Эта
вероятность рассматривается как функция
![]() во
всем диапазоне возможных значений
величины
.
Функция
распределения любой случайной величины
является неубывающей функцией времени
.
во
всем диапазоне возможных значений
величины
.
Функция
распределения любой случайной величины
является неубывающей функцией времени
.
Примерный вид функции дан на рис. 2.1.
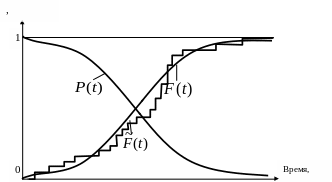
Рис.
2.1 Примерный вид функции распределения
и
функции надежности
![]()
Так
как значения
не
могут быть отрицательны, то![]() .
При
.
При
![]() величина
стремится
к единице.
величина
стремится
к единице.
Кроме вероятностного определения функции , для нее можно привести и статистические определения, которые используются при испытаниях на надежность.
Обозначения статистических определений далее будут отмечаться волнистой чертой сверху.
Для рассмотрения статистических определений показателей надежности невосстанавливаемых объектов предположим:
на испытания поставлено
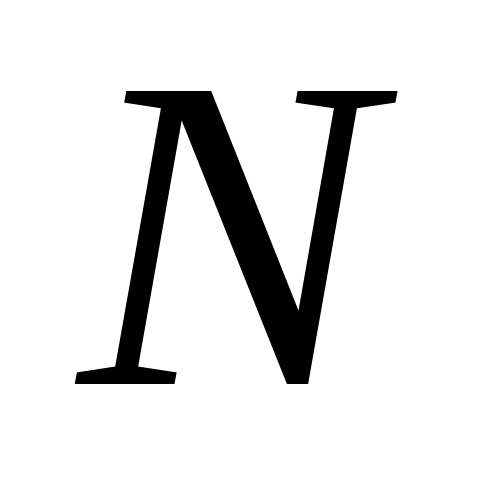 одинаковых объектов;
одинаковых объектов;
условия испытаний одинаковы;
испытания каждого из объектов проводятся до его отказа.
Обозначим
![]() число
объектов, отказавших к моменту
,
т. е. на интервале
число
объектов, отказавших к моменту
,
т. е. на интервале
![]() .
Очевидно,
что
.
Очевидно,
что
![]() ,
а при
величина
,
а при
величина
![]() .
.
Статистическим определением функции распределения является функция
![]() ,
(2.2)
,
(2.2)
причем
при
![]() величина
величина
![]() ,
а
при
,
а
при
![]() .
.
График
функции распределения
![]() представляет
собой ступенчатую линию со скачками,
кратными
представляет
собой ступенчатую линию со скачками,
кратными
![]() в
моменты
отказов (рис. 2.1). С ростом числа
испытываемых
объектов функция распределения
сходится
по вероятности к распределению
.
в
моменты
отказов (рис. 2.1). С ростом числа
испытываемых
объектов функция распределения
сходится
по вероятности к распределению
.
Так как события, которые заключаются в наступлении или не наступлении отказа к моменту , являются противоположными, то в соответствии с (2.1) введем еще одну функцию
![]() ,
(2.3)
,
(2.3)
которую
часто называют функцией
надежности.
Так как при
объект работоспособен, то
![]() .
С увеличением времени
монотонно
убывает, а при
величина
.
С увеличением времени
монотонно
убывает, а при
величина
![]() .
Примерный
вид функции
показан на
рис. 2.1.
.
Примерный
вид функции
показан на
рис. 2.1.
Статистическое определение функции надежности следует из (2.2)
![]() ,
(2.4)
,
(2.4)
где
![]() - число
объектов, работоспособных к моменту
времени
.
- число
объектов, работоспособных к моменту
времени
.
