8.3 Контрольные испытания

При проведении контрольных испытаний объектов, обязательными являются испытания на безотказность. Испытания на ремонтопригодность, сохраняемость и долговечность проводят в тех случаях, когда это предусмотрено стандартами, техническими заданиями или техническими условиями на конкретный объект.

Для проведения контрольных испытаний из совокупности (партии) однородных объектов составляется некоторая выборка и проводятся испытания на надежность попавших в эту выборку объектов. По результатам испытания выборки делается заключение о соответствии всей партии предъявляемым требованиям.

Предположение о соответствии партии требованиям к надёжности называют нулевой гипотезой.

По результатам испытаний имеет место одна из следующих четырех ситуаций:

1. Партия удовлетворяет требованиям; по результатам испытаний подтвердилось нулевая гипотеза и принято решение о принятии партии. Это решение правильно.

2. Партия удовлетворяет требованиям, но по результатам испытаний нулевая гипотеза не подтвердилась. Это произошло потому, что случайно составленная выборка содержала повышенное число отказавших объектов по сравнению с совокупностью. Принята альтернативная гипотеза; это решение неправильно и невыгодно для изготовителя приборов. При этом произошла ошибка, вероятность которой называют риском поставщика (изготовителя) .

3. Партия не удовлетворяет требованиям, по результатам испытаний нулевая гипотеза не подтвердилась. Принята альтернативная гипотеза, т. е. решение о непринятии партии. Это решение правильно.

4. Партия не удовлетворяет требованиям, но по результатам испытаний подтвердилась нулевая гипотеза о соответствии требованиям к надежности, так как выборка содержала повышенное число неотказавших объектов по сравнению со всей партией. Принято неправильное решение, но оно невыгодно в отличие от п. 2 не изготовителю, а потребителю – заказчику этих объектов. Произошла ошибка, вероятность которой называют риском потребителя (заказчика) .

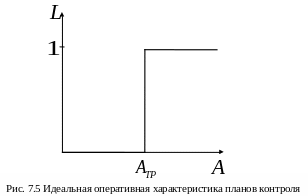
Зависимость вероятности L приемки партии от показателя надежности A (называемая оперативной характеристикой плана контроля) показана на рис. 7.5. Пусть требуемое значение показателя надежности. В этой ситуации нулевая гипотеза . Если она справедлива, то партия принимается с вероятностью, равной единице, причем . Альтернативная гипо­теза заключается в том, что . При этом партия бракуется с вероятностью, равной единице, причем . Однако такая идеальная оперативная характеристика недостижима, так как требует бесконечного объема наблюдений.

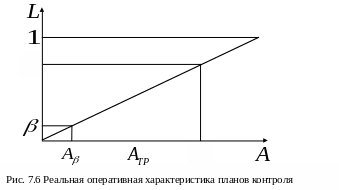
В реальной ситуации вводятся два уровня контролируемого показателя надежности: приемочный и браковочный (рис. 7.6). Если , то приборы должны приниматься с достаточно высокой вероятностью, не ниже , если , то приборы должны браковаться с достаточно высокой вероятностью, не ниже . При этом риск поставщика , риск потребителя . Тем самым проверку нулевой гипотезы при альтернативе заменяем другой задачей – проверкой нулевой гипотезы при альтернативе . Чем ближе к , тем больший объем испытаний необходим для принятия достоверного решения о соответствии партии.

Контрольные испытания на безотказность проводятся, как правило, одно или двухступенчатым методом. При проведении испытаний одноступенчатым методом образцы, вошедшие в выборку объема d, испытывают в течение времени . По окончании испытаний определяют число наступивших отказов n. Если оно равно или меньше приемочного числа отказов c, определенного в зависимости от величин , , и , то нулевая гипотеза подтверждается и партию принимают. Если же , то подтверждается альтернативная гипотеза и партию не принимают.