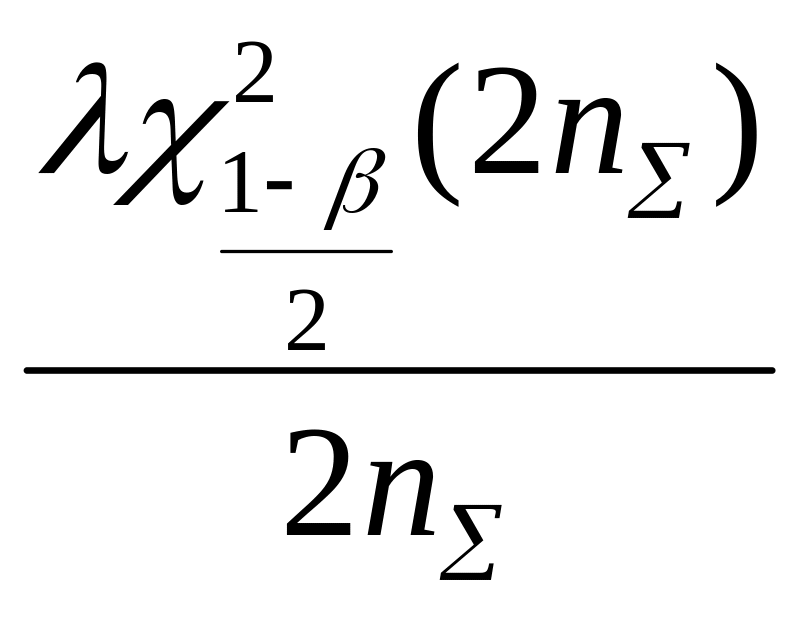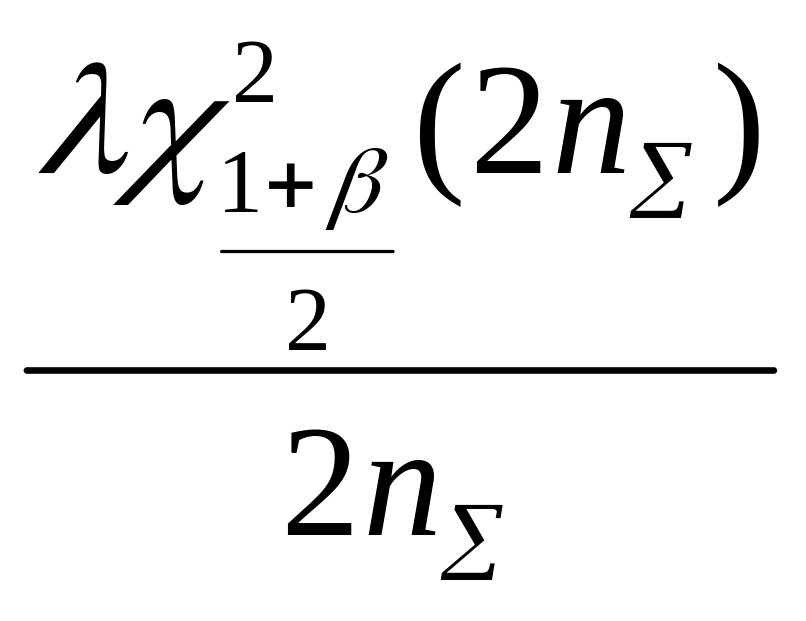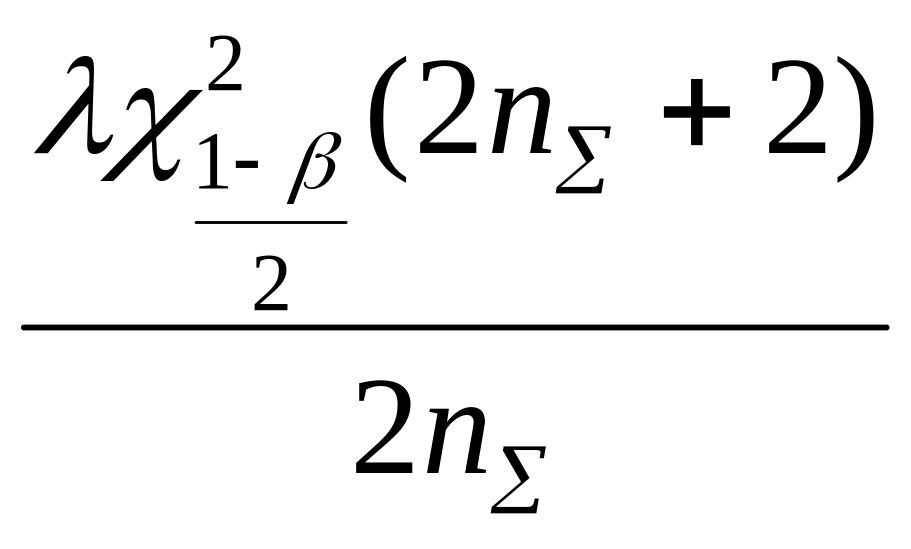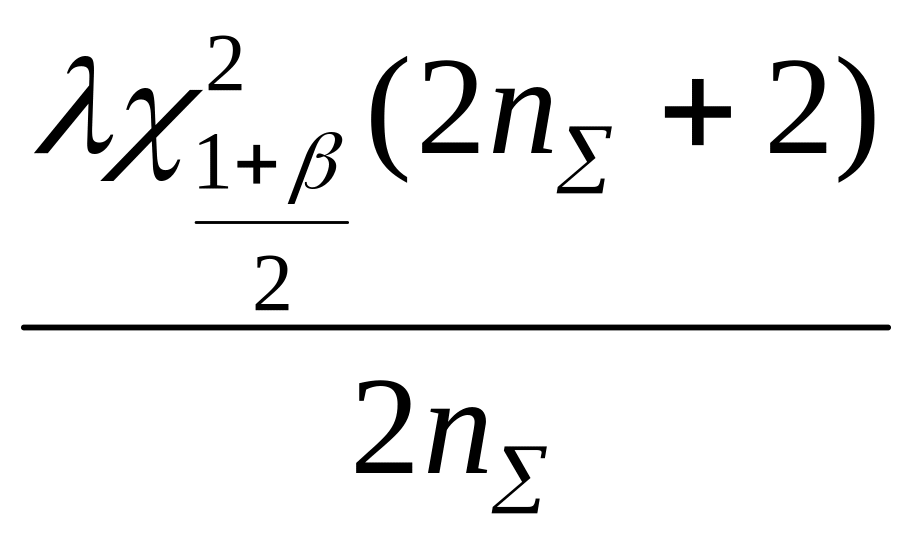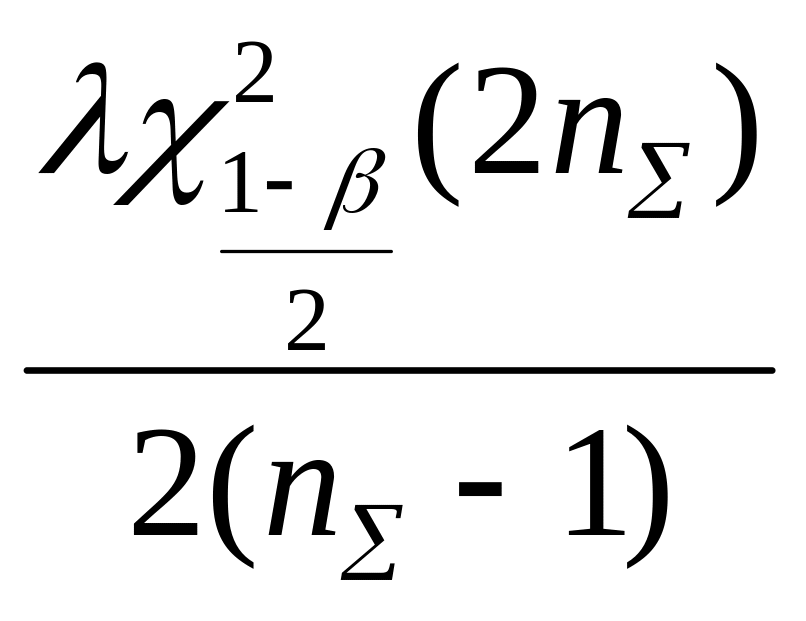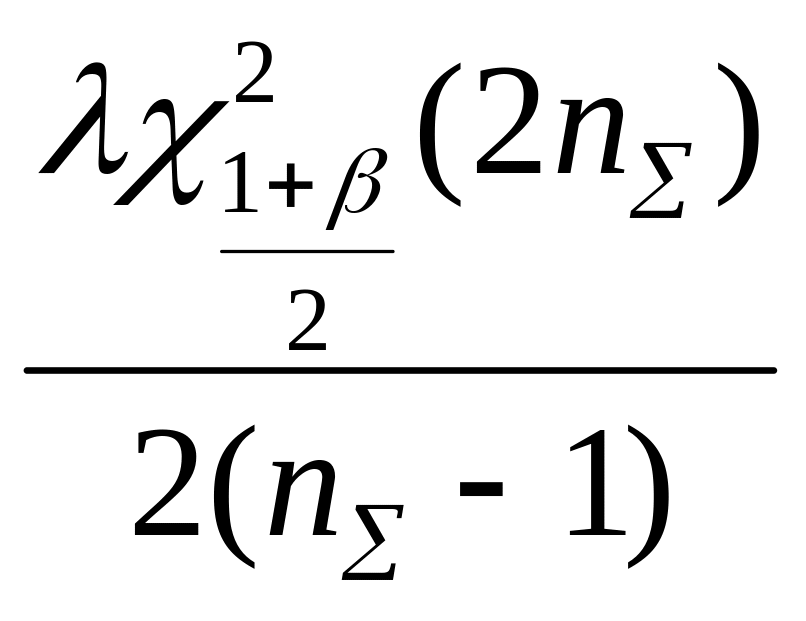- •Раздел 1 Основные термины и определения теории надёжности
- •1.1 Объект, система и элементы
- •1.2 Состояния и события
- •Постепенные – это отказы, которые наступают в результате длительного, постепенного изменения одного или нескольких параметров объекта.
- •1.3 Наработка и ресурс
- •1.4 Надежность
- •Раздел 2 Показатели надежности невосстанавливаемых объектов
- •2.1 Функции распределения и надёжности наработки до отказа
- •2.2 Плотность распределения наработки до отказа
- •2.3 Вероятности отказа и безотказной работы
- •2.4 Интенсивность отказов
- •2.5 Средняя наработка до отказа
- •Раздел 3 Законы распределения наработки до отказа
- •3.1 Экспоненциальное распределение
- •3.2 Нормальное распределение (распределение Гаусса)
- •3.3 Усечённое нормальное распределение
- •3.4 Логарифмически нормальное (логнормальное) распределение
- •3.5 Распределение Рэлея
- •3.6 Распределение Вейбулла
- •3.7 Гамма-распределение
- •3.8 Смесь распределений
- •Раздел 4 Потоки отказов и показатели надежности восстанавливаемых объектов
- •4.1 Понятие потока отказов. Простейший (пуассоновский) поток
- •4.2 Показатели безотказности
- •4.3 Показатели ремонтопригодности
- •4.4 Показатели долговечности
- •4.5 Комплексные показатели надежности
- •Раздел 5 Расчёт надёжности систем без учёта восстановления Расчёт надёжности системы – это определение её показателей надёжности по известным показателям надёжности элементов.
- •5.1 Основные этапы расчёта надежности
- •5.2 Способы соединения элементов и составление структурной схемы системы
- •5.3 Методы расчета надёжности невосстанавливаемых систем
- •5.3.1 Расчет надежности систем с последовательным и параллельным соединением элементов
- •5.3.2 Расчёт надёжности систем со сложной структурой
- •6.4 Резервирование систем
- •Раздел 6 Расчёт надёжности систем с учётом восстановления
- •6.1 Граф состояний системы
- •6.2 Расчет надежности восстанавливаемой системы с помощью уравнений типа массового обслуживания
- •6.3 Матрица состояний
- •6.3 Расчет надежности восстанавливаемой системы с помощью интегральных уравнений
- •Раздел 7 Оценка надёжности объектов по результатам испытаний
- •7.1 Виды испытаний на надежность
- •7.2 Определительные испытания
- •8.3 Контрольные испытания
- •Раздел 9 Обеспечение надёжности систем при эксплуатации
- •9.1 Организация эксплуатации
- •9.2 Классификация запасных частей
- •9.3 Организация пополнения запаса
- •9.4 Расчет числа невосстанавливаемых запасных частей с периодическим пополнением по вероятности достаточности
- •9.5 Расчет количества восстанавливаемых запасных частей по вероятности достаточности
- •9.6 Техническое обслуживание
- •Раздел 10 Диагностика автоматизированных систем
- •10.1 Классификация видов диагностирования
- •10.2 Классификация методов диагностирования
- •10.3 Показатели диагностирования
- •10.4 Математические модели объектов диагностирования
- •10.5 Системы технического диагностирования
- •10.6 Таблица функций неисправностей (тфн)
- •10.7 Алгоритмы диагностирования
- •Раздел 11 Анализ надежности программного обеспечения
- •11.1 Основные понятия надежности программного обеспечения
7.2 Определительные испытания
Планы
испытаний.
План испытаний -
это правила, устанавливающие объем
выборки, порядок проведения испытаний
и критерии их прекращения. Наименование
плана принято обозначать тремя буквами
(цифрами): первая из них обозначает число
испытываемых объектов, вторая – наличие
![]() или отсутствие
или отсутствие
![]() восстановлений на время испытаний в
случае отказа, третья – критерий
прекращения испытаний. Если объекты
подвергаются испытаниям одновременно,
то полученное обозначение плана испытаний
записывается в квадратных скобках. В
ряде случаев, испытания объектов могут
производится неодновременно и прекращаться
в произвольный момент по каким-либо
посторонним причинам, тогда план
испытаний записывается в круглых
скобках.
восстановлений на время испытаний в
случае отказа, третья – критерий
прекращения испытаний. Если объекты
подвергаются испытаниям одновременно,
то полученное обозначение плана испытаний
записывается в квадратных скобках. В
ряде случаев, испытания объектов могут
производится неодновременно и прекращаться
в произвольный момент по каким-либо
посторонним причинам, тогда план
испытаний записывается в круглых
скобках.
Рассмотрим наиболее типовые планы определительных испытаний.
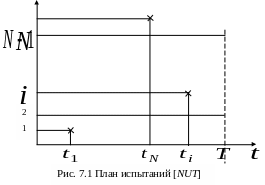
План [NUT] соответствует одновременному испытанию N объектов. Эти объекты после отказа не восстанавливаются (или же восстанавливаются, но данные о их поведении после первого отказа в испытаниях не рассматриваются). Испытания прекращают по истечении наработки каждого отказавшего объекта. На рис. 7.1 звёздочкой обозначено наличие отказа; – наработка до отказа -го объекта. Этот план обычно применяют для определения вероятности безотказной работы объекта за время T.
План
[NUr]
соответствует испытаниям
невосстанавливаемых объектов, однако
в отличие от плана [NUT]
испытания прекращают, когда число
отказавших объектов достигает
![]() .
В примере плана, данного на рис. 7.2,
-й
отказ имеет место у
-го
объекта. Если
.
В примере плана, данного на рис. 7.2,
-й
отказ имеет место у
-го
объекта. Если
![]() ,
то переходим к плану [NUN],
когда испытания прекращают после отказов
всех объектов. План [NUr]
обычно применяют для определения средней
наработки на отказ и средней наработки
до отказа в случае экспоненциального
распределения, а план [NUN]
-
в случае нормального распределения.
Испытания по плану [NUN]
требуют значительного времени и большого
числа испытываемых объектов, но дают
возможность полностью определить
функцию распределения. Планы [NUr]
и [NUT]
позволяют определить функцию распределения
только для некоторого интервала времени,
дают меньше информации, зато позволяют
быстрее закончить испытания.
,
то переходим к плану [NUN],
когда испытания прекращают после отказов
всех объектов. План [NUr]
обычно применяют для определения средней
наработки на отказ и средней наработки
до отказа в случае экспоненциального
распределения, а план [NUN]
-
в случае нормального распределения.
Испытания по плану [NUN]
требуют значительного времени и большого
числа испытываемых объектов, но дают
возможность полностью определить
функцию распределения. Планы [NUr]
и [NUT]
позволяют определить функцию распределения
только для некоторого интервала времени,
дают меньше информации, зато позволяют
быстрее закончить испытания.

План [NRT] описывает испытания N объектов, причем отказавшие во время испытаний объекты, подлежат восстановлению. Испытания прекращают по истечении наработки T каждой из N позиций (рис. 7.3).

Рис.
7.3
План испытаний [NRT]
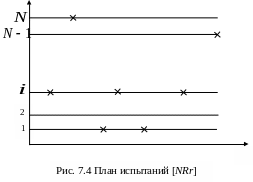
План [NRr] соответствует испытаниям N объектов, отказавшие во время испытаний объекты восстанавливают. Испытания прекращают, когда суммарное по всем позициям число отказавших объектов достигает r (рис. 7.4).
Задачами планирования является определение минимального объема наблюдений - выбор числа испытываемых объектов N, а также продолжительности наблюдений T для планов [NUT] и [NRT] или числа отказов r для планов [NUR] и [NRr].
Результатами определительных испытаний должны являться точечные и интервальные оценки показателей надежности.
Точечная оценка – это оценка, имеющая конкретное числовое значение, вычисляемое на основе наблюдений, и предположительно близкое оцениваемому параметру. Наиболее распространенной точечной оценкой является среднее арифметическое значение параметра.
Точечная оценка средней наработки до отказа
![]() (7.1)
(7.1)
соответствует плану [NUN], так как здесь рассматриваются завершенные (не прерванные в испытаниях) наработки до отказа каждого из испытываемых объектов. Это соотношение имеет место при любых законах распределения наработки до отказа.
Для экспоненциального распределения при всех рассмотренных планах испытаний, кроме плана [NUN] точечная оценка средней наработки до отказа
![]() ,
(7.2)
,
(7.2)
где
S
– суммарная наработка всех объектов
за время испытаний;
![]() суммарное
числе отказов всех объектов за время
испытаний.
суммарное
числе отказов всех объектов за время
испытаний.
При плане [NUT]
![]() ,
(7.3)
,
(7.3)
где l– число объектов, отказавших в интервале (0;T); наработка до отказа i-го объекта из числа отказавших.
При плане испытаний [NUr]
![]() .
(7.4)
.
(7.4)
Для
плана [NRT]
и простейшего потока, у которого время
между отказами подчиняется экспоненциальному
распределению, оценка
![]() средней наработки до отказа совпадает
с оценкой
средней наработки до отказа совпадает
с оценкой
![]() средней наработки на отказ
средней наработки на отказ
![]() .
(7.5)
.
(7.5)
Оценка интенсивности отказов
![]() при экспоненциальном распределении
может быть определена через оценку
средней наработки до отказа
при экспоненциальном распределении
может быть определена через оценку
средней наработки до отказа
![]() .
(7.6)
.
(7.6)
При плане [NUN]
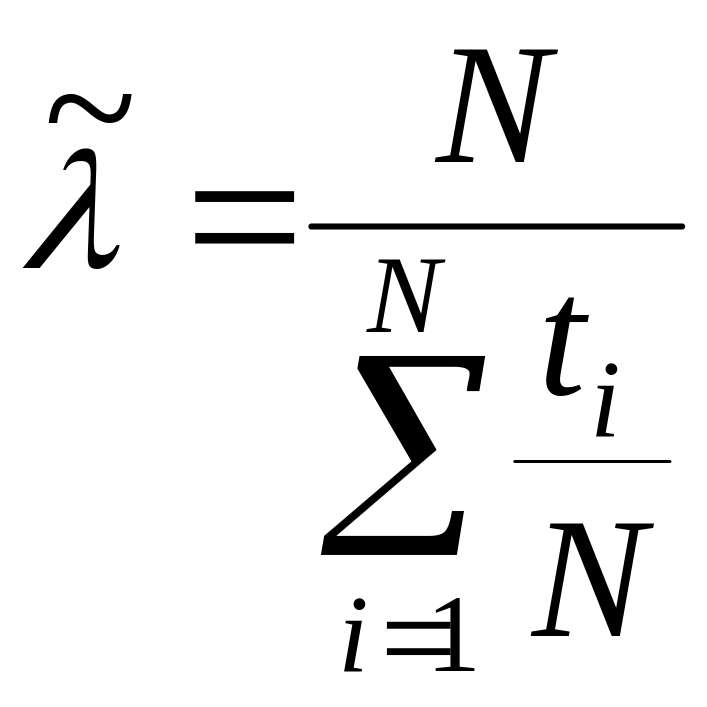 .
(7.7)
.
(7.7)
Оценка
параметра
![]() простейшего потока совпадает с оценкой
интенсивности отказов
.
При плане [NRT]
простейшего потока совпадает с оценкой
интенсивности отказов
.
При плане [NRT]
![]() .
(7.8)
.
(7.8)
При
нормальном распределении, кроме оценки
средней наработки до отказа, проводимой
по соотношению (7.1), часто требуется
найти точечную оценку и второго параметра
этого распределения, именно среднее
квадратическое отклонение
![]() .
При плане [NUN]
.
При плане [NUN]
![]() .
(7.9)
.
(7.9)
Оценка
среднего времени восстановления
определяется аналогично (7.1) и соответствует
плану [NUN].
Оценки вероятности отказа
![]() и вероятности безотказной работы
и вероятности безотказной работы
![]() до момента
до момента
![]() могут быть найдены за ограниченный
интервал времени
могут быть найдены за ограниченный
интервал времени
![]() и соответствуют плану испытаний [NUT].
и соответствуют плану испытаний [NUT].
Точечные оценки дают представление о значении показателя надежности, но ничего не говорят о точности этой оценки. Для рассмотрения точности оценки вводится понятие интервальной оценки.
Интервальная оценка – это оценка представляемая интервалом значений, внутри которого с определенной вероятностью находится истинное значение оцениваемого параметра. Интервал в интервальной оценке называется доверительным интервалом, а вероятность нахождения истинного значения оцениваемого параметра называется доверительной вероятностью. Доверительный интервал характеризуется нижней и верхней доверительными границами.
Некую
величину
![]() называют нижней
доверительной границей
параметра T
при односторонней доверительной
вероятности
называют нижней
доверительной границей
параметра T
при односторонней доверительной
вероятности
![]() ,
если параметр T
лежит на интервале
,
если параметр T
лежит на интервале
![]() с вероятностью
.
с вероятностью
.
Некую
величину
![]() называют верхней
доверительной границей
параметра T
при односторонней доверительной
вероятности
называют верхней
доверительной границей
параметра T
при односторонней доверительной
вероятности
![]() ,
если параметр T
лежит на интервале
,
если параметр T
лежит на интервале
![]() с вероятностью
.
с вероятностью
.
Наиболее часто используемые в задачах квантили распределения приведены в табл. 7.2.
Таблица 7.1
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Доверительные
границы
![]() и
и
![]() интенсивности отказов при экспоненциальном
распределении и различных планах
испытаний представлены в табл. 7.2.
интенсивности отказов при экспоненциальном
распределении и различных планах
испытаний представлены в табл. 7.2.
Таблица 7.2
План испытаний |
Интенсивность
отказов
или параметр потока отказов
|
|
Нижняя граница |
Верхняя граница |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Примечание.
![]() квантиль
квантиль
![]() распределения
при вероятности
распределения
при вероятности
![]() с
числом степеней свободы
с
числом степеней свободы
![]() ;
;
![]() суммарное
число отказов в испытаниях.
суммарное
число отказов в испытаниях.
Для
восстанавливаемых объектов при простейшем
потоке отказов доверительные границы
параметра потока отказов
![]() ,
,
![]() .
Нижняя и верхняя доверительные границы
средней наработки до отказа и средней
наработки на отказ соответственно будут
.
Нижняя и верхняя доверительные границы
средней наработки до отказа и средней
наработки на отказ соответственно будут
![]() ;
;
![]() .
(7.10)
.
(7.10)
За
заданное время
![]() нижняя и верхняя доверительные границы
вероятности безотказной работы
нижняя и верхняя доверительные границы
вероятности безотказной работы
![]() ;
;
![]() .
(7.11)
.
(7.11)
Если
в результате испытаний по плану [NRT]
число отказов равно нулю, то
![]() .
При этом определяется только односторонняя
верхняя доверительная граница
.
При этом определяется только односторонняя
верхняя доверительная граница
![]() .
(7.16)
.
(7.16)
где
![]() – квантиль
– квантиль
![]() – распределения при вероятности
с числом степеней свободы 2;
– распределения при вероятности
с числом степеней свободы 2;
![]() .
.