Доверительный интервал для математического ожидания

Пусть по выборке достаточно большого объема, n > 30, и при заданной доверительной вероятности 1–  необходимо определить доверительный интервал для математического ожидания m₁, в качестве оценки которого используется среднее арифметическое .

Закон распределения оценки математического ожидания близок к нормальному (распределение суммы независимых случайных величин с конечной дисперсией асимптотически нормально). Если потребовать абсолютную надежность оценки математического ожидания, то границы доверительного интервала будут бесконечными [–  ,  ]. Выбор любых более узких границ связан с риском ошибки, вероятность которой определяется уровнем значимости  . Интерес представляет максимальная точность оценки, т.е. наименьшее значение интервала. Для симметричных функций минимальный интервал тоже будет симметричным относительно оценки  ₁. В этом случае выражение для доверительной вероятности имеет вид P(|  ₁ – m₁ |  Е)=1– , где Е – абсолютная погрешность оценивания.

Нормальный закон полностью определяется двумя параметрами – математическим ожиданием и дисперсией. Величина  ₁ является несмещенной, состоятельной и эффективной оценкой математического ожидания, поэтому ее значение принимаем за значение математического ожидания. Определим оценку дисперсии случайного параметра  ₁, учитывая, что этот параметр равен среднему арифметическому одинаково распределенных случайных величин x_i (следовательно, их дисперсии D(x_i) одинаковы и равны  ₂)

.

Итак, случайная величина  ₁ распределена по нормальному закону с параметрами  ₁ и  ₂ / n. Для установления необходимых соотношений целесообразно перейти к центрированным и нормированным величинам. Выражение  ₁ – m₁ можно трактовать как центрирование случайной величины  ₁. Нормирование осуществляется делением на величину среднеквадратического отклонения оценки  ₁

.

Для стандартизованной величины вероятность соблюдения неравенства определяется по функции нормального распределения

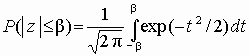= Ф( ) – Ф(– ) = –1+ 2Ф( )=1–  ,

где . Значение  равно квантили u_{1–  /2} стандартного нормального распределения уровня 1–  /2. В частности, уровням надежности 0,9, 0,95 и 0,99 соответствуют значения допустимого отклонения u_{1–  /2} величины z, равные 1,64, 1,96 и 2,58 соответственно. Окончательно можно записать

u ²_{1–  /2} = nЕ²/ ₂ .

Доверительный интервал для дисперсии

По выборке достаточно большого объема (n>30) и при заданной надежности 1–  необходимо определить доверительный интервал для дисперсии m₂ , оценка которой .

Если стандартизовать оценку дисперсии, то величина (n–1) ²/m₂ имеет распределение хи-квадрат с (n–1) степенями свободы. Из этого вытекает вероятностное утверждение относительно выборочной дисперсии

P[(n–1) ² /m₂ >^2 (n–1)] =  .

Функция хи-квадрат несимметричная,поэтому границы интервала ²₁(n–1)и  ²₂(n–1) выбирают из условия равной вероятности выхода за их пределы P[(n–1) ²/m₂ < ²₁(n–1)] = P[(n–1) ²/m₂ > ²₂(n–1)] =  /2 или

P[(n–1) ²/ ²₁(n–1) < m₂] = P[(n–1) ²/ ²₂(n–1) > m₂] =  /2.

Значения границ соответствуют квантилям распределения хи-квадрат уровня  /2 и 1–  /2 с количеством степеней свободы n–1. Нижняя граница  ²₁(n–1) равна квантили ^{2 } _/2(n–1), а верхняя – квантили  ²_{1– /2}(n–1). Если воспользоваться критическими точками распределения, то следует записать  ²₁(n–1) =  ²(1–  /2; n–1) и  ²₂(n–1) =  ²( /2; n–1).