27. Общее решение линейных рекуррентных соотношений второго порядка с постоянными коэффициентами (случай одинаковых корней характеристического уравнения). Привести примеры.

Линейные рекуррентные соотношения с постоянными коэффициентами

Для решения рекуррентных соотношений общих правил, вообще говоря, нет. Однако существует весьма часто встречающийся класс соотношений, решаемый единообразным методом. Это - рекуррентные соотношения вида

(8.3)

где - некоторые числа. Такие соотношения называют линейными рекуррентными соотношениями с постоянными коэффициентами.

Сначала рассмотрим, как решаются такие соотношения при , то есть изучим соотношение вида

(8.4)

Решение этих соотношений основано на следующих двух утверждениях.

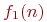1. Если и 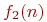являются решениями рекуррентного соотношения (8.4), то при любых числах 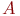и 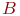последовательность 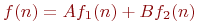также является решением этого соотношения.

В самом деле, по условию, имеем

Умножим эти равенства на и соответственно и сложим полученные тождества. Получим, что

А это означает, что является решением соотношения(8.4).

2. Если 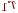является корнем квадратного уравнения

то последовательность

является решением рекуррентного соотношения

В самом деле, если , то и . Подставляя эти значения в соотношение (8.4), получаем равенство

Оно справедливо, так как по условию имеем . Заметим, что наряду с последовательностью любая последовательность вида

также является решением соотношения (8.4). Для доказательства достаточно использовать утверждение (8.4), положив в нем .

Из утверждений 1 и 2 вытекает следующее правило решения линейных рекуррентных соотношений второго порядка с постоянными коэффициентами.

Пусть дано рекуррентное соотношение

(8.5)

Составим квадратное уравнение

(8.6)

которое называется характеристическим для данного соотношения. Если это уравнение имеет два одинаковых корня, , то выражение уже не будет общим решением(как это было в случае когда r1 неравно r2). Из-за того, что , это решение можно записать в виде

Остается только одно произвольное постоянное ; и выбрать его так, чтобы удовлетворить двум начальным условиям , вообще говоря, невозможно.Поэтому надо найти какое-нибудь второе решение, отличное от . Таким решением является . В самом деле, если квадратное уравнение имеет два совпадающих корня , то по теореме Виета . Поэтому уравнение записывается так:

А тогда рекуррентное соотношение имеет такой вид:

(8.10)

Проверим, что действительно являются его решением. Имеем , а . Подставляя эти значения в соотношение (8.10), получаем очевидное тождество

Значит, - решение рассматриваемого соотношения.

Итак, имеются два решения и заданного соотношения. Его общее решение запишется так:

Теперь уже путем подбора можно удовлетворить любым начальным условиям.

Линейные рекуррентные соотношения с постоянными коэффициентами, порядок которых больше двух, решаются таким же способом. Пусть соотношение имеет вид

(8.11)

Составим характеристическое уравнение

Если все корни этого алгебраического уравнения -й степени различны, то общее решение соотношения (8.3) имеет вид

Если же, например, , то этому корню соответствуют решения

рекуррентного соотношения (8.11). В общем решении этому корню соответствует часть

Составляя такое выражение для всех корней и складывая их, получаем общее решение соотношения (8.3).

Например, решим рекуррентное соотношение

Характеристическое уравнение в этом случае имеет вид

Решая его, получим корни

Значит, общее решение нашего соотношения имеет следующий вид: