2) Напряженность электрического поля в диэлектрике
Рассмотрим
диэлектрическую пластинку, заполняющую
плоский конденсатор (рис.14.5) и находящуюся,
следовательно, в практически однородном
внешнем поле 
.
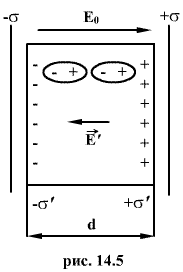
В
результате поляризации на гранях
диэлектрика, обращенных к пластинам
конденсатора, концы молекулярных диполей
окажутся нескомпенсированными соседними
диполями. Поэтому на правой грани,
обращенной к отрицательной пластине
конденсатора, окажется избыток
положительного заряда с некоторой
поверхностной плотностью 
.
На противоположной стороне диэлектрика 
.
Эти так называемые поляризационные,
или связанные заряды не могут быть
переданы соприкосновением другому телу
без разрушения молекул диэлектрика,
т.к. они обусловлены самими поляризованными
молекулами. Возникновение поляризованных
зарядов приводит к возникновению
дополнительного электрического поля
,
направленного против внешнего поля
.
Результирующее электрическое поле Е
внутри диэлектрика равно
|
(14.2) |
Для
определения 
применим
формулу вычисления напряженности 
конденсатора
|
(14.3) |
Свяжем 
с
вектором поляризации Р. Для этого
определим полный дипольный момент (во
всем объеме) диэлектрика. Осуществим
это двумя способами:
С одной стороны Р по определению дипольный момент единицы объема и если умножим на V, получим полный дипольный момент
|
(14.4) |
где S - площадь пластины конденсатора.
С другой стороны рассмотрим диэлектрик как большой диполь, у которого с одной стороны заряд , а с другой и расстояние d. Отсюда
|
(14.5) |
Приравнивая (14.4) и (14.5), получим
Подставляя в (14.3), и затем результат в (14.2), получим
Подставим значение Р из выражения (14.1), тогда
|
(14.6) |
Величина
|
(14.7) |
называется
диэлектрической проницаемостью или
относительной диэлектрической
проницаемостью. Диэлектрическая
проницаемость
показывает
во сколько раз уменьшается напряженность
в диэлектрике по сравнению с напряженностью
в вакууме.
и 
,
т.е. с ростом температуры диэлектрические
свойства ухудшаются.
3) Электрическое смещение
В неоднородной диэлектрической среде имеет различные значения, изменяясь на границах диэлектриков скачкообразно (претерпевая разрыв). Это затрудняет применение формул, описывающих взаимодействие зарядов в вакууме. Что касается теоремы Гаусса, то в этих условиях она вообще теряет смысл. В самом деле, благодаря различной поляризуемости разнородных диэлектриков напряженности поля в них будут различными. Поэтому различно и число силовых линий в каждом диэлектрике (рис.14.6).
Часть
линий, исходящих из зарядов, окруженных
замкнутой поверхностью, будет заканчиваться
на границе раздела диэлектриков и не
пронижет данную поверхность. Это
затруднение можно устранить, введя в
рассмотрение новую физическую
характеристику поля – вектор электрического
смещения
|
(14.8) |
Вектор направлен в ту же сторону, что и . В отличие от напряженности поля вектор имеет постоянное значение во всех диэлектриках. Поэтому электрическое поле в неоднородной диэлектрической среде удобнее характеризовать не напряженностью , а смещением . С этой целью вводится понятие линий вектора и потока смещения, аналогично понятию силовых линий и потока напряженности
или
|
(14.9) |
Используя теорему Гаусса
домножим
обе части на 
С учетом (14.8) получаем
|
(14.10) |
Это уравнение выражает теорему Гаусса для вектора электрического смещения: полный поток вектора электрического смещения через произвольную замкнутую поверхность равен сумме свободных зарядов, заключенных в этой поверхности.