
- •1. Световые волны в прозрачной изотропной среде.
- •Частные решения волнового уравнения.
- •Параметры плоской волны.
- •Фазовая скорость.
- •Групповая скорость.
- •Поперечность световых волн.
- •11.2. Гармоническая волна
- •11.3. Волны в пространстве
- •11.4. Плоские электромагнитные волны *
- •11.5. Плоская гармоническая электромагнитная волна
- •Плоские электромагнитные волны Понятие электромагнитной волны.
- •Поперечный характер электромагнитных волн.
- •Фазовая и групповая скорости электромагнитной волны.
- •11.6. Интенсивность волны
- •11.7. Отражение электромагнитной волны от границы раздела двух сред
- •Понятие интерференции электромагнитных волн
- •Интерференция света
- •12.2. Когерентность
- •12.3. Интерференция света от двух точечных источников
- •12.4. Интерференция света в тонких пленках
- •13 * Дифракция
- •13.1. Принцип Гюйгенса — Френеля
- •13.3. Дифракция света на круглом отверстии
- •13.4. Дифракция света на щели
- •13.5. Дифракционная решетка
- •14. Поляризация света
- •14.1. Поляризация электромагнитной волны
- •14.2. Естественный и поляризованный свет
- •14.3. Поляризация света при отражении и преломлении
- •14.4. Поляризация света при двойном лучепреломлении
- •14.6. Интерференция поляризованных лучей
- •15. * Взаимодействие света с веществом
- •15.1. Дисперсия света
- •15.2. Электронная теория дисперсии
- •15.3. Групповая скорость волны
- •3.1. Возникновение волны. Группа волн
- •15.4. Поглощение света
- •Краткое математическое содержание волновой оптики
- •1. Световые волны в прозрачной изотропной среде.
- •Тема 2. Поляризация света.
- •Тема 3. Излучение и поглощение света.
- •Тема 4. Отражение и преломление света.
- •Тема 5. Кристаллооптика.
- •Тема 6. Геометрическая оптика.
- •Тема 7. Спектр света.
- •Тема 8. Интерференция.
- •Тема 9. Дифракция.
- •Тема 10. Дифракционная решетка.
- •Тема 11. Голография.
- •Тема 12. Дифракционный предел разрешения.
- •Тема 13. Взаимодействие света с веществом.
- •Тема 14. Термодинамика излучения.
11.6. Интенсивность волны
Рассмотрим распространяющуюся вдоль оси у плоскую гармоническую электромагнитную волну, которая описывается функциями (11.32) и (11.33). По формулам (10.11) и (10.12) найдем плотность энергии электромагнитного поля и вектор Умова - Пойнтинга:
S = EmHmj cos2(wt-k y -a). (11.34)
Nспользуя соотношение (11.30), получаем:
w = ε Е2m cos2(w t- к у + a),
где j - единичный вектор, направленный вдоль оси у.
Отметим, что в силу соотношения (11.30) плотности энергии электрического и магнитного полей равны друг другу. Направление вектора 5 плотности потока энергии, как видно из формулы (11.35), совпадает с направлением волнового вектора к, т.е. направление, в котором распространяется энергия электромагнитного поля, совпадает с направлением распространения волны. Плотность энергии w и вектор S зависят от времени и координат. Амплитуды колебаний этих величин
wm = ε Е2m , Sm= (1/2) √ε/μ Е2m
связаны друг с другом простым соотношением
Sm = v wm .
Формулу (11.27), которая определяет скорость v распространения электромагнитной волны, можно записать так:
v=1/![]() =1/
=1/![]()
v=c/n
Здесь εr и μr - относительные диэлектрическая и магнитная проницаемости среды, в которой движется электромагнитная волна,
c=1/![]()
- скорость электромагнитных волн в пустоте, а величина
п = .
называется показателем преломления среды. Относительная магнитная проницаемость всех прозрачных для электромагнитных волн веществ практически равна единице: μr ~ 1. Поэтому
n=√εr (11.38)
Из формулы (11.37) следует, что скорость электромагнитных волн в среде в п раз меньше их скорости в пустоте.
Среднее по времени значение абсолютной величины вектора плотности потока энергии называется интенсивностью волны:
I=
![]()
где Т - период волны. Согласно этому определению, размерность и физический смысл интенсивности те же, что и величины S. Подставим в формулу (11.39) выражение (11.35) для модуля вектора Умова - Пойнтинга. После интегрирования получим
![]()
Интенсивность — плотность потока энергии (энергия в единицу времени через единицу площади).
(среднее по времени от вектора плотности потока энергии)
Связь интенсивности света с объемной плотностью энергии световой волны.
, где — фазовая скорость света, хотя казалось бы, должна быть групповая.
С учетом соотношения (11.37) будем иметь

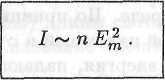
11.7. Отражение электромагнитной волны от границы раздела двух сред
Пусть плоская электромагнитная волна падает перпендикулярно на плоскость, разделяющую две среды с показателями преломления n1 и п2 (рис. 11.5). На границе раздела сред волна делится на две волны. Одна волна проходит через границу раздела из первой среды во вторую, а другая отражается и движется в первой среде навстречу падающей волне. Напряженности электрического поля и волновые векторы в падающей, отраженной и прошедшей во вторую среду волн обозначим соответственно E1 k1 Е1' к1' и Е2 к2
Из уравнений Максвелла следует, что тангенциальные составляющие вектора Е напряженности электрического поля не изменяются при переходе через границу раздела двух сред:
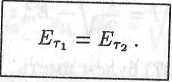
(11.41)
Направим ось х вдоль вектора Е1. В таком случае это граничное условие принимает вид
EXl+ ЕХ1' = ЕХ2
(11.42)
где EXl, ЕХ1' и ЕХ2 - проекции на ось х векторов Е1, Е1', и Е2 соответственно. Сумма в левой части равенства (11.42) - напряженность электрического поля в первой среде. По принципу суперпозиции она равна сумме напряженностей полей падающей и отраженной волн.
n1 Е1, к1' Е1'

п2 к1 к2. Е2,
Рис. 11.5. Падение волны на границу раздела двух сред
В силу формулы (11.35) энергия, падающая за единицу времени на единицу площади, пропорциональна показателю преломления и квадрату напряженности электрического поля волны:
S~nE2.
Учитывая это соотношение, запишем равенство
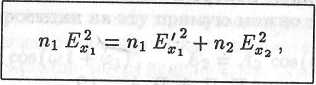
которое означает, что плотность потока энергии падающей волны равна сумме плотностей потоков энергии отраженной и прошедшей во вторую среду волн. Из уравнения (11.42) найдем, что
ЕХ1'=ЕХ2-ЕХ1. (11.44)
Исключив величину ЕХ1' из (11.43) при помощи этой формулы, придем к равенству
n1 Ex12 = n1(Ех2 -EXl)2 + n2 Ex22 .
Отсюда следует, что напряженность ЕХ2 электрического поля в волне, прошедшей во вторую среду, связана напряженностью ЕХ1 поля в падающей волне соотношением
Ex2 =(2n1/(n1 +n2)) Ex1 (11.45)
Подставив (11.45) в (11.44), получим
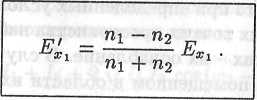
(11.46)
Формулы (11.45) и (11.46) определяют связь между напряженностями электрического поля падающей, отраженной и прошедшей волн.
Если первая среда является оптически менее плотной, т.е. n1 < n2, то из формулы (11.46) следует, что проекции ЕХ1' и EX1 имеют разные знаки. Это означает, что при отражении волны вектор напряженности электрического поля меняет направление на противоположное, т.е. векторы Е1' и Е1 на границе раздела направлены в разные стороны. Так как cos (φ+ π) = - cosφ, изменение направления вектора Е можно интерпретировать как результат изменения фазы на π, что эквивалентно уменьшению (или увеличению) длины светового луча на величину λ/2. Поэтому это явление носит название "потеря" полволны. При п1 > п2 векторы Е1' и Е1 совпадают по направлению.
4. ВОЛНОВАЯ ОПТИКА
12. ИНТЕРФЕРЕНЦИЯ
12.1. Сложение волн
Теоретически и экспериментально установлено, что электромагнитные волны распространяются в пространстве со скоростью света. На основании этого и многих других фактов пришли к заключению, что видимый свет есть электромагнитные волны. В этом и следующих разделах будут рассмотрены такие оптические явления, как интерференция, дифракция и поляризация, в которых свет проявляет свои волновые свойства.
Если две или несколько волн накладываются друг на друга в какой-то области пространства, то при определенных условиях возникает явление интерференции. В одних точках пространства наблюдается усиление колебаний, в других точках - их ослабление. В случае интерференции световых волн на экране, помещенном в области их наложения, возникает так называемая интерференционная картина, т.е. на экране наблюдается чередование темных и светлых пятен или полос.
Электромагнитную волну можно рассматривать как совокупость согласованных колебаний векторов напряженности электрического и магнитного полей в различных точках пространства. Пусть в некоторой области пространства распространяются две гармонические электромагнитные волны одной и той же частоты и. Эти волны можно описать посредством зависимостей напряженностей электрических полей этих волн от времени и координат:
![]()
= E2(t,r).
Согласно принципу суперпозиции напряженность электрического поля в
Произвольной точке Р пространства равна сумме напряженности полей,
создаваемых различными источниками электромагнитного излучения:
E = E1 + E2 . (12.2)
Предположим, что векторы E1 и Е2 в точке Р направлены вдоль одной прямой.
Тогда их проекции на эту прямую можно записать так:
E1= A1 cos(wt + φ1), Е2= A2 cos(wt + φ2), (12.3)
где A1 и А2 - амплитуды гармонических колебаний, создаваемых рассматриваемыми гармоническими волнами в точке Р; φ1 и φ2 - начальные фазы этих колебаний.
Как известно из теории гармонических колебаний, сумма
E(t) = E1(t) + E2(t) (12.4)
двух гармонических колебаний также будет гармоническим колебанием
Е= A cos(wt + φo) (12.5)
той же частоты ω, амплитуда А которого связана с амплитудами А1 и А2 суммируемых колебаний соотношением
(12.6)
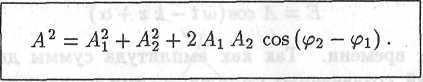
Так как интенсивность волны пропорциональна квадрату амплитуды, соотношение (12.6) можно переписать в виде
![]() (12.7)
(12.7)
где I- интенсивность света в точке Р, I1 и I2 интенсивности каждой из волн в отдельности.
Как следует из формулы (12.7), результирующая интенсивность I в общем случае не равна сумме I1 + I2 интенсивностей складываемых волн. Она может быть как больше, так и меньше ее в зависимости от последнего слагаемого в выражении (12.7), называемого интерференционным членом. Интерференционный член зависит от разности фаз φ2 - φ1. В тех точках пространства, для которых
φ2 - φ1 =2πm , (12.8)
где m = 0, ±1, ±2,...; колебания будут усиливать друг друга. В этих точках
cos (φ2 - φ1 ) = 1
и, как следует из формул (12.6) и (12.7), амплитуда А и интенсивность I принимают наибольшие значения:
Атах=А1+А2, Imax = (√I1 +√ I2)2 (12.9)
В точках, для которых
φ2 - φ1 =(2m+1)π , (12.10)
где m = 0, ±1, ±2,...;
cos (φ2 - φ1 ) = - 1.
При этом формулы (12.6) и (12.7) дают наименьшие значения амплитуды
и интенсивности:
Атin=|А1-А2|, Imin = (√I1 -√ I2)2
