Тема 5. Кристаллооптика.

Факультативно. Механизм замедления света в среде.

Свет, проходя через среду, раскачивает электрические диполи атомов. Излучение диполей складывается с проходящей мимо световой волной, в результате сложения получается волна с измененной фазой. Изменение фазы относительно волны в вакууме означает другую фазовую скорость света в среде. В анизотропной среде для разных направлений вектора различается величина наведенного электрического диполя и изменение фазы световой волны. В результате оказывается, что скорость света в кристалле зависит не от направления луча, а от направления вектора в световой волне.

Факультативно. Главные диэлектрические оси кристалла.

По определению вектора электрической индукции , где — поляризация среды или объемная плотность дипольного момента. Если дипольные моменты пропорциональны полю , то и вектор пропорционален . Для анизотропной среды коэффициент пропорциональности является симметричной матрицей .

или , где — условие симметричности матрицы .

Поворотом системы координат симметричную матрицу всегда можно привести к диагональному виду: .

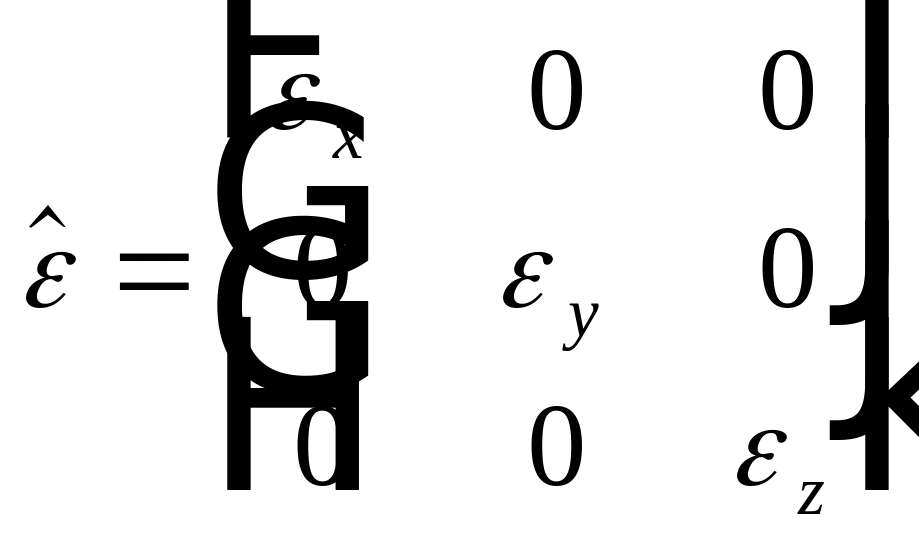Оси, в которых матрица — диагональная называются главными диэлектрическими осями кристалла. Не путать с осями кристалла, о которых речь пойдет ниже.

Факультативно. Аналог волнового уравнения в кристалле.

=>

, но

, тогда

Направления векторов , , , , , плоской световой волны в кристалле.

Для любой плоской волны получаем . Тогда уравнения Максвелла можно записать в виде , откуда получаем и, учитывая для вектора Пойнтинга, из трех последних равенств системы и равенства для вектора Пойнтинга получаем . Кроме того, из 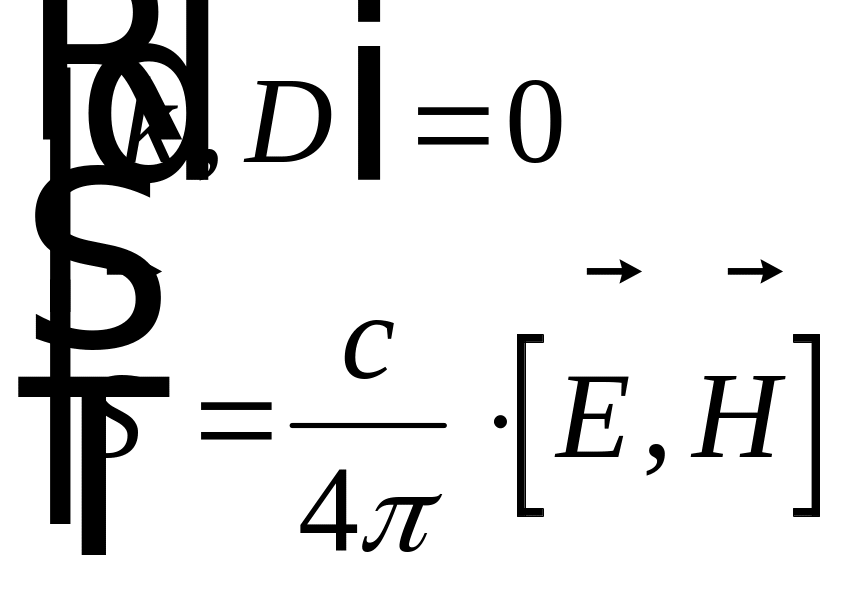получаем . Следовательно, тройка векторов , , — взаимно ортогональна и тройка векторов , , — взаимно ортогональна.

Тогда векторы , , , ортогональны вектору , а угол между векторами и равен углу между векторами и .

Лучевая и фазовая скорости световой волны в кристалле.

Обе скорости являются аналогом фазовой скорости света в изотропной среде. Лучевая скорость световой волны в кристалле определяется направлением распространения энергии и совпадает с направлением вектора Пойнтинга , где — объемная плотность энергии электромагнитного поля световой волны.

Фазовая скорость световой волны — скорость движения поверхности с постоянным значением фазы. — фаза любой волны. Выберем ось z в направлении вектора световой волны. , тогда и уравнение постоянной фазы примет следующий вид . Продифференцируем это уравнение по времени и получим , откуда . Окончательно для фазовой скорости

и .

Рассматривая перемещение поверхности равных фаз можно получить

, где — угол между векторами и , и он же угол между векторами и .

Факультативно. Величина лучевой и фазовой скорости в простейшем случае.

Простейший случай — это когда направление вектора световой волны совпадает с одной из главных диэлектрических осей кристалла (пусть с осью x). В главных диэлектрических осях связь векторов и выглядит достаточно просто . Откуда получаем . Если вектор направлен вдоль оси x, то , откуда вектор тоже имеет только составляющую . Следовательно, в рассматриваемом случае векторы и сонаправлены и кристаллическая среда ведет себя аналогично изотропной среды. Величина лучевой скорости в кристалле всегда зависит только от направления вектора , а не от направления света. Тогда — лучевая и фазовая скорости совпадают по величине и направлению (угол между лучевой и фазовой скоростями равен углу между векторами и , который равен нулю).

Фазовая пластинка.

Рассмотрим случай, когда свет распространяется вдоль одной из главных диэлектрических осей кристалла. Пусть . Поскольку , вектор лежит в плоскости x,y. Разложим вектор на составляющие вдоль осей x и y. Каждая из двух составляющих будет иметь вектор , направленный вдоль главной диэлектрической оси кристалла. Следовательно, каждая из двух составляющих поля будет иметь свою лучевую скорость, совпадающую с фазовой скоростью, . Для этих двух лучей показатели преломления не равны — двулучепреломление.

Фазовая пластинка — плоско параллельная кристаллическая пластинка, у которой две главные диэлектрические оси с различающимися диэлектрическими проницаемостями лежат в плоскости пластины.

Пластинки и .

Фазовая пластинка с оптической разностью хода для двух линейных поляризаций называется пластинкой .

Для пластинки разность хода — и соответственно .

Лучевой эллипсоид. Определение поляризации и лучевой скорости лучей по лучевому эллипсоиду (без доказательства).

Направим оси координат вдоль главных диэлектрических осей кристалла. Рассмотрим поверхность так называемого лучевого эллипсоида, уравнение которого . Главные полуоси эллипсоида имеют длины , , , равные лучевым скоростям, когда вектор направлен вдоль соответствующих осей.

Алгоритм нахождения поляризаций двух световых волн для заданного направления луча следующий. , поэтому векторы обеих волн лежат в плоскости перпендикулярной лучу. Рассмотрим сечение эллипсоида плоскостью перпендикулярной лучу , проходящей через центр эллипсоида. Сечение эллипсоида — эллипс. Оси эллипса — направления вектора двух лучей. Длина полуосей эллипса — лучевые скорости двух лучей.

Оптическая ось кристалла (лучевая ось). Одноосные и двуосные кристаллы.

Нельзя путать оси кристалла с главными диэлектрическими осями кристалла.

Кристаллы называются одноосными, если . Если , то кристалл двуосный.

Направление луча, для которого лучевая скорость любой поляризации света одинакова, называется осью кристалла (оптической осью, лучевой осью).

Если , то кристалл имеет две оси в плоскости x,z.

Обыкновенный и необыкновенный лучи.

В одноосном кристалле один луч обыкновенный, другой — необыкновенный. В двуосном кристалле оба луча необыкновенные.

Рассмотрим одноосный кристалл. Рассмотрим центральное сечение лучевого эллипсоида. Всегда одна из полуосей сечения перпендикулярна оси кристалла. Ее длина не зависит от направления плоскости сечения. Лучевая скорость соответствующего луча не зависит от направления луча. Это и есть обыкновенный луч. для луча этой поляризации кристалл изотропен.

Рассмотрим плоскопараллельную пластинку из одноосного кристалла. Пусть на пластинку под углом к нормали падает неполяризованный свет. При вращении пластинки вокруг нормали обыкновенный луч неподвижен, а необыкновенный луч на выходе из пластинки смещается параллельно самому себе.

Факультативно. Построение двойной лучевой поверхности с помощью лучевого эллипсоида.

Нельзя путать лучевую поверхность с рассмотренной ранее поверхностью лучевого эллипсоида.

Выберем в пространстве некоторую точку O, вокруг которой и будем строить лучевые поверхности. Для каждого направления луча отложим из одной и той же точки O два отрезка, равные лучевым скоростям двух лучей для выбранного направления луча. Величины лучевых скоростей двух лучей находятся как длины полуосей сечения лучевого эллипсоида плоскостью перпендикулярной выбранному направлению луча. Вторые концы двух отрезков при изменении направления луча образуют две лучевые поверхности.

Факультативно. Построения Гюйгенса в изотропной и анизотропной среде.

Лучевая скорость направлена в точку касания фронта волны лучевой поверхности.

Фазовая скорость направлена перпендикулярно фронту волны.

Поляризаторы на основе призмы Николя и Волластона.

Призма Николя. Две призмы из исландского шпата, склеены канадским бальзамом. , где n — показатель преломления канадского бальзама. Свет одной из линейных поляризаций испытывает на границе полное внутреннее отражение и выходит из рассмотрения. Свет, проходящий сквозь границу, будет линейно поляризован и слегка ослаблен.

Призма Волластона состоит из двух призм, в которых направления оси кристалла ортогональны. На границе двух призм свет двух линейных поляризаций преломляется отклоняясь в разные стороны.