15.3. Групповая скорость волны

При измерении скорости электромагнитной волны применяют мето­ды, в которых используют эффект запаздывания сигналов, посылаемых с этой волной. Сигнал посылается к некоторому объекту, расстояние г до которого известно. Измеряется время τ, по прошествии которого отраженный от объекта сигнал возвращается обратно. Скорость волны вычисляют по формуле

v=2l/τ

292

Что такое сигнал? Сигнал - это "метка", которую необходимо сделать на волне для того, чтобы определить момент времени, когда волна была отправлена к исследуемому объекту. Функция (15.5)

Е_у = Е_т cos(ωt- kx);

описывает идеальную гармоническую волну. Эта волна распространяет­ся бесконечно долго вдоль бесконечного луча. Такая волна не имеет на себе никаких "меток" и не может служить в качестве сигнала при изме­рении скорости волны. Сигналом может служить, например, "половина" гармонической волны, которая испускается генератором, начавшим ра­ботать в некоторый момент времени t_o. До этого момента генератор не работал. "Половина" гармонической волны уже не гармоническая волна. Волна сложной формы может быть представлена в виде суммы гармони­ческих волн. В самом простом случае в такой сумме будет только два слагаемых. Рассмотрим волну, которая является суперпозицией двух гармонических волн одинаковой амплитуды:

Е_у = Е_у⁽¹⁾+ Е_у⁽²⁾

Е_у⁽¹⁾= Е_т cos(ω₁t- k₁ x), Е_у⁽²¹⁾= Е_т cos(ω₂t- k₂x)

Преобразуем эту сумму при помощи тригонометрического тождества^

cos a + cos β = 2 cos( (a – β)/2)cos(( a +β)/2)

Получим следующее выражение:

Е_у = Е_т cos(((ω₂ - ω₁)t- (k₂-k₁) x )/2) cos(((ω₂ + ω₁)t- (k₂+k₁) x )/2);

Пусть частоты ω₂ , ω₁ волновые числа k₂,k₁ h езначительно отличаются друг

от друга, т.е. положим

ω₂ - ω₁ = 2 dω, k₂-k₁ = 2 dk ,

где dωi и dk - бесконечно малые величины. Полусуммы частот и волно­вых чисел обозначим так:

ω =(ω₂ + ω₁)/2 k=(k₂+k₁)/2

Теперь сумма двух гармонических волн принимает вид

Е_у =2 Е_т cos(dωt- dk x) cos(ωt- k x );

Это выражение представляет собой функцию от времени t и координаты х. График зависимости напряженности Е_у электрического поля от х при t = const показан на рис. 15.5.

E_y(x,t = const)

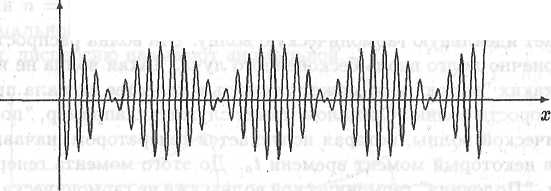
Рис. 15.5. Сумма двух гармонических волн

Волна, описываемая функцией (15.20), называется модулированной. Она содержит в себе две волны, одна из которых

A cos(ωt- k x ); (15.21)

называется несущей волной. Амплитуда

A=2 Е_т cos(dωt- dk x) (15.22)

также является волной. Эту волну называют модулирующей волной, или просто модуляцией. Модулирующая волна имеет частоту dω, которая очень мала по сравнению с частотой ω несущей волны. При этом длина модулирующей волны много больше длины несущей волны. Скорость несущей волны

v=ω /k (15.23)

называют фазовой скоростью, а скорость модулирующей волны

u=dω/dk

(15.24)

- групповой скоростью. Вообще говоря, эти скорости не совпадают.

Модулированная волна может служить сигналом, так как модулиру­ющая ее волна несет информацию. Эта информация распространяется вдоль луча с групповой скоростью и. Таким образом, при измерении скорости волны по времени запаздывания сигнала получают значение групповой скорости. Групповая скорость всегда меньше скорости света в пустоте, а фазовая скорость может быть даже больше скорости света.