15.2. Электронная теория дисперсии

Рассмотрим в общих чертах, как происходит взаимодействие электро­магнитных волн с веществом. Электрическое поле волны действует на заряженные частицы, из которых состоит вещество. Заметнее всего оно действует на электроны, чем на атомные ядра, так как масса ядра во много раз больше массы электрона. Переменное поле волны вынужда­ет электроны в атомах и молекулах вещества совершать колебания с частотой волны ω. Колеблющиеся электроны сами излучают электро­магнитные волны, частота которых равна частоте колебаний электронов. Таким образом, падающая на вещество волна принуждает само вещество испускать волны той же частоты. Причем испускаемые веществом вол­ны распространяются во всех направлениях. Некоторые из них движут­ся навстречу падающей волне. Это так называемые отраженные волны. Отраженная волна представляет собой суперпозицию волн, испущенных всеми атомами вещества. Но кажется, что падающая волна отражается от поверхности тела.

Точный расчет показателя преломления очень сложен. Поэтому в этой главе будет изложена теория дисперсии света, которая справед­лива только для веществ с показателем преломления, близким к еди­нице. Такими показателями преломления характеризуются, например, разреженные газы. В этом случае излучение самого вещества является достаточно слабым и его можно не учитывать.

Прежде чем исследовать воздействие электромагнитной волны на ве­щество, необходимо представить себе строение молекул, из которых со­стоит это вещество. Каждая молекула состоит из одного или нескольких положительно заряженных ядер и определенного количества электронов. Так как масса ядер велика по сравнению с массой электронов, смеще­нием ядер можно пренебречь и считать, что подвижными частицами в молекуле являются только электроны. Электрон в молекуле удержи­вается в ее пределах некоторой силой. Самое простое выражение для такой силы имеет вид

F = -Kr, (15.2)

где r - радиус-вектор электрона; К - положительный коэффициент. Это есть центральная сила, притягивающая электрон к точке, в которой на­ходится начало его радиус-вектора. Предположим, что движение элек­трона в молекуле можно описать посредством второго закона Ньютона

т r''= F .

В проекциях на ось у закон Ньютона с учетом формулы (15.2) можно записать так:

m у''= - К у.

Это уравнение удобно преобразовать к виду

у'' + ω₀ ² у=0 (15.3)

где

ω₀ ² =K/m

(15.4)

Уравнение (15.3) есть дифференциальное уравнение гармонических ко­лебаний. Таким образом, согласно принятой модели электрон в молеку­ле совершает гармонические колебания с частотой ω₀ .

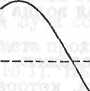
Рис. 15.2. Гармоническая волна вынуждает электрон в молекуле совершать колебания около положения равновесия

Пусть гармоническая линейно поляризованная электромагнитная вол­на распространяется вдоль оси х (рис. 15.2). Если вектор напряженно­сти электрического поля этой волны направлен по оси у, то такая волна будет описываться функцией

Е_у = Е_т cos (ω t - к х),

где Е_т - амплитуда волны, ω - ее частота.

На электрон, движущийся в электромагнитном поле со скоростью v, действует сила Лоренца

F = - е (E + [vB]) (15.6)

Найдем отношение модулей сил(15.10)

F_e = - е E, F_m =- е [vB])

с которыми на электрон действуют магнитное и электрическое поля вол­ны соответственно. С учетом соотношения (11.30) получим

F_m /F_e = v B_m/E_m, =vμH_m/E_m = v√με=v/c

где

c = 1/√με

- скорость света. Так как скорость электрона в молекуле существенно меньше скорости света, действием на него магнитного поля волны можно пренебречь.

Итак, на электрон в молекуле, на которую падает электромагнитная волна, будут действовать две силы. Первая сила удерживает электрон в пределах¹ молекулы, а вторая есть сила, с которой на него действу­ет электрическое поле волны. Рассматриваемая молекула находится в начале координат. Поэтому проекция электрической силы на ось у будет

F_y = -e E_y(t, x = 0) = - е Е_т cos ωt. (15.7)

При этом второй закон Ньютона в проекциях на ось у будет иметь вид

ту'' = К у- е Е_т cos ωt.

Запишем это (15.8)уравнение так:

у'' + ω₀² у =( е Е_т/m) cos ωt (15.9)

Частное решение полученного уравнения, описывающее вынужденные колебания электрона под действием электромагнитной волны, есть гар­моническая функция с частотой волны:

y(t) = A cosωt, (15.10)

где А - амплитуда вынужденных колебаний. Подставив эту функцию в уравнение (15.9), найдем амплитуду колебаний электрона в молекуле под действием переменного электрического поля волны:

A = е Е_т/(m(ω²-ω₀²)) (15.11)

Согласно этой формуле в том случае, когда частота волны ω равна ча­стоте ω₀ собственных колебаний электрона, амплитуда его вынужденных колебаний становится бесконечно большой. Очевидно, что в действи­тельности так быть не может. Однако продолжим вычисления.

Подставим выражение (15.11) в формулу (15.10). Получим следующую зависимость:

y(t) = ( е /(m(ω²-ω₀²))E_y(t). (15.12)

Как видно из этой формулы, под действием электрического поля волны электрон в молекуле смещается из положения равновесия вдоль напра­вления вектора напряженности электрического поля. Векторной форме формула (15.12) имеет вид

r(t) = ( е /(m(ω²-ω₀²))E(t). (15.13)

Смещения электронов в молекуле из положений равновесия приво­дят к ее поляризации. Степень поляризации молекулы характеризуется электрическим дипольным моментом

(15.14)

где r_i - радиус-вектор одного из электронов под номером i. Смещение электрона под действием электрического поля волны описывается фор­мулой (15.13). Таким образом, для дипольного момента молекулы можно записать следующее выражение:

(15.15)

где ω_0i - частота собственных колебаний i-го электрона в молекуле. При­чем эта формула справедлива для любой молекулы вещества, где бы она ни находилась.

Если все молекулы вещества одинаковы, то поляризованность веще­ства, т.е. дипольный момент единицы объема, будет равен произведению дипольного момента одной молекулы на их концентрацию:

Р =пр.

Как видно из формул (15.15) и (15.16), вектор Р поляризованности веще­ства коллинеарен вектору Е напряженности электрического поля, т.е. справедливо соотношение (2.24)

Р = ε_оχ_еЕ ,

из которого найдем диэлектрическую восприимчивость вещества χ_е. Затем по формуле (2.27) найдем относительную диэлектрическую проницаемость:

ε_r = 1 +χ_е

В результате придем к формуле

(15.17)

Показатель преломления связан с относительной проницаемостью веще­ства соотношением (11.38)

n=√ε_r (15.18

Формулы (15.17) и (15.18) определяют искомую зависимость показателя преломления вещества от частоты электромагнитного излучения. Гра­фик этой зависимости показан на рис. 15.3 для случая, когда частота собственных колебаний электронов принимает только два значения ω₀₁ ,ω₀₂

Рис. 15.3. Идеализированная зависимость показателя преломления от частоты электромагнитного излучения

Для всех прозрачных веществ частоты собственных колебаний элек­тронов в атомах и молекулах больше частот видимого электромагнитного излучения. Так, например, для воздуха и многих других газов частоты собственных колебаний электронов соответствуют частотам ультрафио­летового излучения. Таким образом, для этих веществ в видимой части спектра ω < ω_0i. Как видно из графика на рис. 15.3, при этих частотах показатель преломления будет больше единицы и является монотонно возрастающей функцией частоты ω. Частота фиолетового света больше, чем частота красного. Поэтому и показатель преломления фиолетового света больше, чем красного. По этой причине лучи фиолетового света отклоняются призмой сильнее, чем лучи красного света (рис. 15.1).

Развитая теория имеет существенный недостаток. Согласно этой те­ории в том случае, когда частота ω падающего на вещество излучения приближается к одной из частот ω₀₁ собственных колебаний электронов, показатель преломления вещества стремится к ±оо. Разумеется, этот вывод теории лишен физического смысла. Указанный недостаток теории может быть исправлен, если учесть, что свободные колебания электро­нов должны быть затухающими, т.е. электрон, совершающий свободные колебания, должен постепенно терять свою энергию. В таком случае

291

амплитуда вынужденных колебаний электрона ни при каких частотах ω не будет бесконечной, а зависимость п = п(ω) показателя преломления от частоты волны будет подобна зависимости, график которой изобра­жен на рис, 15.4. Из этого рисунка видно, что при некоторых частотах функция

п = п(ω) является возрастающей. Такую дисперсию называ­ют нормальной. На тех частотных интервалах, где функция п = п(ω) убывает, дисперсию называют аномальной.

Рис. 15.4- Зависимость показателя преломления от частоты

По определению показатель преломления вещества есть отношение скорости света в вакууме с к скорости v электромагнитной волны в ве­ществе:

п=c/v. (15.19)

Изображенная на рис. 15.4 зависимость показателя преломления от ча­стоты такова, что при некоторых значениях частоты показатель прело­мления оказывается меньше единицы. Согласно формуле (15.19) волны с такими частотами распространяются в веществе со скоростью v, боль­шей скорости света в вакууме: v > с. Этот результат требует некоторых пояснений,