
- •Основные действия над матрицами
- •Операция умножения матриц
- •Транспонированная матрица
- •Определители.( детерминанты)
- •Обратная матрица
- •Cвойства обратных матриц
- •Ранг матрицы
- •Элементарные преобразования матрицы
- •Теорема о базисном миноре
- •Примеры
- •Свойства решений системы линейных уравнений
- •Фундаментальная система решений линейного однородного уравнения
- •Изменение матрицы линейного преобразования при изменении базиса
Изменение матрицы линейного преобразования при изменении базиса
В предыдущем разделе мы установили, что как только в линейном пространстве выбран базис, то каждому линейному преобразованию соответствует матрица этого преобразования. Однако если выбрать в пространстве другой базис, то матрица преобразования, как правило, станет другой. Выясним, как эти матрицы связаны между собой.
Пусть
--
-мерное
линейное пространство,
![]() и
и
![]() --
два базиса в этом пространстве. Первый
из них назовем "старым", а второй --
"новым". Пусть
--
два базиса в этом пространстве. Первый
из них назовем "старым", а второй --
"новым". Пусть
![]() --
матрица перехода 19.1.4 а от старого базиса
к новому.
--
матрица перехода 19.1.4 а от старого базиса
к новому.
Предложение
19.1 Пусть
![]() --
линейное преобразование пространства
,
--
линейное преобразование пространства
,
![]() и
и
![]() --
матрицы этого преобразования в старом
и новом базисе соответственно. Тогда
--
матрицы этого преобразования в старом
и новом базисе соответственно. Тогда
![]()
Доказательство.
Пусть
![]() --
произвольный вектор пространства
,
--
произвольный вектор пространства
,
![]() --
его образ, то есть
--
его образ, то есть
![]() .
Пусть
.
Пусть
![]() и
и
![]() --
координатные столбцы векторов
и
в
старом базисе, а
--
координатные столбцы векторов
и
в
старом базисе, а
![]() ,
,
![]() --
в новом. Тогда в силу формулы (19.3)
--
в новом. Тогда в силу формулы (19.3)
![]() .
По предложению
18.5 имеем
.
По предложению
18.5 имеем
![]() ,
,
![]() .
Подставим эти выражения в предыдущую
формулу, получаем
.
Подставим эти выражения в предыдущую
формулу, получаем
![]() .
Откуда
.
Откуда
![]() .
С другой стороны, в силу формулы (19.3)
в новом базисе
.
С другой стороны, в силу формулы (19.3)
в новом базисе
![]() .
Сравнивая это равенство с предыдущим,
получаем
.
Сравнивая это равенство с предыдущим,
получаем
![]() .
.
Определение
19.2 Две квадратных
матрицы
![]() и
и
![]() одного
порядка называются подобными, если
существует такая невырожденная матрица
,
что
одного
порядка называются подобными, если
существует такая невырожденная матрица
,
что
![]() .
.
Следствие 19.1 Матрицы одного линейного преобразования, соответствующие разным базисам, подобны друг другу, и наоборот, если матрицы подобны, то они являются матрицами одного и того же преобразования в разных базисах.
30
Напомним,
что в евклидовом пространстве определено
скалярное произведение векторов
![]()
Определение.
Если существует
такой оператор B,
что для любых
![]() и
и
![]() из
евклидова пространства E справедливо
из
евклидова пространства E справедливо
![]() ,
то оператор B
называется сопряженным оператором к
оператору A
и обозначается A*:
,
то оператор B
называется сопряженным оператором к
оператору A
и обозначается A*:
![]()
Теорема. Если A — линейный оператор в евклидовом пространстве E и A — его матрица в некотором ортонормированном базисе в E, то у оператора есть единственный сопряженный оператор, причем матрица сопряженного оператора в том же базисе — это матрица AT.
Теорема доказана на лекции.
Пример. Рассмотрим оператор U поворота пространства R2 на угол относительно начала координат против часовой стрелки:
![]()
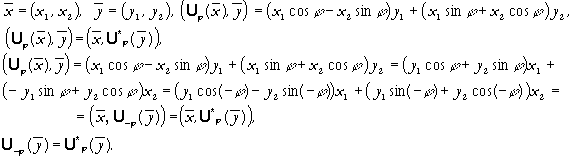 Т.е.
оператор, сопряженный оператору поворота
пространства R2
на угол
относительно начала координат против
часовой стрелки — оператор
поворота пространства R2
на угол -
относительно начала координат против
часовой стрелки.
Т.е.
оператор, сопряженный оператору поворота
пространства R2
на угол
относительно начала координат против
часовой стрелки — оператор
поворота пространства R2
на угол -
относительно начала координат против
часовой стрелки.
Матрицы операторов поворота на угол и угол - имеют, соответственно, вид:
![]() Видно,
что
Видно,
что
![]()
Нетрудно доказать (на лекции доказано) следующие свойства сопряженного оператора:
что сопряженный к линейному оператру — линейный оператор;
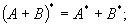
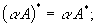
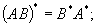
характеристические многочлены операторов
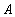 и
и
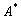
совпадают.
5.3.2. Самосопряженный оператор
Определение.
Если линейный
оператор A,
действующий в евклидовом пространсте
E,
таков, что для любых
и
из
E справедливо
![]() ,
то оператор A
называется самосопряженным оператором.
,
то оператор A
называется самосопряженным оператором.
Пример.
Оператор P2
— оператор проектирования пространства
R3
на подпространство R2
параллельно вектору
![]() :
:
![]() .
.
Как
показано выше, матрица оператора P2
в естественном
ортонормированном базисе
![]()
Имеет вид
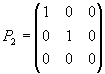
Тогда
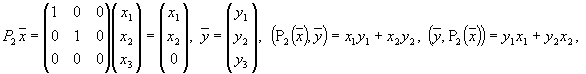 т.е.
т.е.
![]() —
оператор P2
— самосопряженный
оператор.
—
оператор P2
— самосопряженный
оператор.
Видно, что матрица P2 оператора P2 — симметричная матрица.
Нетрудно доказать следующие свойства самосопряженного оператора:
сумма самосопряженных операторов — самосопряженный оператор;
если оператор A самосопряженный оператор, то оператор
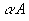 —
тоже самосопряженный оператор (
—
тоже самосопряженный оператор (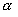 —
действительное число).
—
действительное число).
5.3.3. Собственные значения и собственные векторы самосопряженного оператора
Можно показать (на лекции не доказывается), что у самосопряженного оператора существует собственный ортонормированный базис.
Поскольку A=A*, то матрица самосопряженного оператора — симметричная матрица. Справедлива следующая теорема.
Теорема. Матрица самосопряженного оператора в собственном базисе имеет диагональную форму.
Ясно, что для того чтобы привести матрицу самосопряженного оператор к диагональному виду нужно найти собственные значения оператора и диагональную матрицу, на диагонали которой расположены собственные значения матрицы.
Если
нужно записать выражение для приведения
матрицы к этой диагональной форме, то
нужно еще найти собственные векторы
матрицы, записать матрицу C
перехода к собственному
базису (матрицу, столбцами которой
являются координаты собственных векторов
оператора), найти обратную к ней матрицу
С-1
и тогда
![]() —
равенство, связывающее диагональну
форму
—
равенство, связывающее диагональну
форму
![]() матрицы
оператора в собственном базисе с матрицей
A оператора
в заданном базисе.
матрицы
оператора в собственном базисе с матрицей
A оператора
в заданном базисе.
