Билет 17 (Методы проецирования. Центральное и параллельное проецирование. Основные свойства проекций.)

То же самое что и в первом билете.

свойства проекций.

1.Проеция вектора   на ось l равна произведению модуля вектора  на косинус угла между вектором и осью:

Доказательство. Ясно, что проекция вектора не изменится при его параллельном переносе, поэтому достаточно рассмотреть случай, когда начало вектора совпадает с началом отсчёта O оси l. Так как координата проекции начала равна нулю, то обозначим  .

Если угол φ острый, то из прямоугольного   получаем  . Откуда   или 

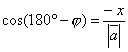Если угол φ тупой, то x< 0,  . Тогда из     или  . Т.е.  .

2.Проекция суммы двух векторов на ось равна сумме проекций векторов на ту же ось:  .

Доказательство. Пусть  . Обозначим через x1, x2 и x3 координаты проекций A1, B1, C1 на ось l точек A, B и C. Тогда  . Но  .

Это свойство можно обобщить на случай любого числа слагаемых.

3.Если вектор   умножается на число λ, то его проекция на ось также умножается на это число:

.

Доказательство. Пусть угол между вектором   и осью  .

Если λ > 0, то вектор   имеет то же направление, что и  , и составляет с осью такой же угол  .

При λ > 0  .

Если же λ < 0, то   и   имеют противоположные направления и вектор   составляет с осью угол π – φ и  .

Следствие. Проекция разности двух векторов на ось равна разности проекций этих векторов на ту же ось.

Билет 18 (Следы прямой. Следы плоскости.)

След прямой – точка, в которой прямая пересекается с плоскостью проекций.

Так как след принадлежит одной из плоскостей одна из его координат равна нулю:

У горизонтального следа координата z равна нулю.

У фронтального координата y.

У профильного x.

А прямая общего положения может пересекать все 3 плоскости.

Правила построения следов на эпюре:

1. Для построения горизонтального следа прямой необходимо продолжить ее фронтальную проекцию до пересечения с осью Х и в этой точке восставить к оси перпендикуляр до пересечения с горизонтальной проекцией прямой.

2. Для построения фронтального следа прямой нужно из точки пересечения горизонтальной проекции ее с осью Х восставить перпендикуляр к оси пересечения с фронтальной проекцией прямой.

Видимой частью прямой будет та, которая расположена в пределах первого октанта.

След плоскости – прямая линия, по которой данная плоскость пересекается с плоскостями проекций.

Плоскость общего положения имеет 3 следа: горизонтальный (пересечение с П₁), фронтальный (пересечение с П₂) и профильный (пересечение с П₃).

Каждый из следов совпадает со своей одноименной проекцией, а две другие – разноименные проекции – оказываются лежащими на осях.

Билет 19 (Параллельные плоскости. Прямая параллельная плоскости.)

Плоскости параллельны, если 2 пересекающиеся прямые одной плоскости соответственно параллельны двум пересекающимся прямым другой плоскости.

Прямая перпендикулярна плоскости, если она перпендикулярна одной из прямых, лежащих в этой плоскости.

Билет 20 (Определение истинной величины отрезка прямой и углов наклона к плоскостям п1 и п2 методом перемены плоскостей проекций.)

На рис. 5.1 показано преобразование проекций точки А из системы П₂⁄П₁ в систему S⁄П₁, в которой вместо плоскости П₂ введена новая плоскость S, а плоскость П₁ осталась неизменной. При этом S перпендикулярна П₁ . В системе S⁄П₁горизонтальная проекция a точки A осталась неизменной . Проекция a_s точки A на плоскости S находится от плоскости П₁ на том же расстоянии, что и проекция a₂ точки А на плоскости П₂. Это условие позволяет легко строить проекцию точки на чертеже новой плоскости проекций. Для этого в новой системе (П₁⁄S) из проекции точки (a) на сохраняющейся плоскости проекций проводят линию связи, перпендикулярную к новой оси проекций (S / П₁) . На этой линии связи отмечают расстояние от оси П₁ / S до проекции a_s точки на новой плоскости проекций S, равное расстоянию от преобразуемой проекции точки a₂ до оси проекций П₂/ П₁ в системе П₂[П₁ ( | a_s-a_x1| =| a₂- a_x | ).