
- •Тема 2 . «основные виды топлив применяемых в рдтт».
- •Основные закономерности горения баллиститных топлив.
- •Влияние давления на скорость горения.
- •Влияние внешней температуры на скорость горения твердого топлива.
- •Эрозионное горение твердого топлива.
- •Определение скорости горения.
- •Особенности горения смесевых и металлизированных топлив рдтт.
- •Тема 4. Основные уравнения внутренней баллистики рдтт. (44)
- •Тема 5 Основные типы зарядов рдтт и методы расчета выгорания зарядов (2ч).
- •Тема 6 : газодинамический расчет внутри камерных процессах в рдтт.
- •Лекция 9
- •Тема 7. Течение продуктов сгорания в соплах рдтт.
- •Двухфазные эффекты
- •Лекция 10 Профилирование сопел рдтт.
- •Расчет потерь тяги и удельного импульса в соплах рдтт.
- •Потери из-за скоростного и температурного отставания.
- •Потери из-за осаждения
- •Потери из-за двухслойности.
- •Лекция №11
- •Активное регулирование тяги.
- •Пассивное (программное) регулирование тяги рдтт.
- •Рдтт многократного включения
- •Управление вектором тяги
- •Активное и пассивное включение рдтт
- •Лекция 12
- •Тема 9 : Нестационарные режимы работы рдтт
- •Особенности запуска рдтт
- •Выбор воспламенителя и метод расчёта его массы
- •Приближенный расчёт запуска рдтт
- •Расчёт переходных процессов в рдтт
Тема 4. Основные уравнения внутренней баллистики рдтт. (44)
-Расчет давления в камере сгорания в приближении сосредоточенных параметров;
-Устойчивость стационарного рабочего процесса в РДТТ;
-Расчет давления в камере сгорания РДТТ с учетом изменения параметров по тракту двигателя;
-Расчет тяги, удельного и суммарного импульса РДТТ;
-Разброс параметров РДТТ и методы компенсации разброса.
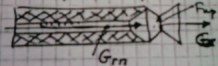
Расчет давления в камере сгорания в приближении сосредоточенных параметров.
Давление в камере сгорания Рк является определяющим при расчете других важных параметров.
Наиболее просто решается задача определения давления для стационарного режима работы, когда параметры равномерно распределены по всему объему камеры. Они сосредоточены в некоторой, отдельно взятой точке камеры и не изменяются при переходе в другую точку.
Любые локальные параметры в объеме – одинаковы и не зависят от расположения.
Считается, что скорость движения в камере равна нулю и справедливо соотношение: газоприход = расходу газа через сопло:

Из термодинамических расчетов для истечения через сопло известно:
 ,
,
где Рк - давление в камере [атм];
Fkp-площадь критического сечения [м2]
G-расход, [кг/c]
Термодинамический параметр β - расходный комплекс засчитывается как:
 ,
[c]
,
[c]
7.Для определения величины давления в камере сгорания запишем с учетом размерностей:


8.
Размерности : в - коэффициент,
 -_
_ _ _ _кг/м2;
Рк - кг/см2;
U – мм/с; Fкр-
ST;
-_
_ _ _ _кг/м2;
Рк - кг/см2;
U – мм/с; Fкр-
ST;
 -
_ _ _ с = _ _ _ _ м/с;
-
_ _ _ с = _ _ _ _ м/с; Тк
–К; g=9,81м
/с2.
Тк
–К; g=9,81м
/с2.
9. Получаем
 - уравнение
Бора
- уравнение
Бора
10.
Если считать, что в = const,
 для данного вида топлива, то параметр
для топлива …8 получаем:
для данного вида топлива, то параметр
для топлива …8 получаем:

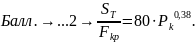
11.
Для определения величины давления по
геометрическим параметрам получаем
параметр для …8


Размерность
коэффициента такой же, как у
 .
.
12. Другими словами: все определяется отношением площадей поверхности горения и площади критического сечения сопла.
13. Термодинамические характеристики для продуктов сгорания различных топлив весьма консервативны и практически не изменяются в широком диапазоне.
Устойчивость стационарного процесса в РДТТ.
1. Устойчивость стационарного процесса – это такой режим горения, при котором при малых изменениях параметров, приводящих к относительных давлений, процесс горения не переходит в стадию неустойчивости.
2. Другими словами малые отклонения не растягивают процесс, а внутренние процессы приводят его в первоначальное стабильное состояние.
3. При обратном утверждении – процесс неустойчив.
4.Неустойчивость в РДТТ сопровождается колебаниями давления в камере сгорания, вибрациям, которые могут привести к разрушению двигателя.
Для ЖРД
 ;
;
 =
=
 ;
;
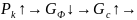 в
итоге падает давление
в
итоге падает давление
 ?
?
Для РДТТ
 ;
=
;
;
=
;

 в
итоге падает давление
в
итоге падает давление

Кривая выгорания соответствует кривой распределения температур:
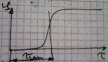
 -
время
запаздывания.
-
время
запаздывания.
Для
ЖРД более явно
 )
)


Бпсл -толщина прогретого спая.
5. Существуют два вида неустойчивости:
а) неустойчивость в отрасли низкого давления, при котором возникают колебания давления с частотой, близкой к собственной (акустической) частоте колебаний газа в камере сгорания.
б) акустическая неустойчивость, при которой возникают колебания давления с частотой , близкой к собственной(акустической) частоте колебаний газа в камере сгорания.
6. В настоящее время пополнен большой экспериментальный и теоретический материал по устойчивости: НО парного колебания пока нет.
7. Практически всегда теоретический анализ проводится в линейном приближении.
8. НО! Процессы в камере существенно нелинейные.
9. О стабильности горения можно судить по давлению Р(τ)


10. Линейное приближение предполагает мягкое возбуждение процесса неустойчивости.
11.
Как правило при линейном подходе
колебания синусоида

12. При нелинейном подходе – возбуждение жесткое колебания могут быть в виде солитонов .
Низкочастотная неустойчивость.
При давлении в камере ниже некоторой границы процесс работы РДТТ становится неустойчивым.
Давление падает – заряд загасает.
Заряд может воспламениться за счет акуммулированного конструкцией тепла и вновь загаснуть – аномальное горение.

Это связано с инерцией с инерцией прогретого спая при быстроменяющемся давлении в камере сгорания.
Низкочастотная неустойчивость поступает при условии
 -критическое
отношение времен
релаксации
камеры двигателя
-критическое
отношение времен
релаксации
камеры двигателя
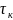 и времени релаксации прогретого спая
топлива
и времени релаксации прогретого спая
топлива
 .
.Эксперименты показывают, что для критических условий
 -
одного порядка.
-
одного порядка.В общем случае критическое отношение времен релаксации может быть найдено из системы нелинейных уравнений:
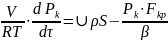 - уравнение
расхода ;
- уравнение
расхода ;
 - уравнение
энергии;
- уравнение
энергии;
7.К этим условия добавляются граничные условия.
8. Уравнения в общем виде связывают скорость горения и температуру поверхности.
9. Решается система численно.
10.
Вводится понятие малого отношения
параметра
 и далее вся математика сводится к
исследованию устойчивости в математической
модели.
и далее вся математика сводится к
исследованию устойчивости в математической
модели.
Дифференциальное уравнение →вводятся малые отклонения →исследование АФИХ
11.
Время релаксации камеры
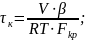 с точностью
20…30%
с точностью
20…30%
12.
Время релаксации прогретого спая
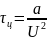 ,
, – может
изменяться в том же диапазоне более чем
на два порядка.
– может
изменяться в том же диапазоне более чем
на два порядка.
13. Физически: процесс низкочастотной неустойчивости возникает из-за несоизмеримости времен прогрева и движения газа в камеру сгорания.
14.
Линейное решение позволяет определить
отношение
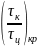 через
характеристики ТТ и конструктивные
параметры РДТТ и получить зависимость
предельного значения устойчивого
горения:
через
характеристики ТТ и конструктивные
параметры РДТТ и получить зависимость
предельного значения устойчивого
горения:
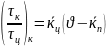 ,
,
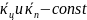 .
.
15.
из равенства
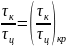 определяется
определяется
 ,
ниже которого находится неустойчивое
горение.
,
ниже которого находится неустойчивое
горение.
 .
.
16.
Если свободный объем это
 ,
то
,
то
 Lk
с учетом
ранее полученной формулы:
Lk
с учетом
ранее полученной формулы:
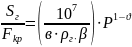 ,
получаем:
,
получаем:
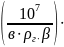 Lk
Lk

17. Собираем Рпр:

18.
Откуда Рпр=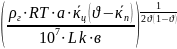 ,
,
Ниже этого значения будет неустойчивость.
19.
Время релаксации камеры:
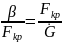 ;
;
 .
.
20.
 - время работы
двигателя.
- время работы
двигателя.
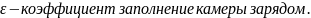
Акустическая неустойчивость.
1кГц
В камерах сгорания при их работе всегда имеются случайные колебания давления продуктов сгорания.
Эти колебания в РДТТ могут составлять 3%.
Акустическая неустойчивость горения - это автоколебательный процесс, в котором обратная связь, обеспечивающая необходимое для поддержания незатухающих волновых движений поступления энергии от непериодического источника тепла (процесс горения), осуществляется через воздействие звуковых волн на горение.
Параметры самих волновых движений: амплитуда, форма колебаний и частота определяются внутренними свойствами самой системы.
Звуковой шум в камерах сгорания также представляет автоколебательный процесс. Uст -горение + отр.св.звук
Для получения комплексных соотношении используется уравнение движения (Эйлера), энергии неразрывности и состояния .


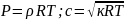 .
.
Вводим малые возмущения.
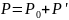 ;
V=
;
V= ;
…. Подставляем в уравнения и решаем.
;
…. Подставляем в уравнения и решаем.В случае однородной среды и отсутствия источников тепла преобразованного уравнения получаем волновое уравнение:
 .
.Для камеры цилиндрические формы закрытой с обоих торцов при простейших граничных условиях (недеформированной стали )решение имеет вид:
 (суммируем
по m,n,z)
m,n,z-целые
числа;
(суммируем
по m,n,z)
m,n,z-целые
числа;
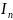 - функция Бесселя;
- функция Бесселя;

 *
*Здесь Г,R – текущий размер и радиус камеры сгорания. Х,L – текущая длина и длина камеры сгорания.
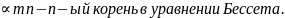
Члены с n=m=0 и z
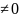 – продольные моды
– продольные моды
n=z=0 m - радиальные моды;
m=z=0 и n - тангенсальные моды;
Из * можно получить , что для коротких камер сгорания
 -
наиболее низкая частота соответствует
первой тангенсальной моде.
-
наиболее низкая частота соответствует
первой тангенсальной моде.
 – соответствует первой тангенсальной
моде. Для длинных камер
– соответствует первой тангенсальной
моде. Для длинных камер
 :
:
 -
соответствует
основной продольной моде.
-
соответствует
основной продольной моде.Если не учитывать взаимодействия звуковых волн с процессами горения, то в коротких камерах сгорания прежде всего должны возникать тангенсальные колебания ,а затем продольные, так как с увеличением частоты колебаний растут акустические потери.
Основные мероприятия по преодолению акустической неустойчивости.
Выбор формы топливного заряда, который может снизить неустойчивость.
Выбор оптимальной формы камеры сгорания, которая определяет частоту собственных колебаний.
Эффективное использование различных мероприятий , направленных на увеличение потерь колебательной энергии(резонансные поглотители, диафрагмы и т.п)
Важнейшим фактором увеличения рассматриваемых потерь является наличие n-форм.
Геометрия входной части сопла также влияет на акустическую усталостность.
Лекция 5
Расчет давления в камере с учетом изменения параметров по тракту двигателя.
От сложности профиля заряда существенно зависит статическое давление по длине.
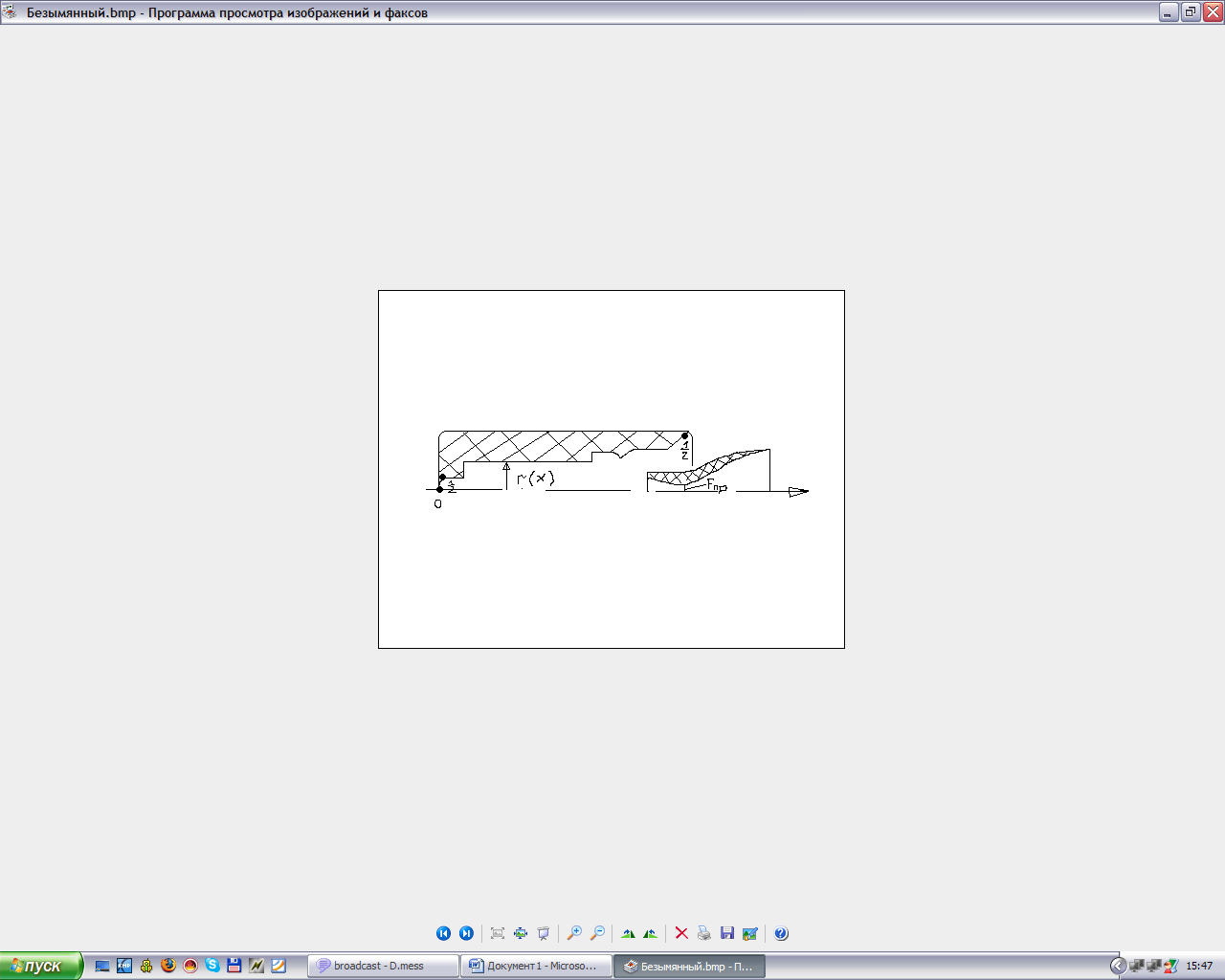
F
=
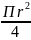 ; F(x)
Запои площади
; F(x)
Запои площади
2. Известны газодинамические функции давления и расхода.
 = (1-
= (1-
 *
* ;
;
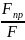 = (
= ( * (1-
*
* (1-
*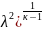 * λ;
* λ;
Здесь
 ,
,
 - статическое и полное давление;
- статическое и полное давление;
 ,
,
 - текущая площадь и критическая площадь
; к – показатель адиабаты и безразмерная
λ =
- текущая площадь и критическая площадь
; к – показатель адиабаты и безразмерная
λ =
 .
.
3. В момент тоже найдем соотношение
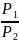 =
(
=
( *
*
 = [
*У*(
)
= [
*У*(
)
4. Найдем
У:
= (
* ( * λ1 откуда У = неявная зависимость
от
.
* λ1 откуда У = неявная зависимость
от
.
5. Таким образом, зная запои площади, в каждом сечении определяем статическое давление. Возможно определить Р = ƒ(х)
Потери полного давления по тракту камеры сгорания и каналу заряда.
1. Потери полного давления в камере сгорания и по каналу заряда определяются по аналогии с течением по тракту движения жидкости в трубе с преградами.
2. Считается справедливыми гидродинамические соотношения, полученные на воде и газах и выраженные в виде электрических зависимостей. Возможно в первом приближении использовать гидродинамический справочник Шдельгина.
Местные сопротивления.
1. Внезапное расширение потока приводит к потере полного давления:

Формула
Дарси-Вейсбаха Δ = ρ
= ρ
 =
=
 [1-(
[1-(
2. Другая
формула: ΔЕ = ξ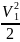 ,
ΔЕ – потеря кинетической энергии: после
преобразований
,
ΔЕ – потеря кинетической энергии: после
преобразований
 = 1- ξ
= 1- ξ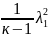 ;
ξ – коэффициент потерь посчитаной
таблицы.
;
ξ – коэффициент потерь посчитаной
таблицы.
3. Потери в цилиндрическом потоке:

U = U1РVУ(λ); λ – местная скорость газа.
Из гидравлики
известно: dLтр = ξ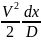 →можно получить→
→можно получить→ - 1)
- 1) =
=
 ξ
ξ .
.
Обычно пишут
Δ
=
 – формула трения.
– формула трения.
4.
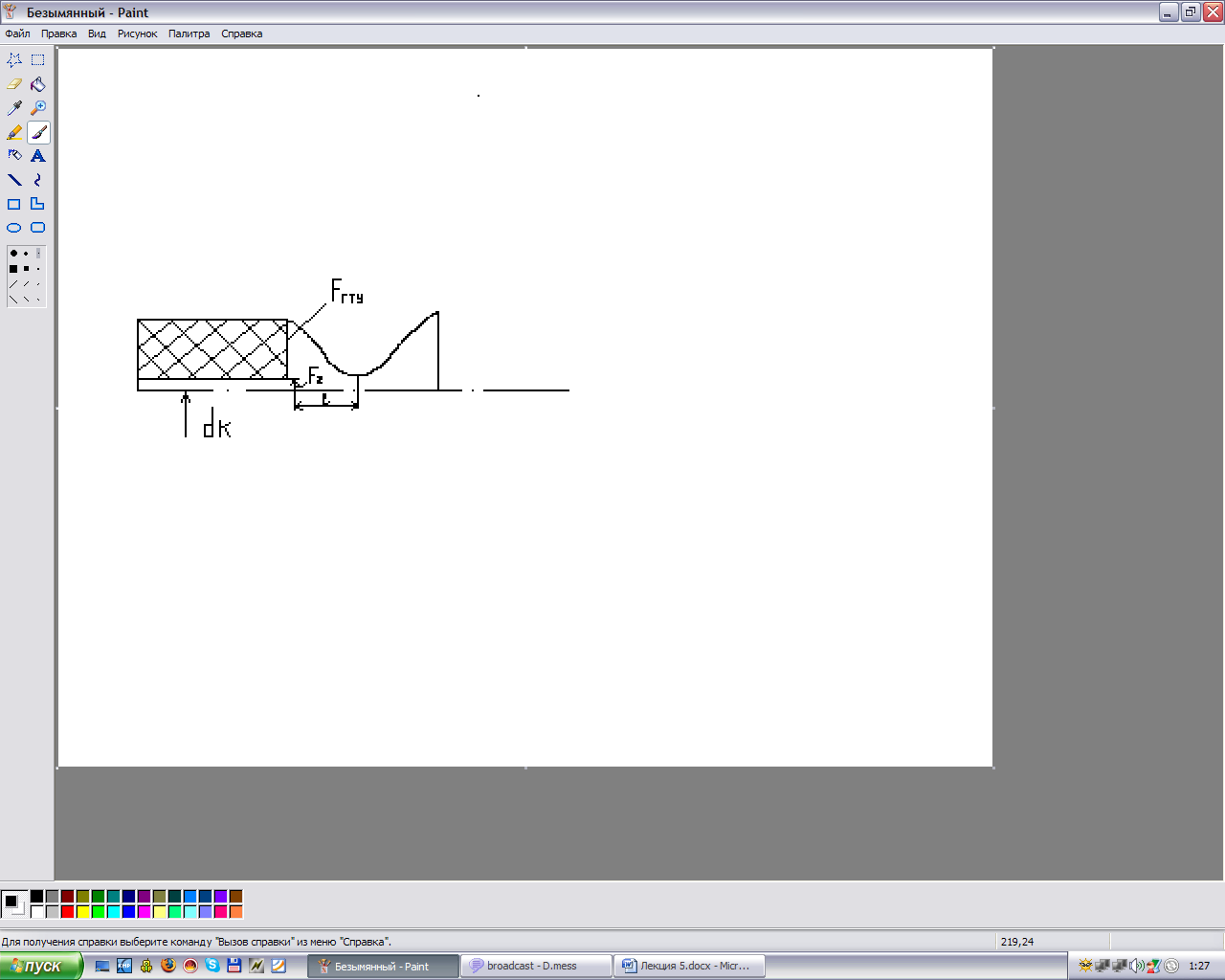
Потери в
предсопловом объеме: ξ = 0,15
 ;
;
5. Для q(λ) можно записать
q(λ2) =
 .
.
6. Слияние двух потоков:


Волна
Потери полного
давления могут быть определены по
аналогии → ξ
7. В итоге полное давление по длине падает. При этом энтропия возрастает
S2
– S1 = R
lnσ; σ =

Расчет тяги, удельного и суммарного импульса.
Тягой ракетного двигателя является равнодействующая всех сил, приложенных к нему во время его работы. Это внутренние силы продуктов сгорания и внешние со стороны окружающей среды.
Тяга определяется после интегрирования уравнения импульса в виде:
R = G*Wa+Pa*Fa – Pн*Fa = G*Wa+ Fa*(Pa – Pн);
Тяга в пустоте Pн = 0
Rп = G*Wa + Pa*Fa;
Тяга на расчетном режиме Pa = Pн
Rр = G*Wa ;
Тяга на высоте иногда записывается:
Rн = G*Wэф,
где Wэф
= Wa+ * Fa
* Fa
Удельный импульс тяги.
Это одно и то же, что удельная тяга Rуд.
Это основной параметр, характеризующий энергетику. Для пустоты:
Rуд
п =

Мт – масса топлива.
При постоянстве Pk(τ) = const и пр.
Запишем: Rуд
п =

G – расход.
Rуд п = Wa +
 = Wa
= Wa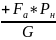 *
* ;
;
В критике
 =
=
 = 1 – очковое
сопло.
= 1 – очковое
сопло.
Тогда: Rуд
п кр = Wкр
+
 *Пкр
*Пкр
Rуд п кр = акр + β* Пкр
Wкр
= акр
=
 ;
β
=
;
β
=
 и Пкр
= (
и Пкр
= (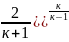
Частный случай:
Rуд
п кр = акр*(1+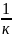 )
)
Rуд п кр = β*(к+2)* Пкр
Уравнение для пустотного удельного импульса тяги преобразует, домножив и поделив его на величину удельного импульса очкового импульса:
Rуд
п =

После преобразований получаем:
R уд
п = β*(к*Пкр*λа
+ Па*
уд
п = β*(к*Пкр*λа
+ Па* )
Обозначим ξ
=
)
Обозначим ξ
=
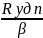
Аналогично можно получить:
ξ
=
; η
= ξ
=
 ;
θ = ξ
=
;
θ = ξ
=

[β]
= [ ]
= [
]
= [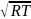 ]
=
]
=
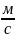
ξ,η и θ – газодинамические функции (Г/Д)

Функции ξ,η и θ – характеризуют сопло.
β, акр, - характеризуют камеру – (Т/Д)
Формулы с разделяющимися переменными зависящими только от камеры и только от сопла:
Rуд = ξ*β; Rуд = η* акр; Rуд = θ* .
Представление формул для удельного импульса тяги в таком виде удобно, например, при определении потерь удельного импульса, отдельно камерных и отдельно сопловых:
ζ
=

Суммарный импульс тяги.
Суммарный (для простоты пустотный) импульс определяется как интеграл тяги по времени:
IΣ
=

С учетом предыдущих выкладок (Rуд п = ξ*β)
IΣ
=

При ξ и Fкр = const
IΣ
= ξ
* Fкр * и его можно вычислить после интегрирования
кривой
и его можно вычислить после интегрирования
кривой
Можно записать и по другому для постоянных значений Rуд, то есть для IΣ ном
IΣ
ном = Rуд
ном* = Rуд
ном*Мт
= Rуд
ном*Мт
По отношению к номинальному суммарному импульсу можно судить об эффективности заряда твердого топлива.
IΣ
= IΣ
ном*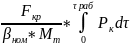
ном. – номинальное, заданное в ТЗ
Разброс параметров РДТТ и методы компенсации разброса.
Как видно из предыдущих выкладок о разбросе параметров РДТТ можно судить по разбросам значений давления в камере сгорания. И тягу и суммарный импульс тяги и расход и другие параметры можно выразить через давление в камере Рк.
ВБХ РДТТ в различных условиях имеют заметные отличия из-за разброса геометрических характеристик, типичных свойств, начальных температур зарядов и др.
Практически важным является уровень предельных отклонений, который влияет на надежность.
Выполняя зависимость
Рк
= (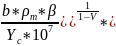
Прологарифмируем эту зависимость
lnPk
=

Возьмем от Рк логарифмическую производную и построим вручную в виде относительных приращений. Здесь Yc – коэффициент сопла.
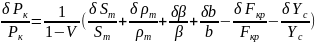
Полученные относительные разбросы характеризуют в соответствии с правилами теории вероятностей, можно записать через среднеквадратическое отклонение (СКО)
S δ:

По среднеквадратическому отклонению и аппарату теории вероятности можно вычислить и другие параметры, необходимые для надежности РДТТ.
Об этом подробно вам будут читать лекции на 5м курсе.
Лекция 6
